lc1215——来讨论一个数位dp解法！

Posted 2021-07-09 hans774882968

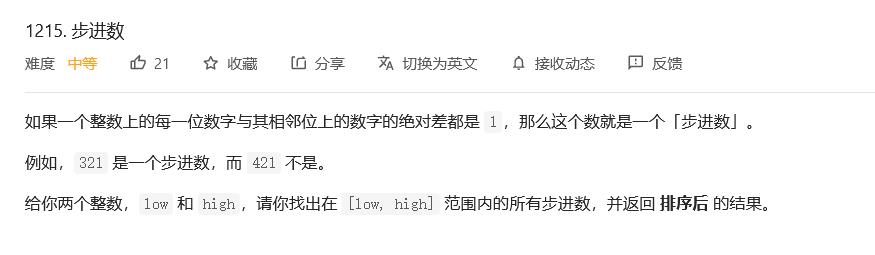
非常水，直接暴力判定即可。但如果把题目改成：求1e18范围内的“步进数”个数，则可以数位dp。数位dp思路和loj10164、loj10165很像，考虑上一位，在已知的数位dp的dfs模板上面修改即可。

dp[idx,i]记录的是恰好是idx+1位数（即没有前导0，且范围为10……0~99……9），且上一个数选择了i的答案。因此要引用dp或修改dp的时候，要保证“!isup && !zero”成立。前者保证范围上限达到99……9，后者保证当前没有前导0干扰。具体的dfs看代码叭。

由于这题是会猿题，所以只好本地对拍了QAQ。部分测试数据

1 7
1 8
1 9
1 10
1 20
1 90
1 91
1 1001
27 1002
1980 2120
12 200010
13 200010
12 200009
15416 159641
32626 54615
16427 33313
126649 213418
10 213417

代码（如果有错，请指出QAQ）

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
#define rep(i,a,b) for(int i = (a);i <= (b);++i)
#define re_(i,a,b) for(int i = (a);i < (b);++i)
#define dwn(i,a,b) for(int i = (a);i >= (b);--i)

const int SZ = 22;

int dl,d[SZ];LL dp[SZ][11];

template<typename Type>inline void read(Type &xx){
    Type f = 1;char ch;xx = 0;
    for(ch = getchar();ch < '0' || ch > '9';ch = getchar()) if(ch == '-') f = -1;
    for(;ch >= '0' && ch <= '9';ch = getchar()) xx = xx * 10 + ch - '0';
    xx *= f;
}

LL dfs(int idx,int las,bool isup,bool zero){
    if(idx == -1) return 1;
    if(!isup && !zero && ~dp[idx][las]) return dp[idx][las];
    int up = isup ? d[idx] : 9;
    LL ans = 0;
    rep(i,0,up){
        if(!zero && abs(i-las) != 1) continue;
        ans += dfs(idx-1,i,isup && i == up,zero && i == 0);
    }
    if(!isup && !zero) dp[idx][las] = ans;
    return ans;
}

LL solve(LL x){
    dl = 0;
    for(;x;x /= 10) d[dl++] = x % 10;
    return dfs(dl-1,0,true,true);
}

int bf(int a,int b){
    int ans = 0;
    vector<int> anss;
    rep(i,a,b){
        vector<int> d;
        for(int t = i;t;t /= 10) d.push_back(t % 10);
        bool fl = true;
        re_(j,0,int(d.size()) - 1){
            if(abs(d[j] - d[j+1]) != 1) fl = false;
        }
        if(fl) ++ans,anss.push_back(i);
    }
    if(ans <= 50){
        for(int &x: anss) cout << x << " ";
        puts("");
    }
    return ans;
}

int main(int argc, char** argv) {
    memset(dp,-1,sizeof dp);
    LL a,b;
    while(~scanf("%lld%lld",&a,&b)){
        LL ans = solve(b) - solve(a - 1);
        printf("%lld\\n",ans);
        int ans0 = bf(a,b);
        cout << ans0 << endl;//dbg
        assert(ans == ans0);
    }
    return 0;
}