第二篇：n-gram 语言模型

Posted 2021-07-08 flying_1314

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第二篇：n-gram 语言模型相关的知识，希望对你有一定的参考价值。

推到n-gram语言模型

平滑处理稀疏性

生成语言

推到n-gram语言模型

我们的目标是获得任意 m 个单词序列的概率:

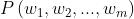
$P\\left ( w_{_{1}},w_{_{2}},...,w_{_{m}} \\right )$

第一步：应用链式法则将联合概率转换为条件概率

$P\\left ( w_{_{1}},w_{_{2}},...,w_{_{m}} \\right ) = P\\left ( w{_{1}}\\right )P\\left ( w{_{2}}\\right|w{_{1}} ) P\\left ( w{_{3}}\\right|w{_{1}},w{_{2}} ) ...P\\left ( w{_{m}}\\right|w{_{1}},w{_{2}},..., w{_{m-1}} )$

通过上面的转换，我们发现仍然很难去处理。因此我们做出简化的假设，也就是马尔可夫假设

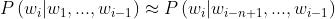
$P\\left ( w_{_{i}}|w_{_{1}},...,w_{_{i-1}} \\right ) \\approx P\\left ( w_{_{i}}|w_{_{i-n+1}},...,w_{_{i-1}} \\right )$

这个转换也就是，第i个单词不用依赖于前面所有词，而是依赖于前面n个词。这也就是我们今天所说的n-gram模型。

接下来，我们需要思考如何来计算这些概率？根据我们语料库中的计数进行估计

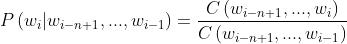
$P\\left ( w_{_{i}}|w_{_{i-n+1}},...,w_{_{i-1}} \\right ) = \\frac{C\\left ( w_{_{i-n+1}},...,w_{_{i}}\\right )}{C\\left ( w_{_{i-n+1}},...,w_{_{i-1}}\\right )}$

上面公式中的C指的就是出现次数。分子是从i-n+1到i这些词同时在语料库中出现的次数；分母是从i-n+1到i-1这些词同时出现在语料库中的次数。

然后，需要引入一个用于表示序列开始和结束的特殊标签：
使用<s> 表示句子开始；</s> 表示句子结束。

n-gram当然也存在一些问题，从公式出发，如果某一项的词并不在语料库中，会导致该项的概率为0并且，整体概率为0，该如何处理？

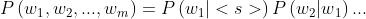
$P\\left ( w{_{1}},w{_{2}},...,w{_{m}}\\right ) = P\\left ( w{_{1}}|<s>\\right )P\\left ( w{_{2}}|w{_{1}}\\right )...$

比如w2在语料库中未出现，因此C(w2) =0 所以该项的概率为0，整体概率也为0，但是我们需要去用概率值和其他的可能的句子比较，如果多个句子都是等于0，就无法比较。

此时需要用到平滑，也就是接下来的部分。

平滑处理稀疏性

有很多种平滑处理的方法，此处主要对四种进行列举分析：

拉普拉斯平滑,也叫加1平滑
加k平滑
absolute discounting
Kneser-Ney

拉普拉斯平滑

简单的想法：假设我们看到的每个 n-gram 都多一次。下面公式中|V|是词表大小

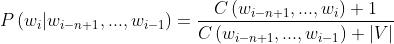
$P\\left ( w_{_{i}}|w_{_{i-n+1}},...,w_{_{i-1}} \\right ) = \\frac{C\\left ( w_{_{i-n+1}},...,w_{_{i}}\\right )+1}{C\\left ( w_{_{i-n+1}},...,w_{_{i-1}}\\right )+|V|}$

加k平滑（Lidstone Smoothing）

与上面类似，发现添加1个往往太多，因此添加一个分数 k

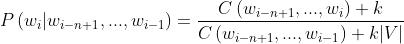
$P\\left ( w_{_{i}}|w_{_{i-n+1}},...,w_{_{i-1}} \\right ) = \\frac{C\\left ( w_{_{i-n+1}},...,w_{_{i}}\\right )+k}{C\\left ( w_{_{i-n+1}},...,w_{_{i-1}}\\right )+k|V|}$

但是这个k得人为指定，比如0.1等

absolute discounting

和上面的算法类似，不过是通过从观察到的 n-gram 计数中“借用”一个固定的概率质量
并将其重新分配到看不见的 n-gram。也就是给有概率的n-gram打折，折扣加到概率为0的n-gram上。

这里面提到一个概念叫back-off，回退，也就是说如果在高阶模型中没有该n-gram出现，可以尝试换到低阶模型，举例来说就是，3-gram回退到2-gram。这是一个简单整体理解

Kneser-Ney

基于低阶 n-gram 的通用性重新分配概率质量。也就是，持续性概率，continuation probability。

这里的通用性指的是：

高通用性:和很多其他单词一起出现。比如 glasses
低通用性：几乎不和其他单词一起出现，比如 francisco

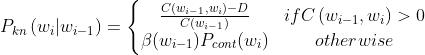
$P_{_{kn}}\\left ( w_{_{i}}|w_{_{i-1}}\\right ) = \\left\\{\\begin{matrix} \\frac{C \\left (w_{i-1}, w_{i}\\right )-D}{C \\left (w_{i-1}\\right )} & if C \\left (w_{i-1}, w_{i}\\right )>0 \\\\ \\beta(w_{i-1})P_{cont}(w_{i}) & otherwise \\end{matrix}\\right.$

这里的β表示已为上下文 wi-1 打折的概率质量的数量；

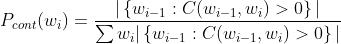
$P_{cont}(w_{i}) = \\frac{|\\left \\{w_{i-1}: C(w_{i-1},w_{i})>0 \\right \\}|}{\\sum w_{i} |\\left \\{w_{i-1}: C(w_{i-1},w_{i})>0 \\right \\}| }$

直观地，Pcont 的分子部分计算的是与 wi 共同出现的唯一 wi-1 的数量。

Interpolation 插补法

这里引入插补法，是组合不同阶n-gram模型的更好方法。

插补法结合刚刚的KN算法

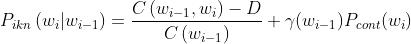
$P_{_{ikn}}\\left ( w_{_{i}}|w_{_{i-1}}\\right ) = \\frac{C \\left (w_{i-1}, w_{i}\\right )-D}{C \\left (w_{i-1}\\right )} +\\gamma (w_{i-1})P_{cont}(w_{i})$

这里γ指的是归一化常数，使得概率和为1

生成语言

给定一个初始词，根据语言模型产生的概率分布绘制下一个词。

这个其实比较好理解，给出<s>句子开始然后，假设使用bi-gram然后不断预测下一个词，直到预测到</s>

挑选下一个词有大概3种方法：

argmax：每回合取概率最高的词
贪心搜索
Beam搜索解码之后会讲：
每回合跟踪前 N 个概率最高的单词
选择产生最佳句子概率的单词序列
从分布中随机抽取

本次关于n-gram的模型讲解大概就是这样，这个算法还是比较实用的，辛苦大家观看，老规矩，有问题欢迎评论，探讨。

以上是关于第二篇：n-gram 语言模型的主要内容，如果未能解决你的问题，请参考以下文章