python快速幂算法解决大数取模
Posted Afololer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python快速幂算法解决大数取模相关的知识,希望对你有一定的参考价值。
1、前置性质
模运算的性质 [(a mod n)×(b mod n)] mod n = (a×b) mod n
指数可以拆分成二进制的形式,如9拆分成 1001
根据二进制的计算,1001 = ((1*2+0) *2 +0) *2+1 = 9
2、例子
那么5^9 mod 8 的计算可以分解为
5^1 mod 8 * 5 ^1 mod 8 * 5^2 mod 8 * 5^4 mod 8 * 5^1 mod 8
初始化d为0 意为5^0 每n轮计算的d为5^(n/2)次方
算5^1 mod 8 时 因为这时候9转化为2进制最高位为1
5^1 mod 8 = dxd mod 8 * d*a mod 8
算5^2 mod 8 时 这时候取第二位 0
5^2 mod 8 = dxd mod 8 d*a mod 8(因为是0,不用计算)
3、python代码实现
def tobinary(a): #转化为二进制
d = []
c = a
while(c!=0):
b = c % 2
c = int(c/2)
d.append(b)
return d
def quickmi(m,e,n): #快速幂算法
f = tobinary(e)
c = 0
d = 1
while(c!=e):
c = 2*c
d = (d*d)%n
g = f.pop()
if(g ==1):
c=c+1
d=(d*m)%n
return d
python内置的pow也可以实现大数幂取膜
4、测试用例
print(quickmi(1612050119,1757316971,5515596313))
print(pow(1612050119,1757316971,5515596313))
输出结果
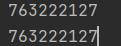
以上是关于python快速幂算法解决大数取模的主要内容,如果未能解决你的问题,请参考以下文章