一位被信号与系统耽误了的漫画家
Posted 卓晴
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一位被信号与系统耽误了的漫画家相关的知识,希望对你有一定的参考价值。

简 介: 本文介绍了本学期(2021-春季学期)信号与系统课程中有同学提交的一个漫画作品,利用动画来诠释卷积的物理过程。
关键词: 信号与系统,卷积,动画,漫画
今天收到了一份特殊的课程综合小论文作品,这是信号与系统分析课程兰弘博同学提交的一份用于动画作品,通过漫画的手法来阐述线性是不变系统在时域分析中的一个重要的公式: 卷积运算公式 。
对于一个线性时不变系统,它的零状态响应 y ( t ) y\\left( t \\right) y(t)等于系统的单位冲激响应 h ( t ) h\\left( t \\right) h(t)与输入信号 x ( t ) x\\left( t \\right) x(t)的卷积(convolve)。
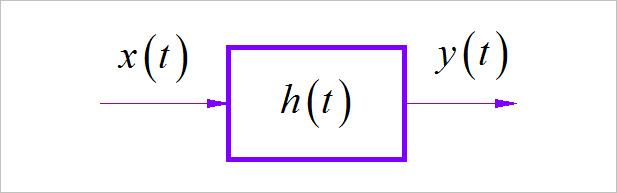
下面是卷积运算的数学定义。相比于信号的加、乘、微分、积分等操作,卷积是一个复杂的运算。其中卷积运算的“卷”来自于积分号中信号 h ( τ ) h\\left( \\tau \\right) h(τ)相对于积分变量 τ \\tau τ的反褶。
y ( t ) = ∫ − ∞ ∞ x ( τ ) ⋅ h ( t − τ ) d τ y\\left( t \\right) = \\int_{ - \\infty }^\\infty {x\\left( \\tau \\right) \\cdot h\\left( {t - \\tau } \\right)d\\tau } y(t)=∫−∞∞x(τ)⋅h(t−τ)dτ
本来十分严肃,堂堂正正的卷积运算在兰弘博手里则变成了一团随时被系统碾压的“面团”,到底输出是面条或是大饼取决于系统特性。

当然,要理解这坨面团如何被加工的,需要用到信号与系统江湖上的一门绝技-分身大法。 利用这分身术,无论面团起初是什么形状,它都可以被分解成薄厚均匀的冲激信号,只是冲激信号的面积不同而已。
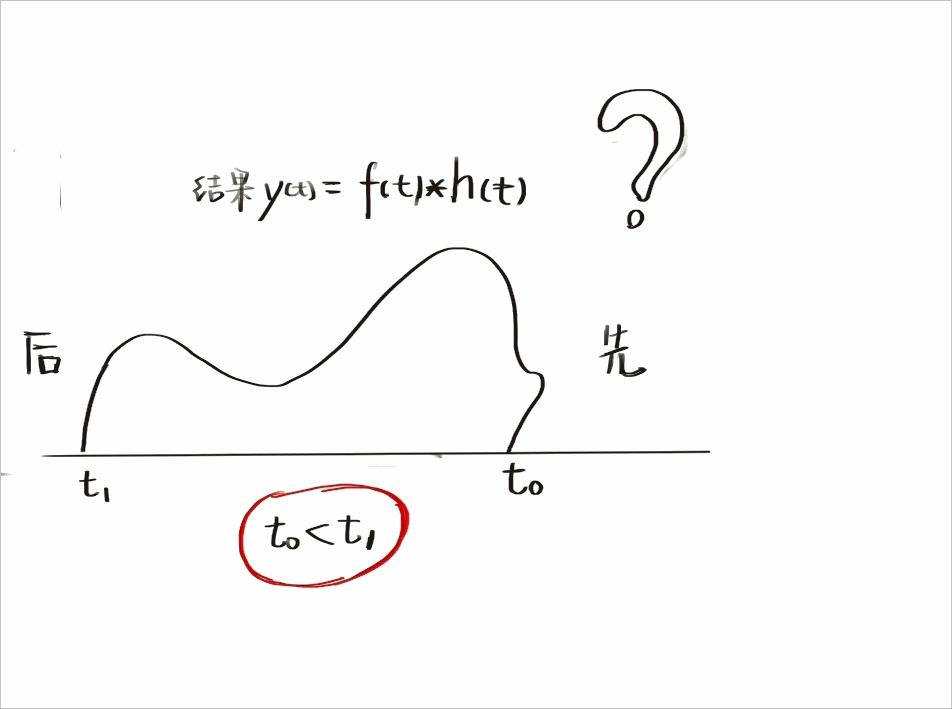
每一片冲激信号经过系统碾压之后,就形成了带有系统特殊烙印的形状,它反映了系统基本特性。
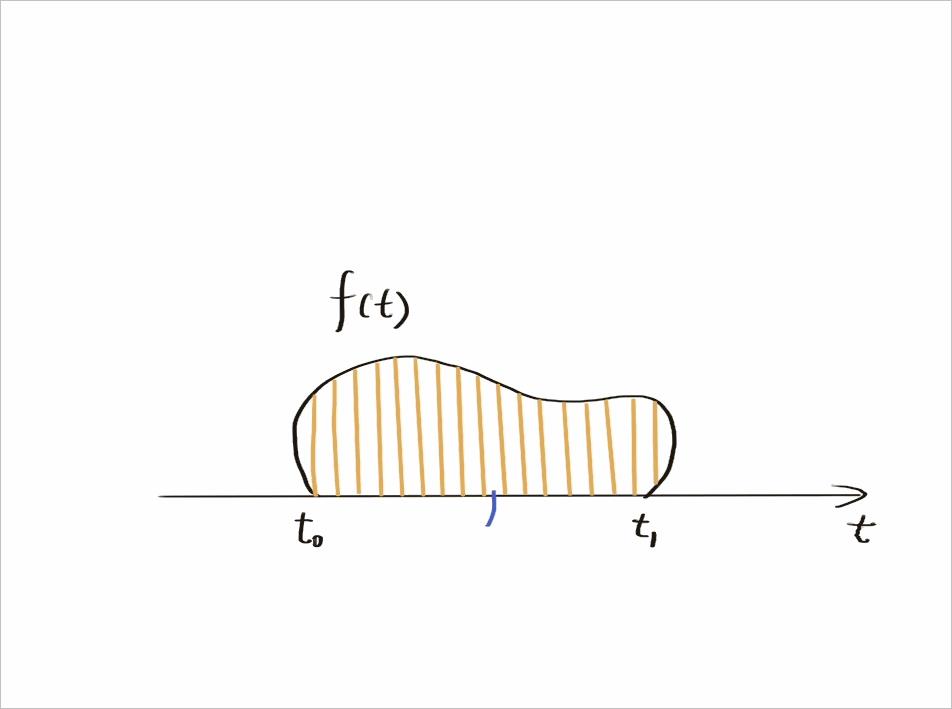
那么剩下的工作,就是将那坨面片一个一个按顺序送进系统这台面条机内,看着这些输出成型之物,在按照纵向叠加,就形成了原来信号作用在系统上的“零状态输出”。

最后一段中的一个细节,将卷积运算中“卷”字解释清楚了,也就为什么积分号中
h
(
t
)
h\\left( t \\right)
h(t)要反褶。你们仔细看在最后叠加的时候,那些面片的输出排解的时候,是从前往后排列开,形成往后移动的效果。这个动态过程表现了“卷积”的神态。这曾经让很多最初接触卷积运算的人感到不解,被这动画传神的表现了。
好的吧,下面让我们完整的看一下带有配音的完整动画片片吧。
卷积:可以这么讲的。
以上是关于一位被信号与系统耽误了的漫画家的主要内容,如果未能解决你的问题,请参考以下文章