数据结构期末不挂科笔记

Posted 2021-07-05 woodwhale

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构期末不挂科笔记相关的知识，希望对你有一定的参考价值。

【数据结构】期末不挂科笔记

大纲去复习

简答题

1、哈夫曼树的构造、计算wpl

哈夫曼树的处理其实很简单，将所有的权值节点放入最小优先队列中，每次取队头的两个数出来，组成一棵树，这颗树就三个节点，头节点是两个子节点的权值和。然后将新形成的头节点放入原先的最小优先队列中，循环上述过程就成为了一颗哈夫曼树。

给出具体例子：

给出8个带有权值的节点
将这些节点放入最小优先队列中，选择最小的两个权值节点——2、3出队，同时算出这两个节点的和为5

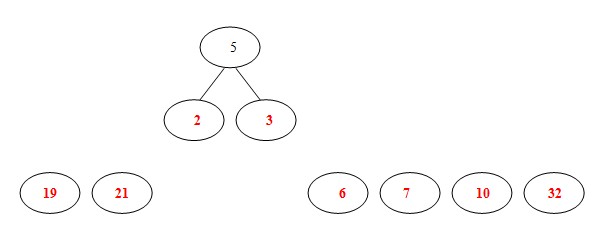
将刚刚得到的5权值节点放入初始的最小优先队列中，并再次pop出两个最小的权值节点，这次选择5、6，计算出和为11

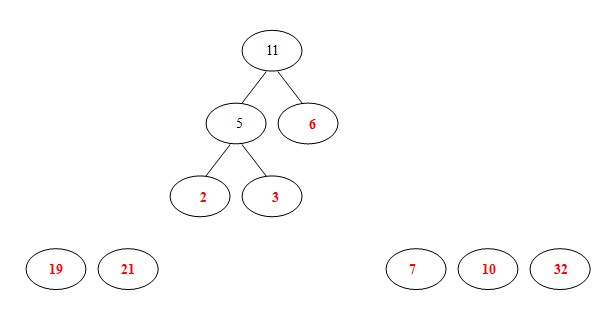
重复上述操作，我们发现现在的最小优先队列的值为[7, 10, 11, 19, 21, 32]，而我们这次出队的两个节点7、10都不是已经构造号的二叉树里面的节点，所以需要另外开一颗二叉树，这个树就是 17、7、10（头、左、右）

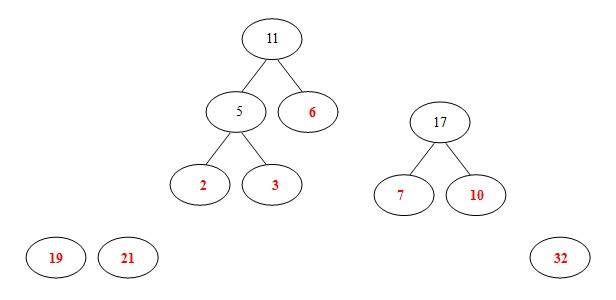
现在的队列中[11, 17, 19 ,21, 32]，选取11、17，计算出和为28，构建28、11、17的树

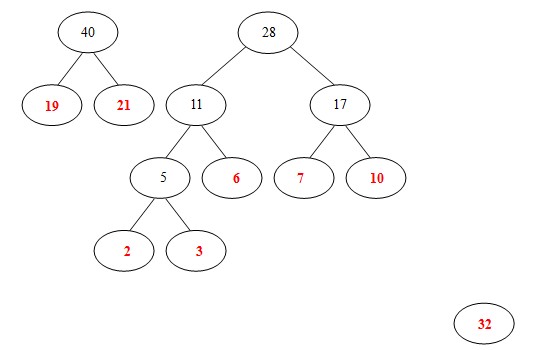
现在的队列是[28, 32, 40]，选出28、32，计算出和为60，构建60、28、32
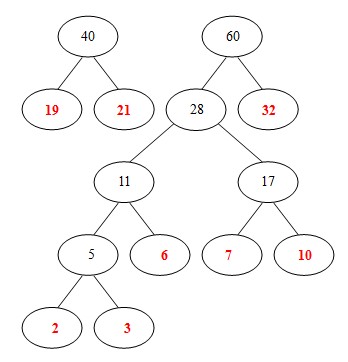
现在队列是[40, 60]，就只剩两个了，和为100，构建100、40、60

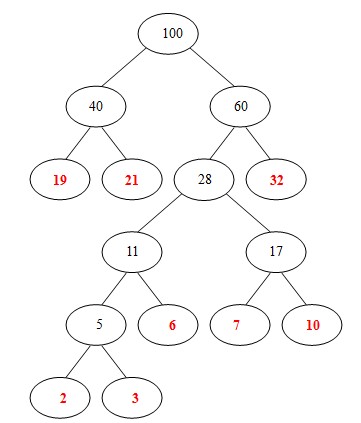
到此哈夫曼树构建完毕。

至于计算wpl，其实也很简单

我们画出来的哈夫曼树是可以看到层数的，wpl的值就是

A1最开始的权值数据 × A1爬到顶的步数 + A2最开始的权值数据 × A2爬到顶的步数 … + An最开始的权值数据 × An爬到顶的步数

什么意思呢，我们拿上面的哈夫曼树举例子

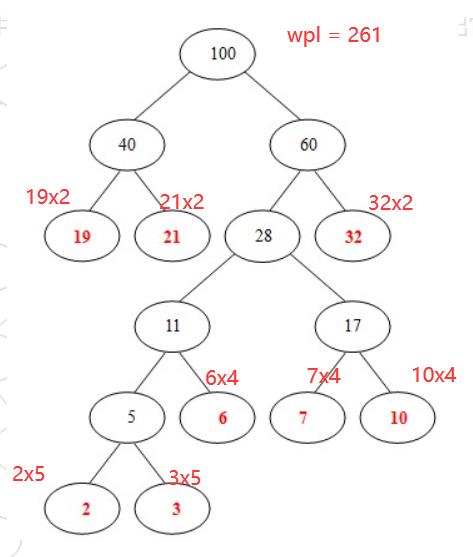
红点标注的就是最初始的数据，乘的就是爬到顶部的步数，例如2这个权值节点，爬到100这个节点就要5步，所以乘5

2、哈希表、计算平均查找长度asl

哈希表也叫散列表

哈希表的构建方法书上右6种，重点就是直接定址

处理哈希冲突的方法也有几种：开放地址法（求余）

其中，对增量d右三种取法

线性探测再散列
平方探测再散列
随机探测再散列

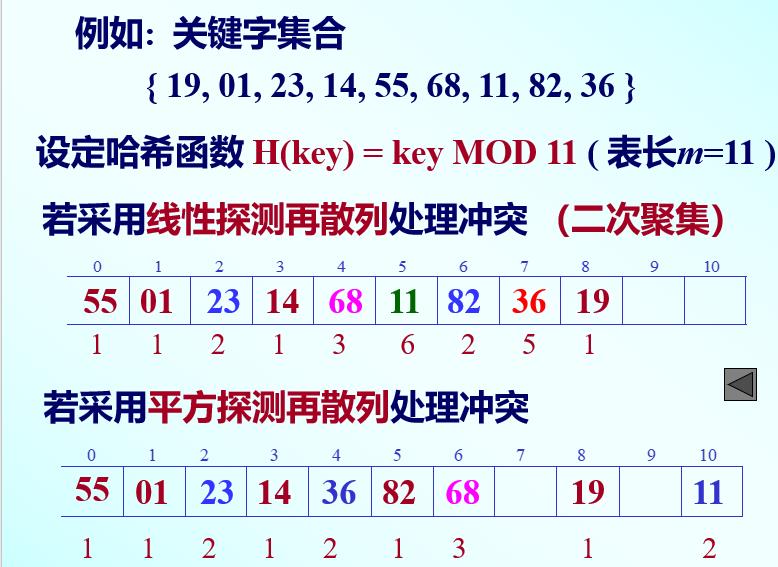
线性探测就是每一次＋1

平方探测就是每次＋1平方、负的1平方、2平方、负的2平方、3平方、负的3平方…以此类推

链地址法：

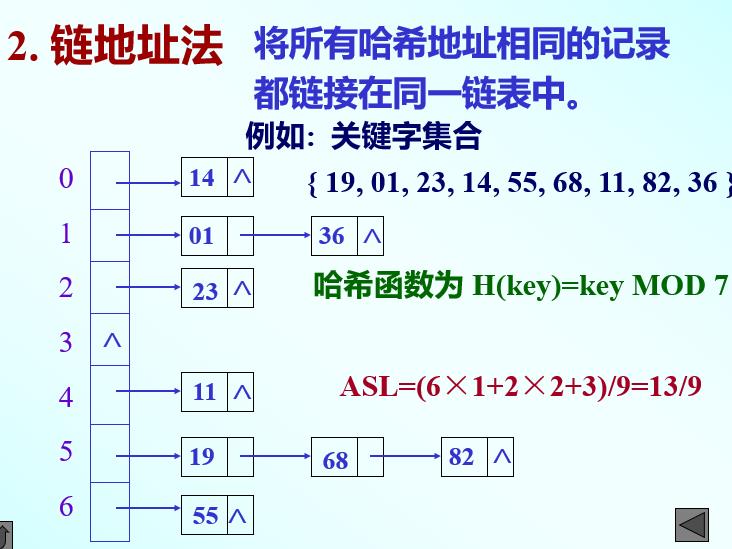
asl就是

每层冲突的次数之和 / 冲突总次数

3、最短路径

最短路径就是Dij算法和佛洛依德算法，既然老师说佛洛依德不考，那就是Dij算法了，详情见我的另一篇博客

4、堆排序、建堆

堆排序我也写过博客

5、avl树，bst树（两者出现一个）

AVL 树是一种平衡二叉树。平衡二叉树递归定义如下：

左右子树的高度差小于等于 1。
其每一个子树均为平衡二叉树。

基于这一句话，我们就可以进行判断其一棵树是否为平衡二叉了。

bst树就是二叉搜索树，avl树不需要平衡的需求，只需要满足排序大小为（左 < 头 < 右）即可

avl和bst树是动态查找，相比静态查找，有插入和删除功能。

avl的左旋右旋操作这里就得自己看了，我这边一时半会说不清。

编程题

1、二叉树的叶子节点个数（递归）

这题就比期中考试多了个判断条件——叶子节点

int LeafNodeNum(StructNode Node) {
    if (Node == NULL) {
        return 0;
    }
    if (Node->left == NULL && Node->right == NULL) {
        return 1;
    }
    return LeafNodeNum(Node->left) + LeafNodeNum(Node->right);
}

2、折半查找（二分查找）

这题目也不知道具体形式是啥

折半查找的前提是有序

关键判断条件

if (mid < search) {
    left = mid + 1;
}
else if (mid > search) {
    right = mid - 1;
}else {
    return mid;
}

填空、选择

1、排序的时间复杂度（最好、最坏、平均）

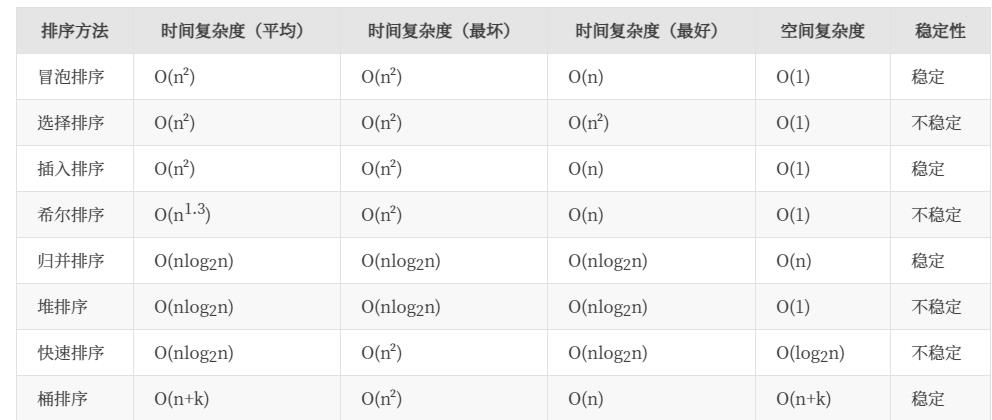
选择排序最好的情况也需要O（n^2）
快速排序最坏情况就是倒序情况，退化成冒泡排序，时间复杂度为O（n^2）
快速排序的空间复杂度为O（logn），这是辅助栈的空间
归并排序的空间复杂度为O（n），这是辅助数组的空间

2、基数排序

基数排序的特点：从个位开始，次位优先

3、队列、栈，判断空与满

队头：front

队尾：rear

队列最大大小：M（maxsize）

循环队列空：（rear + 1） % M != front

循环队列满：（rear + 1） % M = front

循环队列长度：（front - rear + M） % M

栈顶：top

栈底：base

栈空：top = base

栈满：top - base >= stacksize

4、二叉树的性质

二叉树的三种遍历得会吧
二叉树有以下几个性质：TODO(上标和下标)
性质1：二叉树第i层上的结点数目最多为 2^{i-1} (i≥1)。
性质2：深度为k的二叉树至多有(2^{k})-1个结点(k≥1)。
性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4：在任意一棵二叉树中，若叶子结点的个数为n0，度为2的结点数为n2，则n0=n2+1