LeetCode 815. 公交路线 / 909. 蛇梯棋（还是bfs）/ 168. Excel表列名称 / 171. Excel表列序号

Posted 2021-07-05 Zephyr丶J

815. 公交路线

2021.6.28 每日一题

题目描述

给你一个数组 routes ，表示一系列公交线路，其中每个 routes[i] 表示一条公交线路，第 i 辆公交车将会在上面循环行驶。

例如，路线 routes[0] = [1, 5, 7] 表示第 0 辆公交车会一直按序列 1 -> 5 -> 7 -> 1 -> 5 -> 7 -> 1 -> ... 这样的车站路线行驶。
现在从 source 车站出发（初始时不在公交车上），要前往 target 车站。 期间仅可乘坐公交车。

求出 最少乘坐的公交车数量 。如果不可能到达终点车站，返回 -1 。

 

示例 1：

输入：routes = [[1,2,7],[3,6,7]], source = 1, target = 6
输出：2
解释：最优策略是先乘坐第一辆公交车到达车站 7 , 然后换乘第二辆公交车到车站 6 。 
示例 2：

输入：routes = [[7,12],[4,5,15],[6],[15,19],[9,12,13]], source = 15, target = 12
输出：-1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/bus-routes
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

还是BFS，一遍过
与之前有所不同的是，这里开始加入队列的可能有多个公交车，因为可能有多个公交车经过source站点
需要预处理，将每个站点上经过的公交车存储在一个哈希表中，方便后面的查找

class Solution {
    public int numBusesToDestination(int[][] routes, int source, int target) {
        //感觉就还是和前两天的一样，还是广度优先搜索吧
        //从第一个点开始遍历所有能到达的结点，然后直到到达target
        if(target == source)
            return 0;
        int l = routes.length;
        //先将每个站点上经过的公交车号存储在哈希表中，方便查找
        Map<Integer, List<Integer>> map = new HashMap<>();

        for(int i = 0; i < l; i++){
            for(int pos : routes[i]){
                if(map.containsKey(pos)){
                    map.get(pos).add(i);
                }else{
                    List<Integer> list = new ArrayList<>();
                    list.add(i);
                    map.put(pos, list);
                }
            }
        }
        //存储走过的公交车吧
        Set<Integer> set = new HashSet<>();

        Queue<Integer> queue = new LinkedList<>();
        //第一个站点，可以乘坐的公交车有多个
        List<Integer> first = map.get(source);
        for(int num : first){
            queue.add(num);
            set.add(num);
        }
        int step = 0;
        while(!queue.isEmpty()){
            step++;
            int size = queue.size();
            while(size-- > 0){
                //第几辆公交车
                int index = queue.poll();
                //能到达的站点
                int[] pos = routes[index];
                for(int p : pos){
                    //如果坐这辆车能到达target，就返回step
                    if(p == target)
                        return step;
                    //否则得到这个站点能坐的公交车
                    List<Integer> temp = map.get(p);
                    for(int num : temp){
                        if(set.contains(num))
                            continue;
                        set.add(num);
                        queue.add(num);
                    }
                }
            }
        }
        return -1;
        
    }
}

本来觉得官解的方法麻烦了，就看别的了，但是转念一想，好像不是这样，所以也学习了一下

class Solution {
    //看一下官解的这个思路
    //建图，如果两个公交车之间能到达，就为true，并且同样存储经过每个站点的公交车
    //然后用一个dis存储出发点到其他每个车站所需要乘坐公交车的数目
    //然后进行广度优先搜索更新这个dis数组
    //最后在目标为target的站点中找需要乘坐公交车最少的
    public int numBusesToDestination(int[][] routes, int source, int target) {
        if (source == target) {
            return 0;
        }

        int n = routes.length;
        boolean[][] edge = new boolean[n][n];
        Map<Integer, List<Integer>> rec = new HashMap<Integer, List<Integer>>();
        for (int i = 0; i < n; i++) {
            for (int site : routes[i]) {
                List<Integer> list = rec.getOrDefault(site, new ArrayList<Integer>());
                //两个站点可以连通，即为true
                for (int j : list) {
                    edge[i][j] = edge[j][i] = true;
                }
                list.add(i);
                rec.put(site, list);
            }
        }
        //出发点到其他公交车经过的公交车数目
        int[] dis = new int[n];
        Arrays.fill(dis, -1);
        Queue<Integer> que = new LinkedList<Integer>();
        for (int bus : rec.getOrDefault(source, new ArrayList<Integer>())) {
            dis[bus] = 1;
            que.offer(bus);
        }

        while (!que.isEmpty()) {
            int x = que.poll();
            for (int y = 0; y < n; y++) {
                //如果两个公交车能换乘，并且此时到达y车的距离还没有被更新过，那么就进行更新
                if (edge[x][y] && dis[y] == -1) {
                    dis[y] = dis[x] + 1;
                    que.offer(y);
                }
            }
        }
        //遍历目标站点对应的公交车
        int ret = Integer.MAX_VALUE;
        for (int bus : rec.getOrDefault(target, new ArrayList<Integer>())) {
            if (dis[bus] != -1) {
                ret = Math.min(ret, dis[bus]);
            }
        }
        return ret == Integer.MAX_VALUE ? -1 : ret;
    }
}

909. 蛇梯棋

2021.6.27 每日一题

题目描述

N x N 的棋盘 board 上，按从 1 到 N*N 的数字给方格编号，编号 从左下角开始，每一行交替方向。

例如，一块 6 x 6 大小的棋盘，编号如下：

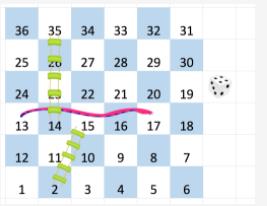
r 行 c 列的棋盘，按前述方法编号，棋盘格中可能存在 “蛇” 或 “梯子”；如果 board[r][c] != -1，那个蛇或梯子的目的地将会是 board[r][c]。

玩家从棋盘上的方格 1 （总是在最后一行、第一列）开始出发。

每一回合，玩家需要从当前方格 x 开始出发，按下述要求前进：

选定目标方格：选择从编号 x+1，x+2，x+3，x+4，x+5，或者 x+6 的方格中选出一个目标方格 s ，目标方格的编号 <= N*N。
该选择模拟了掷骰子的情景，无论棋盘大小如何，你的目的地范围也只能处于区间 [x+1, x+6] 之间。
传送玩家：如果目标方格 S 处存在蛇或梯子，那么玩家会传送到蛇或梯子的目的地。否则，玩家传送到目标方格 S。 
注意，玩家在每回合的前进过程中最多只能爬过蛇或梯子一次：就算目的地是另一条蛇或梯子的起点，你也不会继续移动。

返回达到方格 N*N 所需的最少移动次数，如果不可能，则返回 -1。


示例：

输入：[
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
输出：4
解释：
首先，从方格 1 [第 5 行，第 0 列] 开始。
你决定移动到方格 2，并必须爬过梯子移动到到方格 15。
然后你决定移动到方格 17 [第 3 行，第 5 列]，必须爬过蛇到方格 13。
然后你决定移动到方格 14，且必须通过梯子移动到方格 35。
然后你决定移动到方格 36, 游戏结束。
可以证明你需要至少 4 次移动才能到达第 N*N 个方格，所以答案是 4。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/snakes-and-ladders
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这个题，首先得认真读题。而且我觉得题还不一定对，做起来好难受
刚开始我还是常规bfs思路写的，每次移动一步，然后用一个used数组存储到达过的点，然后过了202个例子，解答错误了，代码如下

class Solution {
    int[][] board;
    int n;
    public int snakesAndLadders(int[][] board) {
        //还是广度优先搜索，想了一下，感觉也不需要考虑矩阵啊，到点跳就行了,o，需要在矩阵中找标号
        this.board = board;
        this.n = board.length;
        int target = n * n;

        Queue<Integer> queue = new LinkedList<>();
        boolean[] used = new boolean[n * n + 1];
        used[1] = true;
        queue.add(1);
        
        int step = 0;
        while(!queue.isEmpty()){
            step++;
            int size = queue.size();
            while(size-- > 0){
                //当前位置编号
                int temp = queue.poll();
                for(int i = 1; i <= 6; i++){
                    if(temp + i == target)
                        return step;
                    if(used[temp + i])
                        continue;
                    int index = temp + i;
                    used[index] = true;
                    //得到当前位置在board中对应的下标
                    int pos = getPos(index);
                    if(pos != -1){
                        if(pos == target)
                            return step;
                        if(!used[pos]){
                            used[pos] = true;
                            queue.add(pos);
                        }
                    }else{
                        queue.add(index);
                    }
                }
            }
        }
        return -1;
    }

    public int getPos(int index){
        //偶数行正向，奇数行反向
        int col = (index - 1) / n;
        int row = (index - 1) % n;
        return col % 2 == 0 ? board[n - 1 - col][row] : board[n - 1 - col][n - row - 1]; 
    }
}

然后我去研究了一下这个测试用例：
[[-1,-1,-1,46,47,-1,-1,-1],[51,-1,-1,63,-1,31,21,-1],[-1,-1,26,-1,-1,38,-1,-1],[-1,-1,11,-1,14,23,56,57],[11,-1,-1,-1,49,36,-1,48],[-1,-1,-1,33,56,-1,57,21],[-1,-1,-1,-1,-1,-1,2,-1],[-1,-1,-1,8,3,-1,6,56]]
发现这个例子中梯子到达的点位置还有梯子，然后我还以为是能连环跳的，就把代码改了一下，让可以进行连环的跳跃，结果又失败了，这个例子给出的答案是4，连环跳跃给出的答案是3，然后我看了一下题目要求，发现每次只能跳一次，意思是由多个梯子连接也只能跳一次
然后我又改回原来的代码，因为原来的代码就是跳一次，但是有个问题不太明白，就是如果跳一次，而跳过去的位置有梯子，那么下一次是继续爬梯子呢，还是掷骰子了，如果爬上去梯子是否还能掷骰子。然后我就凌乱了，不知道咋写了，就去看答案了

官解给的答案我看了一下，还是相当于每次只能跳一个梯子，但是如果两个梯子相连，第二次是不会去走梯子的，而是去掷骰子。。。然后我就觉得我的代码应该没问题啊，为什么会错呢
然后仔细和官解对照了一下，发现区别在于，我的逻辑中，如果当前位置已经为true，那么我认为这个位置的情况已经遍历过了，就直接continue；而官解中对标记为true的位置同样进行遍历。
想想为什么，对于我出现错误的这个用例，如果按照我的逻辑，4的位置有梯子到达8位置，然后标记为true了，但是这个位置其实是还有梯子可以跳跃的，那么当再遍历到这个位置的时候，我的代码将不会发生跳跃。而按官解中的逻辑，这个位置同样会发生跳跃，到达56的位置。

这道题就这样吧，看看就完事了，感觉出的乱七八糟的，最起码描述没描述清楚

class Solution {
    int[][] board;
    int n;
    public int snakesAndLadders(int[][] board) {
        //还是广度优先搜索，想了一下，感觉也不需要考虑矩阵啊，到点跳就行了,o，需要在矩阵中找标号
        this.board = board;
        this.n = board.length;
        int target = n * n;

        Queue<Integer> queue = new LinkedList<>();
        boolean[] used = new boolean[n * n + 1];
        used[1] = true;
        queue.add(1);
        
        int step = 0;
        while(!queue.isEmpty()){
            step++;
            int size = queue.size();
            while(size-- > 0){
                //当前位置编号
                int temp = queue.poll();
                for(int i = 1; i <= 6; i++){
                    int index = temp + i;
                    if(index == target)
                        return step; 
                    //得到当前位置在board中对应的下标
                    int pos = getPos(index);
                    if(pos != -1){
                        used[index] = true;
                        //如果数组中这个位置不为-1，那么继续找下一个位置
                        if(pos == target)
                            return step;
                        if(!used[pos]){
                            used[pos] = true;
                            queue.add(pos);
                        }
                    }else{
                        if(!used[index]){
                            used[index] = true;
                            queue.add(index);
                        }
                    }
                }
            }
        }
        return -1;
    }

    public int getPos(int index){
        //偶数行正向，奇数行反向
        int row = (index - 1) / n;
        int col = (index - 1) % n;
        return row % 2 == 0 ? board[n - 1 - row][col] : board[n - 1 - row][n - col - 1]; 
    }
}

168. Excel表列名称

2021.6.29每日一题

题目描述

给定一个正整数，返回它在 Excel 表中相对应的列名称。

例如，

    1 -> A
    2 -> B
    3 -> C
    ...
    26 -> Z
    27 -> AA
    28 -> AB 
    ...
示例 1:

输入: 1
输出: "A"
示例 2:

输入: 28
输出: "AB"
示例 3:

输入: 701
输出: "ZY"

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/excel-sheet-column-title
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

相当于一个26进制的数

class Solution {
    public String convertToTitle(int columnNumber) {
        StringBuffer sb = new StringBuffer();
        while(columnNumber != 0){
            int remainder = (columnNumber - 1) % 26;
            columnNumber = (columnNumber - 1) / 26;
            sb.append((char)(remainder + 'A'));
        }
        return sb.reverse().toString();
    }
}

171. Excel表列序号

题目描述

给定一个Excel表格中的列名称，返回其相应的列序号。

例如，

    A -> 1
    B -> 2
    C -> 3
    ...
    Z -> 26
    AA -> 27
    AB -> 28 
    ...
示例 1:

输入: "A"
输出: 1
示例 2:

输入: "AB"
输出: 28
示例 3:

输入: "ZY"
输出: 701

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/excel-sheet-column-number
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

class Solution {
    public int titleToNumber(String columnTitle) {
        int l = columnTitle.length();
        int res = 0;
        for(int i = 0; i < l; i++){
            res = res * 26 + columnTitle.charAt(i) + 1 - 'A';
        }
        return res;
    }
}