基于Eigen库的线性方程组/矩阵方程求解(方法汇总)
Posted 借我十斤肉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于Eigen库的线性方程组/矩阵方程求解(方法汇总)相关的知识,希望对你有一定的参考价值。
文章目录
前言
Eigen 是一个基于C++模板的线性代数库,提供了很多求解矩阵方程的方式,如比如LU分解、QR分解、SVD分解等。
本文以实用性为主,重点讨论几种求解矩阵方程的方法,以及不同方法的优缺点。对于每种方法的原理不做过多介绍。
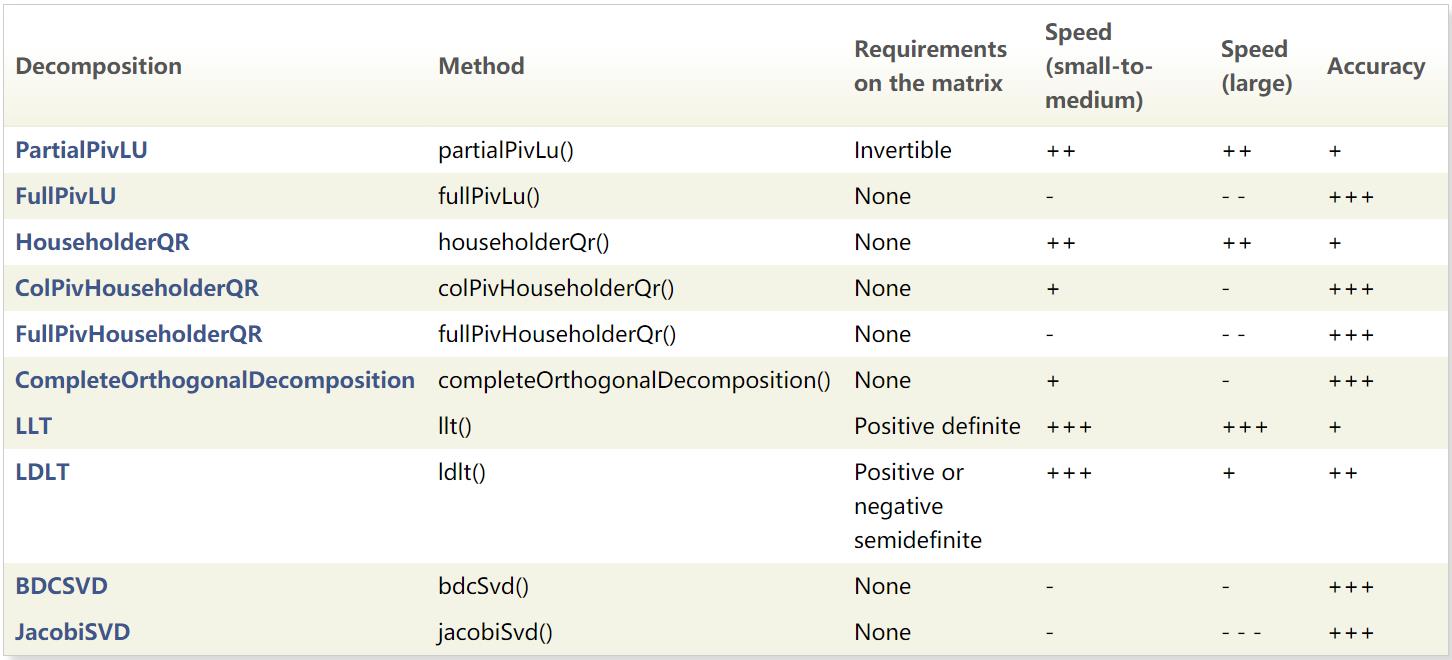
下面给出不同分解方式的对比图,主要是计算速度和精度的对比,同时不同的分解方式对系数矩阵的形式也有不同的要求。
1 线性方程组(矩阵方程)
线性方程组是各个方程关于未知量均为一次的方程组,可以采用矩阵方程的形式表示。比如已知一个线性方程组
{
a
1
x
1
+
b
1
x
2
+
c
1
x
3
=
d
1
a
2
x
1
+
b
2
x
2
+
c
2
x
3
=
d
2
a
3
x
1
+
b
3
x
2
+
c
3
x
3
=
d
3
\\begin{cases} a_1x_1+b_1x_2+c_1x_3=d_1\\\\ a_2x_1+b_2x_2+c_2x_3=d_2\\\\ a_3x_1+b_3x_2+c_3x_3=d_3\\\\ \\end{cases}
⎩⎪⎨⎪⎧a1x1+b1x2+c1x3=d1a2x1+b2x2+c2x3=d2a3x1+b3x2+c3x3=d3
写成矩阵形式
A
x
=
b
Ax=b
Ax=b
其中,
A = [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] A=\\begin{bmatrix}a_1&b_1&c_1 \\\\a_2&b_2&c_2\\\\a_3&b_3&c_3\\\\\\end{bmatrix} A=⎣⎡a1a2a3b1b2b3c1c2c3⎦⎤, x = [ x 1 x 2 x 3 ] x=\\begin{bmatrix}x_1\\\\x_2\\\\x_3\\\\\\end{bmatrix} x=⎣⎡x1x2x3⎦⎤, d = [ d 1 d 2 d 3 ] d=\\begin{bmatrix}d_1\\\\d_2\\\\d_3\\\\\\end{bmatrix} d=⎣⎡d1d2d3⎦⎤
以线性方程组
{
x
1
+
2
x
2
+
3
x
3
=
3
4
x
1
+
5
x
2
+
6
x
3
=
3
7
x
1
+
8
x
2
+
10
x
3
=
4
\\begin{cases} x_1+2x_2+3x_3=3\\\\ 4x_1+5x_2+6x_3=3\\\\ 7x_1+8x_2+10x_3=4\\\\ \\end{cases}
⎩⎪⎨⎪⎧x1+2x2+3x3=34x1+5x2+6x3=37x1+8x2+10x3=4
为例,进行求解。写成矩阵形式为
[
1
2
3
4
5
6
7
8
10
]
[
x
1
x
2
x
3
]
=
[
3
3
4
]
\\begin{bmatrix}1&2&3 \\\\4&5&6\\\\7&8&10\\\\\\end{bmatrix}\\begin{bmatrix}x_1\\\\x_2\\\\x_3\\\\\\end{bmatrix}=\\begin{bmatrix}3\\\\3\\\\4\\\\\\end{bmatrix}
⎣⎡1472583610⎦⎤⎣⎡x1x2以上是关于基于Eigen库的线性方程组/矩阵方程求解(方法汇总)的主要内容,如果未能解决你的问题,请参考以下文章