快速掌握二叉树的7种遍历方式哦！！！

Posted 2021-07-04 SSimeng

二叉树的7种遍历

• 1. 树节点结构的定义
• 2. 树的创建
• 3. 树的深度优先遍历
• • 3.1 树的前序遍历【根左右】（递归和非递归）
  • 3.2 树的中序遍历【左根右】（递归和非递归）
  • 3.3 树的后序遍历【左右根】（递归和非递归）
• 4. 树的广度优先遍历（层序遍历）

1. 树节点结构的定义

树是由一个个节点组成的结构，有个特殊的结点是根节点，而每个结点由自己的左孩子结点和右孩子结点组成。

树的结构图：

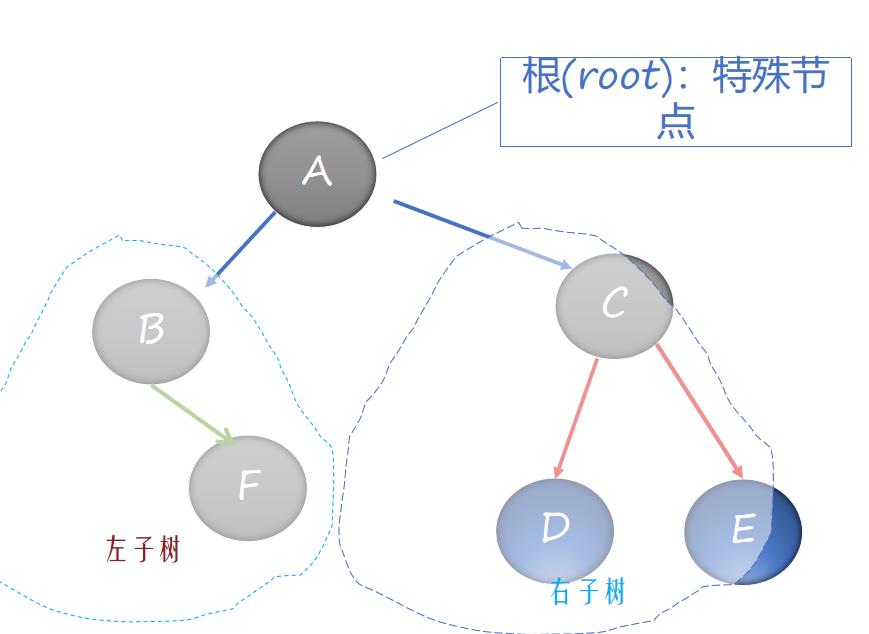
接下来是对树中节点的定义：

/**
 * 树节点结构的定义
 * @author Simeng
 *
 */
public class TreeNode {
	private int data;//数据域
	private TreeNode left;//左子结点
	private TreeNode right;//右节点
	public TreeNode(int data, TreeNode left, TreeNode right) {
		this.data = data;
		this.left = left;
		this.right = right;
	}
	@Override
	public String toString() {
		return "TreeNode [data=" + data + ", left=" + left + ", right=" + right + "]";
	}
	

}

2. 树的创建

有了节点，我们就要拼凑，定义方法去构建一棵二叉树。
（1）树的定义：

/**
 * 定义树的结构
 * @author 司蒙
 *
 */
public class Tree {
	private TreeNode root;//树的根节点
	private int size;//树的节点的个数
	
	public TreeNode getRoot() {
		return root;
	}
}

（2）树的创建

/**
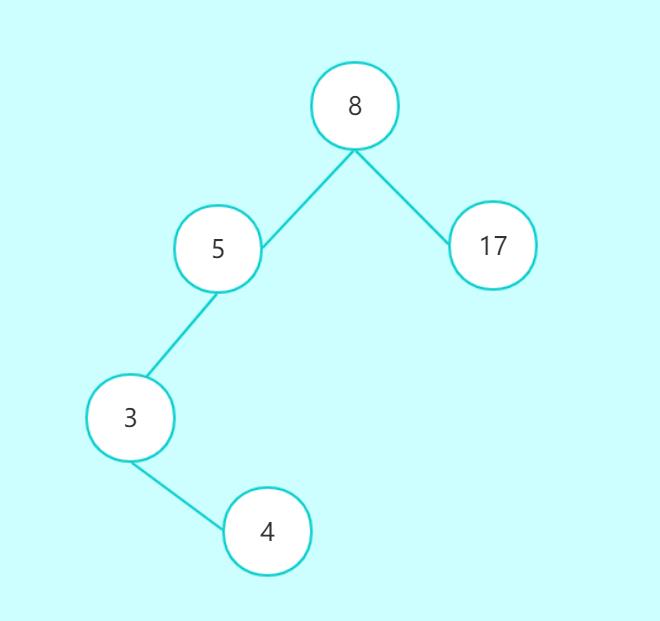
	 * 构建一棵二叉树,返回树的根节点
	 */
	public void buildTree(int data) {
		if (root == null) {
			 root = new TreeNode(data);// 当为空树时，直接将data封装成一个node对象，赋值给root，作为树的根节点
		}else {
			// 不为空
			TreeNode currentNode = root;
			while(true) {
				if (data < currentNode.data) {// 在左子树这边
					if (currentNode.left == null) {
						currentNode.left = new TreeNode(data);// 如果子节点为空，直接将新的节点挂到上面去即可						
						return;
					} else {
						currentNode = currentNode.left;
					}
				}else {//data>currentNode.data,在右子树这边添加
					if (currentNode.right == null) {
						currentNode.right = new TreeNode(data);// 如果子节点为空，直接将新的节点挂到上面去即可
						return;
					} else {
						currentNode = currentNode.right;
					}
					
				}
			}
		}
		this.size++;//添加后，节点个数要增加
	}

public class TestTree {
	public static void main(String[] args) {
		Tree t=new Tree();//构建树
		t.buildTree(8);
		t.buildTree(5);
		t.buildTree(3);
		t.buildTree(4);
		t.buildTree(17);
	}
}

3. 树的深度优先遍历

3.1 树的前序遍历【根左右】（递归和非递归）

①递归做法

/**
	 * 二叉树的前序遍历(递归)
	 * 
	 * @param root
	 */
	public void preOrder1(TreeNode root) {
		if (root == null)
			return;
		System.out.print(root.data + " ");
		preOrder1(root.left);
		preOrder1(root.right);

	}

②迭代做法

/**
	 * 二叉树的前序遍历（迭代）
	 * @param root
	 */
	public void preOrder2(TreeNode root) {
		Stack<TreeNode> stack=new Stack<TreeNode>();
		TreeNode currNode=root;
		if(currNode!=null) {
			stack.push(currNode);//将根节点入栈
			while(!stack.isEmpty()) {
				currNode=stack.pop();
				System.out.println(currNode.data+" ");
				if(currNode.right!=null) {
					stack.push(currNode.right);//由于栈结构，先压右节点
				}
				if(currNode.left!=null) {
					stack.push(currNode.left);
				}
			}
		}
	}

前序遍历测试

public class TestTree {
	public static void main(String[] args) {
		Tree t=new Tree();//构建树
		t.buildTree(8);
		t.buildTree(5);
		t.buildTree(3);
		t.buildTree(4);
		t.buildTree(17);
		System.out.print("树的前序遍历（递归）为：[");
		t.preOrder1(t.getRoot());
		System.out.println("]");
		
		System.out.print("树的前序遍历（迭代）为：[");
		t.preOrder2(t.getRoot());
		System.out.println("]");
	}
}

3.2 树的中序遍历【左根右】（递归和非递归）

①递归

/**
	 * 二叉树的中序遍历(递归)
	 * 
	 * @param root
	 */
	public void inOrder1(TreeNode root) {
		if (root == null)
			return;
		inOrder1(root.left);
		System.out.print(root.data + " ");
		inOrder2(root.right);
	}
	

②迭代

/**
	 * 二叉树的中序遍历（迭代）
	 * 
	 * @param root
	 */
	public void inOrder2(TreeNode root) {
		Stack<TreeNode> stack = new Stack<TreeNode>();
		TreeNode currNode=root;
		while(currNode !=null || !stack.isEmpty()) {
			
			while(currNode!=null) {
				stack.push(currNode);
				currNode=currNode.left;
			}
			if(!stack.isEmpty()) {
				currNode=stack.pop();//弹出左结点
				System.out.print(currNode.data+" ");
				currNode=currNode.right;
			}
		}

	}

中序遍历测试：

        System.out.print("树的中序遍历（递归）为：[");
		t.inOrder1(t.getRoot());
		System.out.println("]");
		
		System.out.print("树的中序遍历（递归）为：[");
		t.inOrder2(t.getRoot());
		System.out.println("]");

中序测试结果：

3.3 树的后序遍历【左右根】（递归和非递归）

①递归

/**
	 * 二叉树的后序遍历(递归)
	 * 
	 * @param root
	 */
	public void afterOrder1(TreeNode root) {
		if (root == null)
			return;
		afterOrder1(root.left);
		afterOrder1(root.right);
		System.out.print(root.data + " ");
	}

②迭代

/**
	 * 二叉树的后序遍历（迭代）
	 * 
	 * @param root
	 */
	public void afterOrder2(TreeNode root) {
		Stack<TreeNode> stack = new Stack<TreeNode>();
		Stack<TreeNode> stack2=new Stack<TreeNode>();
		TreeNode curNode=root;
		while(curNode!=null || !stack.isEmpty()) {
			while(curNode!=null) {
				stack.push(curNode);
				stack2.push(curNode);
				curNode=curNode.right;
			}
			if(!stack.isEmpty()) {
				curNode=stack.pop();
				curNode=curNode.left;
			}
		}
		while(!stack2.isEmpty()) {
			curNode=stack2.pop();
			System.out.print(curNode.data+" ");
		}
	}

树的后续遍历测试结果：

4. 树的广度优先遍历（层序遍历）

/**
	 * 树的层序遍历
	 * @param root
	 */
	public void widthOrder(TreeNode root) {
		if(root==null) return;
		Queue<TreeNode> q=new LinkedList<TreeNode>();
		TreeNode curNode=root;
		q.offer(curNode);
		while(!q.isEmpty()) {
			curNode=q.poll();
			System.out.print(curNode.data+" ");
			if(curNode.left!=null) {
				q.offer(curNode.left);
			}
			if(curNode.right!=null) {
				q.offer(curNode.right);
			}
		}
	}

层序遍历测试：

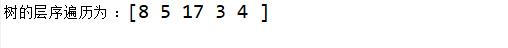
本次二叉树的遍历就到此结束了，如有问题请指正谢谢！！!