数位DP~“鉴赏“

Posted 2021-07-04 ｡✧* ꧁王者꧂✧*

数位DP，顾名思义，就是按位来进行状态转移的DP。
而且，这个按“位”，通常意义下并非十进制，根据题目的约束条件，我们要先进行进制转换，然后按位，并用上一些数学的知识进行状态转移。
数位DP通常有两个小技巧：
$1.$统计区间内满足某个条件的数的数目。$[x,y]-->f(y)-f(x-1)$
$2.$将线性问题放到树上来考虑，会直观很多。
下面有一道题，我们就借此来分析一下：

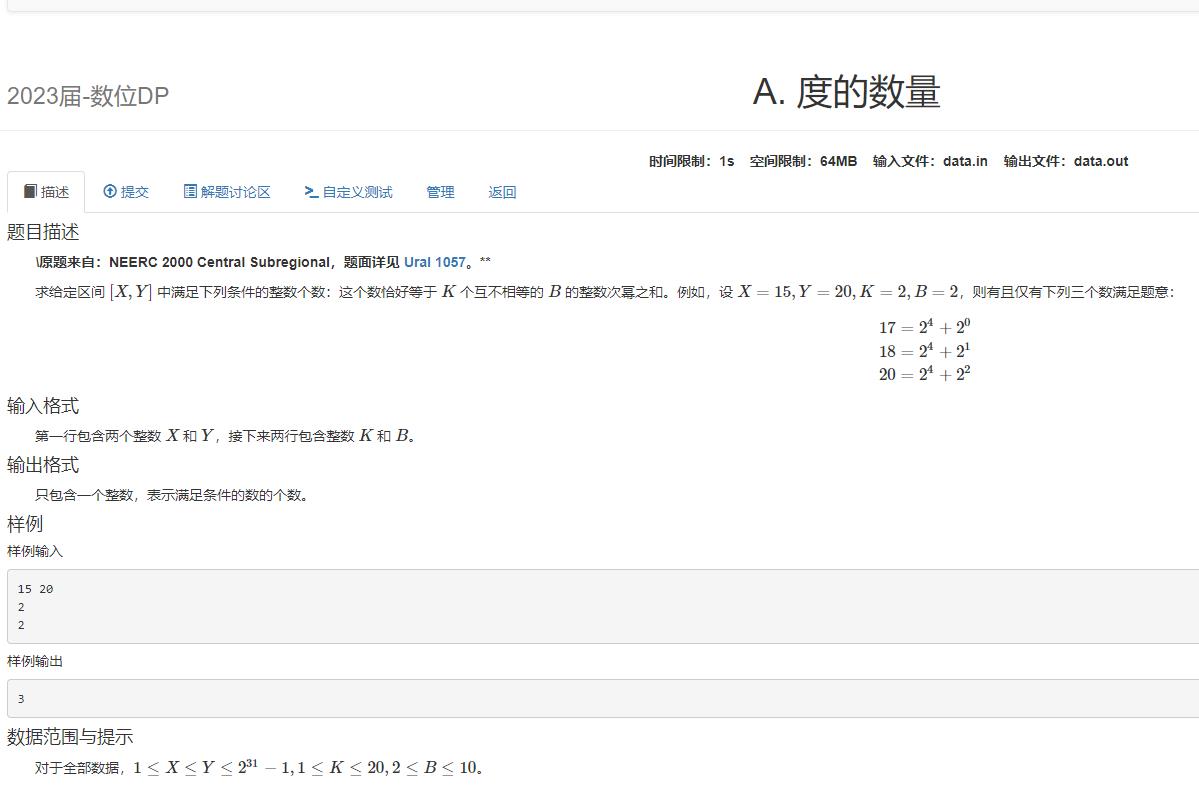
这道题就是一道典型的数位DP。
大家可以想一下，对于将某个数$x$表示成$k$的几个幂次相加的形式，我们是不是可以用进制转换，将$x$转换成$k$进制数，然后再一位一位进行分析。
如下图：
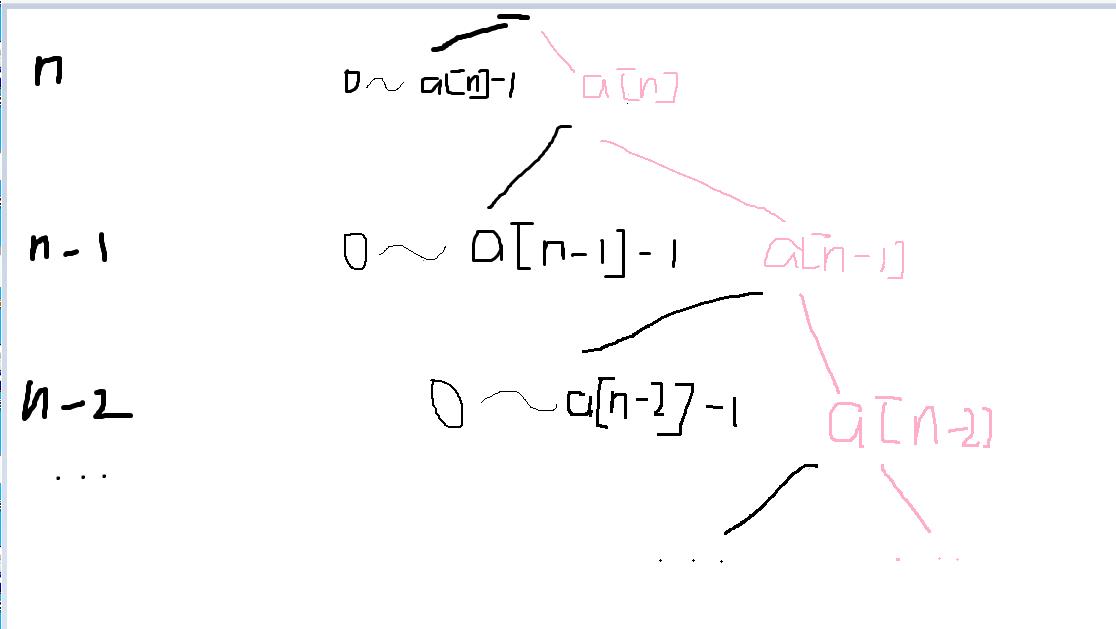将$x$进行$k$进制转换后，设有$n$位，第$i$位上数字为$a[i]$，我们从最高位开始进行状态转移。
我们先不考虑本题的“不相等的k的幂次加和”，对于第$i$位，我们将其分为两种情况：
$1.$填$0$~$a[i]-1$，那么，后面$i-1$位上的数不就可以随便填了吗，此时，又因为题目的约束每一位只能为$1$或$0$，所以，后面填$1$的方案数我们就可以用组合数来求：设此时前面的数已经填了$l$个$1$，那么，后面位置上就只能填$k-l$个$1$，若第$i$位填$1$，那答案加上$C_{i-1}^{k-l-1}$，若第$i$位填$0$，则答案加上$C_{i-1}^{k-l}$。
$2.$填$a[i]$，这样的话后面的数就不能随便填了，因为可能填了之后超过边界最大值（就比如二进制转换后是$110000$，若第$2$位填$1$，后面的位置就不能填$1$了）。

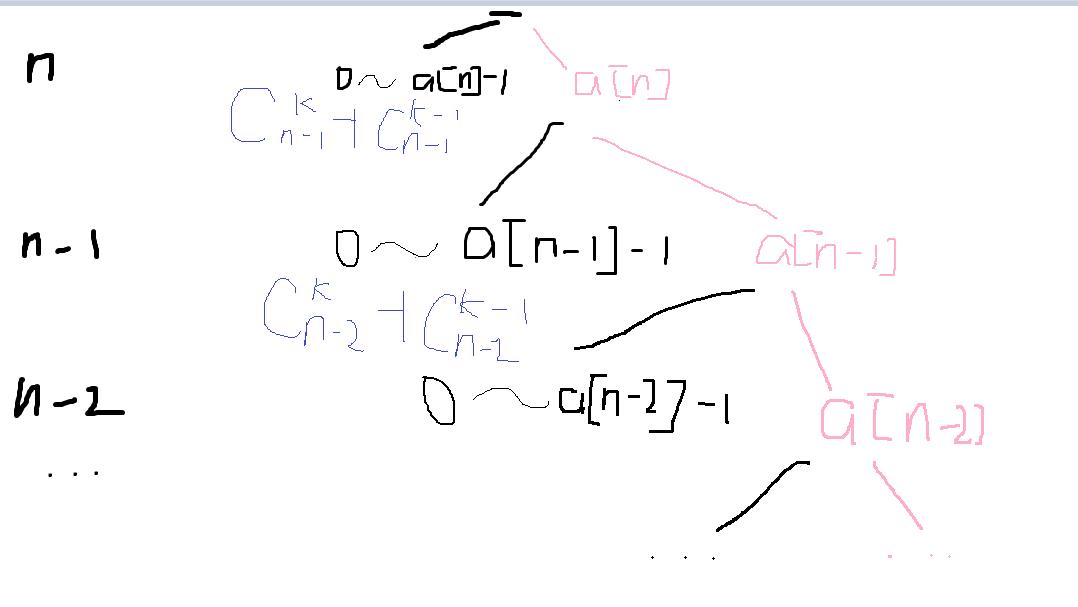
再回到这道题，根据上面我们的一波分析，又因为“不相等的k的幂次相加”，所以，当$a[i]>1$时，我们就可以直接用组合数求，然后$break$；而如果$a[i]==1$就继续向下求。
具体代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=35;
int l,r,k,A;
int f[N][N];
void init()
{
	for(int i=0;i<N;i++)
	{
		for(int j=0;j<=i;j++)
		{
			if(!j) f[i][j]=1;
			else f[i][j]=f[i-1][j-1]+f[i-1][j];
		}
	}
}
int query(int n)
{
	vector<int >num;
	while(n) num.push_back(n%A),n/=A;
	int res=0,last=0;
	for(int i=num.size()-1;i>=0;i--)
	{
		int x=num[i];
		if(x)
		{
			res+=f[i][k-last];
			if(x>1)
			{
				if(k-last-1>=0)
				res+=f[i][k-last-1];
				break;
			}
			else
			{
				last++;
				if(last>k) break;
			}
		}
		if(!i&&last==k) res++;
	}
	return res;
}
int main()
{
	cin>>l>>r>>k>>A;
	init();
	printf("%d",query(r)-query(l-1));
	return 0;
}

其实，数位DP的题目都有一个很固定的模板，但是，因为每一道题的特殊性，在处理时也会有差别。
就比如，本题用到了组合数，但还有很多的题目，其预处理大多会用到动态规划，使得对于第$1$种情况（树中向左儿子方向处理）我们可以直接求得答案。