AC自动机

Posted 2021-07-04 ｡✧* ꧁王者꧂✧*

今日份的博客来袭。
AC自动机，很疑问它为什么要叫这个名字，但这并不是重点（我管它什么名字呢~）。
曾经学kmp的时候就听教练提过一嘴，说AC自动机怎么样怎么样，今天终于见到了！（结果是我被无尽的泪水淹没了┭┮﹏┭┮）

AC自动机说难也难，因为它的本质不是特别容易理解。
但它说不难也不难，因为你只要会用就行了。

但是，相比于一知半解，还是啃透比较好吧。
学AC自动机需要两个前置技能：$KMP$和$trie$树。
但是，个人觉得这两者中，先学会$KMP$比较重要，因为AC自动机最难理解的东西其实学$KMP$时已经学过了，就是那个$next$数组。
在$KMP$中，字符串$A$的$next[i]$的含义是：$A$中以$i$结尾非前缀子串所能匹配的$A$的最大前缀。是不是挺绕的，下面我们就来画一波图：

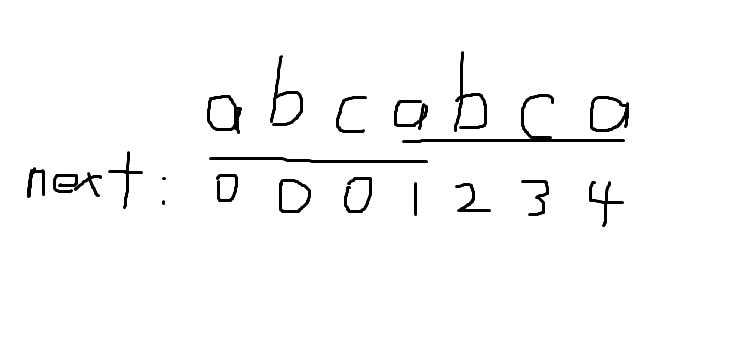
如图，对于$abcabca$，因为$next$数组表示的是非前缀子串与前缀子串匹配，$abc$找不到一个非本身后缀与非本身前缀对应，所以它们的$next$值就为$0$，而$abca$中的第一个$a$与最后一个$a$可以匹配，所以$next[4]=1$，而$abcabca$中后缀$abca$与前缀$abca$匹配，所以$next[7]=4$。
而AC自动机也有一个类似的$next$数组，但其并不是在线性结构上搞，而是将其存进一个类似于$trie$树的结构。这个结构长这样：
就比如，我们把$abc$和$aaa$存进这个结构：

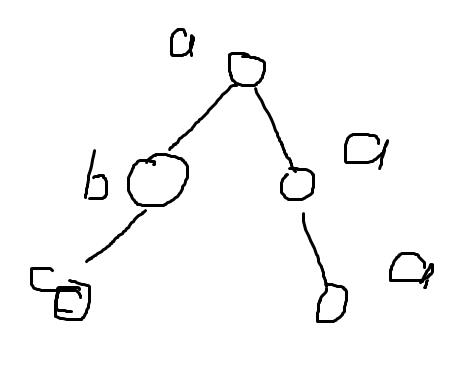
画得不好看。。。
也就是说，第一层对应的是所有字符串中第一位的字符，对于重复出现的，我们只存一个点，第二层，第三层也是如此。
然后，这个$next$数组，抽象点说，对应的不只是本串的最大前缀了，而是整个AC自动机所存的最大前缀。上图：

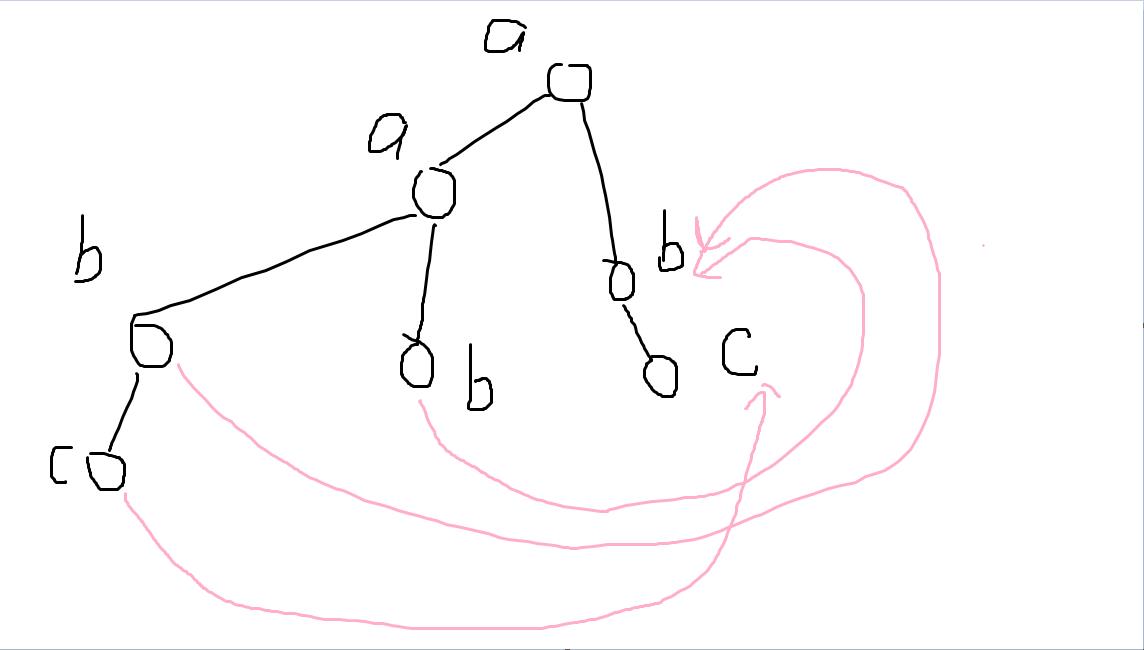
我们将$aabc$和$aab$以及$abc$存进了AC自动机里去，对于$aabc$，其后缀的最大前缀对应了$abc$
，$aab$的后缀对应了$ab$，所以，$next$数组实际上也就在AC自动机的图上加上了对应关系。
附上一段建图的代码：

#include<bits/stdc++.h>//存进n个字符串
using namespace std;
const int N=1e4+10;
const int S=26;
int nex[N*S],q[N*S],tr[N*S][S],n,idx,cnt[N*S];
char s[1000010];
void insert()//插入
{
	int p=0;
	for(int i=1;s[i];i++)
	{
		int j=s[i]-'a';
		if(!tr[p][j]) tr[p][j]=++idx;//当前节点下没有要存的点，再开一个 
		p=tr[p][j];
	}
	cnt[p]++;//某一个字符串已经存完 
}
void build()//建next数组
{
	int l=1,r=0;
	for(int i=0;i<26;i++)
	if(tr[0][i]) q[++r]=tr[0][i];//bfs 
	while(l<=r)
	{
		int t=q[l++];
		for(int i=0;i<S;i++)
		{
			if(!tr[t][i]) continue;
			int c=tr[t][i];
			int j=nex[t];
			while(j&&!tr[j][i]) j=nex[j];//找nex 
			if(tr[j][i]) j=tr[j][i];
			nex[c]=j;
			q[++r]=c;
		}
	}
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s+1);
		insert();
	}
	build();
	return 0;
}

注：上述代码只负责建图。
这里还有一段$fail$优化后的建图代码（对应的还有$fail$树这一结构，本次先不讲）：

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10,S=26;
int tr[N*S][S],cnt[N*S],idx,n,q[N*S],nex[N*S];
char s[1000001];
void insert()
{
	int p=0;
	for(int i=1;s[i];i++)
	{
		int t=s[i]-'a';
		if(!tr[p][t]) tr[p][t]=++idx;
		p=tr[p][t];
	}
	cnt[p]++;
}
void build()
{
	int l=1,r=0;
	for(int i=0;i<S;i++)
	if(tr[0][i]) q[++r]=tr[0][i];
	while(l<=r)
	{
		int o=q[l++];
		for(int i=0;i<S;i++)
		{
			int c=tr[o][i];
			if(!c)
			tr[o][i]=tr[nex[o]][i];//!!注意，这里不一样。 
			else
			{
				nex[c]=tr[nex[o]][i];
				q[++r]=c;
			}
		}
	}
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s+1);
		insert();
	}
	build();
	scanf("%s",s+1);
	return 0;
}

两处代码不一样的地方就在于$next$数组找相同前缀时的向前跳跃，优化代码是为了跳一次就找到可以停下来的节点。优化思想：将处理过的信息存下，当前向下找若没有对应的点，便存上一个点的信息，这样，每次指针向上跳跃只用跳一次就足够了。
AC自动机是多模匹配算法，用于处理多个字符串的信息。
emmmm。。。博客更新结束。