动态规划(Dynamic Programming)
Posted 楠c
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划(Dynamic Programming)相关的知识,希望对你有一定的参考价值。
目录
动态规划是分治思想的延伸,就像之前的递归一样,大问题分解成小问题。
但是递归有个不好的地方,对于复杂问题时间,空间复杂度十分的高,结果也不会保存。
比如:快速排序,没有三数取中优化的话,会导致栈溢出。
所以动态规划一般都是采用非递归,而且结果可以保存,这就是他们本质的区别。
动态规划特点:
- 把原来的问题分解成几个相似的子问题
- 所有的子问题只需解决一次
- 储存子问题的解
动态规划的本质,是对问题状态的定义和状态转移方程的定义(状态以及状态之间的递推关系)
所以动规问题一般从以四下个角度考虑:
- 状态定义
- 状态之间的转移方程定义
- 状态的初始化
- 返回结果
定义的状态一定要形成递推关系。三个特点,四个要素,两个本质
当问题看到这样的场景就可以考虑动态规划:
- 最大值、最小值
- 可不可行
- 是不是
- 方案个数
斐波那契数列

递归解法
假如递归来算的话,空间复杂度O(N),时间复杂度O(2^n),对数字非常敏感,所以数字大的时候是不可取的
class Solution {
public:
int Fibonacci(int n) {
if(n==0)
return 0;
if(n==1||n==2)
{
return 1;
}
return Fibonacci(n-1)+Fibonacci(n-2);
}
};
动态规划解法
问题: 数列第N项的值。
问题状态F(i): 数列第i项的值
转移方程: F(i)=F(i-1)+F(i-2)
初始状态: 方程中两个状态,F(0)=0,F(1)=1
返回结果 :F(N)
用数组保存之前的结果,之后用到直接从数组拿。
class Solution {
public:
int Fibonacci(int n) {
vector<int> F(n+1,0);
F[1]=1;
for(int i=2;i<n+1;i++)
{
F[i]=F[i-1]+F[i-2];
}
return F[n];
}
};
而它的时间复杂度O(N),空间复杂度也是O(N)
优化空间
由于不需要保存所有子问题的解,只需要两个变量来保存相邻的两项,不断地更新这两个变量就好.
class Solution {
public:
int Fibonacci(int n) {
//F[n-2]
int Fn2=0;
//F[n-1]
int Fn1=1;
int Fn=0;
if(n<=0)
return 0;
if(n==1)
return 1;
for(int i=2;i<=n;i++)
{
Fn=Fn1+Fn2;
Fn2=Fn1;
Fn1=Fn;
}
return Fn;
}
};
时间复杂度O(N),空间复杂度O(1)
变态青蛙跳台阶

问题:跳上n级台阶方法的个数。(并没有说你跳上n级台阶方法具体是怎么样的)

问题状态F[i]:跳上第i级台阶方法的个数


状态转移方程: F[i]=2F[i-1]
初始状态:

返回结果:F[N]
然后计算2的n-1次方就好。
排列的思想也可以
每个台阶看成一个位置,除过最后一个位置,其它位置都有两种可能性,
所以总的排列数为2^(n-1)*1 = 2^(n-1)
class Solution {
public:
int jumpFloorII(int number) {
if(number<=0)
return 0;
int ret=1;
for(int i=1;i<number;i++)
{
ret*=2;
}
return ret;
}
};
也可以用移位,时间复杂度O(1)
class Solution {
public:
int jumpFloorII(int number) {
if(number<=0)
return 0;
return 1<<(number-1);
}
};
扩展1:
上述问题为变态青蛙跳台阶。现在让它变成一个正常的青蛙,限制它
一次只能跳1阶或者2阶,求跳到第n阶的方法。
F[i]=F[i-1]+F[i-2]
扩展2:矩形覆盖
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。
请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
问题状态:用i个小矩形覆盖2*i个大矩形,求方法个数
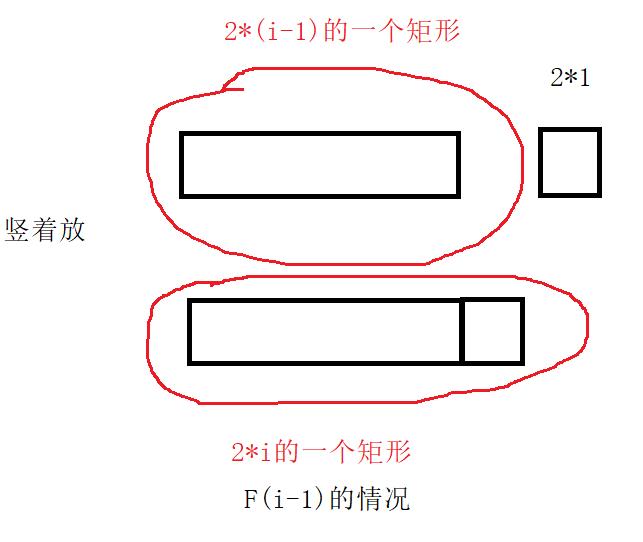
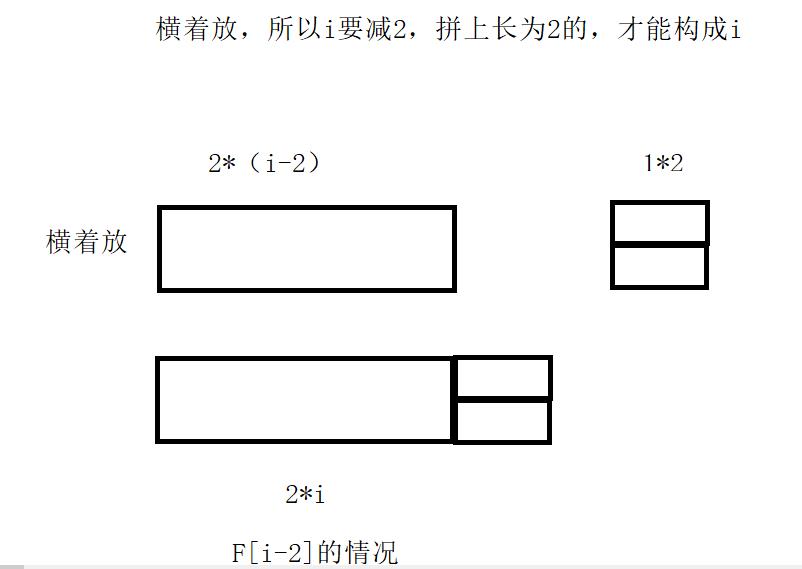
将他们看成两种情况,两种情况构成两种不同的方法
转移方程:F(i-1)+F(i-2)
求最大连续子序列的和

假如全为正数,全部累加就是最大。
问题:求数组最大连续和
子问题:局部元素构成的数组,他的最大连续和
问题状态:前i个元素组成的数组,他的最大连续子序列的和

重新定义问题状态:以第i个元素结尾的最大子序列的和
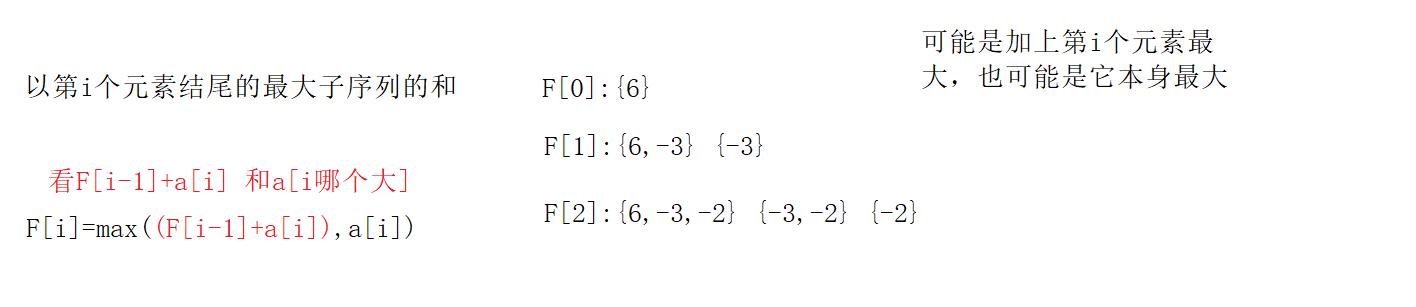
状态转移方程:F(i)=max(F(i-1)+a[i],a[i]),求出加上那个元素大,还是他自己本身大,F[i]不是最终结果,需要最后比较)
初始状态:F(0)=a[0]
返回值:返回值并不是最大的,需要在F[i]里面选出最大的那一个。
即dp[i],是以第i个元素结尾的最大子序和。需要找出dp[i]中最大的一个。
普通解法
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n=nums.size();
if(n==0)
return 0;
vector<int> dp(n,0);
dp[0]=nums[0];
int maxN=nums[0];
for(int i=1;i<n;i++)
{
dp[i]=max(dp[i-1]+nums[i],nums[i]);
maxN=maxN>dp[i]?maxN:dp[i];
}
return maxN;
}
};
优化空间
以前的dp[i]是不用关心的,只关心上一个dp[i-1],所以用一个变量来保存上一个dp[i-1],每次更新即可。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n=nums.size();
if(n==0)
return 0;
int maxV=nums[0];
int maxN=0;
for(int i=0;i<n;i++)
{
maxN=max(nums[i],maxN+nums[i]);
maxV=maxV>maxN?maxV:maxN;
}
return maxN;
}
};
单词拆分

普通解法
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> dict(wordDict.begin(),wordDict.end());
if(dict.size()==0||s.size()==0)
return false;
int n=s.size();
vector<bool> dp(n+1);
dp[0]=true;
for(int i=1;i<=n;++i)
{
for(int j=0;j<i;++j)
{
//可以就退出
if(dp[j] && (dict.find(s.substr(j,i-j)))!=dict.end())
{
dp[i]=true;
break;
}
}
}
return dp[n];
}
};
三角型最小路径和
普通解法

class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
//拷贝构造
vector<vector<int>> dp(triangle);
int row=triangle.size();
//int col=triangle.size();
for(int i=1;i<row;i++)
{
//第二行(下标为1),两个元素,0<=1循环就会处理两个元素。第三次
//for(int j=0;j<triangle.size();j++);第二次太麻烦了
//for(int j=0;j<col;j++);第一次写错了
for(int j=0;j<=i;j++)
{
//边界处理
if(j==0)
dp[i][j]=dp[i-1][j]+triangle[i][j];
else if(i==j)
dp[i][j]=dp[i-1][j-1]+triangle[i][j];
else
dp[i][j]=min(dp[i-1][j],dp[i-1][j-1])+triangle[i][j];
}
}
//第四行有4列元素,自顶向下,到这四个元素那个小,就是哪个
//先确定最后一行第一个元素
int minN=dp[row-1][0];
//即遍历最后一行的dp数组,由于行数等于列数,所以row
for(int j=0;j<row;j++)
{
minN=minN<dp[row-1][j]?minN:dp[row-1][j];
}
return minN;
}
};
自底向上优化

class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
vector<vector<int>> dp(triangle);
int row=triangle.size();
//自底向上
//row=4,i=2,从第3行(下标为2)开始,i=2,j=2,
//...
for(int i=row-2;i>=0;--i)
{
for(int j=0;j<=i;j++)
{
dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j];
}
}
return dp[0][0];
}
};
路径总数

class Solution {
public:
/**
*
* @param m int整型
* @param n int整型
* @return int整型
*/
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m,vector<int>(n,1));
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
有障碍的路径总数
和上一题差不多,只不过加入了障碍,当他们为最上,和最左两个边界时,只要遇到有障碍,就必须停止赋1操作。其他情况递推时,当前没有障碍递推即可。
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m=obstacleGrid.size();
int n=obstacleGrid[0].size();
vector<vector<int>> dp(m,vector<int>(n,0));
//一个有障碍,整条路径都只能为0,即停止赋1操作
for(int i=0;i<m && obstacleGrid[i][0]==0;++i)
{
dp[i][0]=1;
}
for(int i=0;i<n && obstacleGrid[0][i]==0;++i)
{
dp[0][i]=1;
}
//没有障碍时,才能计算dp[i][j]
for(int i=1;i<m;++i)
{
for(int j=1;j<n;j++)
{
if(obstacleGrid[i][j]==0)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
};
最小路径和

class Solution {
public:
/**
*
* @param grid int整型vector<vector<>>
* @return int整型
*/
int minPathSum(vector<vector<int> >& grid) {
int m=grid.size();
int n=grid[0].size();
vector<vector<int>> dp(grid);
for(int i=1;i<m;i++)
{
dp[i][0]=dp[i-1][0]+grid[i][0];
}
for(int j=1;j<n;j++)
{
dp[0][j]=dp[0][j-1]+grid[0][j];
}
for(int i=1;i<m;i++)
{
for(int j