分割回文串，编辑距离，不同子序列

Posted 2021-07-04 楠c

目录

• 分割回文串
• • 普通解法
  • 优化时间
• 编辑距离
• • 普通解法
• 不同子序列
• • 普通解法
  • 优化空间

分割回文串

普通解法

class Solution {
private:
    //O(n^3)差点超时
    bool isPal(const string& s,int left,int right)
    {
        while(left<right)
        {
            if(s[left]!=s[right])
              return false;
            left++;
            right--;
        }
              return true;
    }
public:
    int minCut(string s) {
       int n=s.size();
       vector<int> dp(n+1,0);
       for(int i=0;i<=n;++i)
       {
           dp[i]=i-1;
       }
       for(int i=1;i<=n;++i)
       {
           for(int j=0;j<i;++j)
           {
               if(isPal(s,j,i-1))
               {
                   dp[i]=min(dp[i],dp[j]+1);
               }
           }
       }
       return dp[n];
    }
};

因为判断回文串是个O(N)的函数

优化时间

判断回文串也是一个动态规划问题

提前将它算好，需要判断的时候传入区间，直接取出结果，两个N^2的算法，时间复杂度O(N^2)

class Solution {
public:
    int minCut(string s) {
       int n=s.size();
       vector<int> dp(n+1,0);
       for(int i=0;i<=n;++i)
       {
           dp[i]=i-1;
       }
       //这个就开成大小一样，0就对应下标0，第一个元素，
       vector<vector<bool>> isPal(n,vector<bool>(n,false));
       //判断是否为回文串的动态规划
       //看两侧是否为回文串，是的话缩小两边，判断去掉两边后是否为回文串
       //所以要从后向前走
       for(int i=n-1;i>=0;--i)
       {
           for(int j=i;j<n;++j)
           {
                //j=i，即当一个字符时
                if(i==j)
                {
                  isPal[i][j]=true;
                }
                else if(i+1==j)//j+1==i时，两个字符时只要相等就是回文
                {
                   isPal[i][j]=(s[i]==s[j]); 
                }                
                else//两个字符以上
                {
                   isPal[i][j]=(s[i]==s[j])&&(isPal[i+1][j-1]);
                }
           }       
       } 
       
       //判断次数的动态规划
       for(int i=1;i<=n;++i)
       {
           for(int j=0;j<i;++j)
           {
               //是回文串，次数+1，然后和上一个的次数相比看哪个小

               //如果第j+1和i元素为回文串，才能去算第i个元素
               if(isPal[j][i-1])//因为dp多开了一个，isPal没有多开
               {
                   dp[i]=min(dp[i],dp[j]+1);
               }
           }
       }
       return dp[n];
    }
};

效率高了很多

编辑距离

画图来仔细理解一下

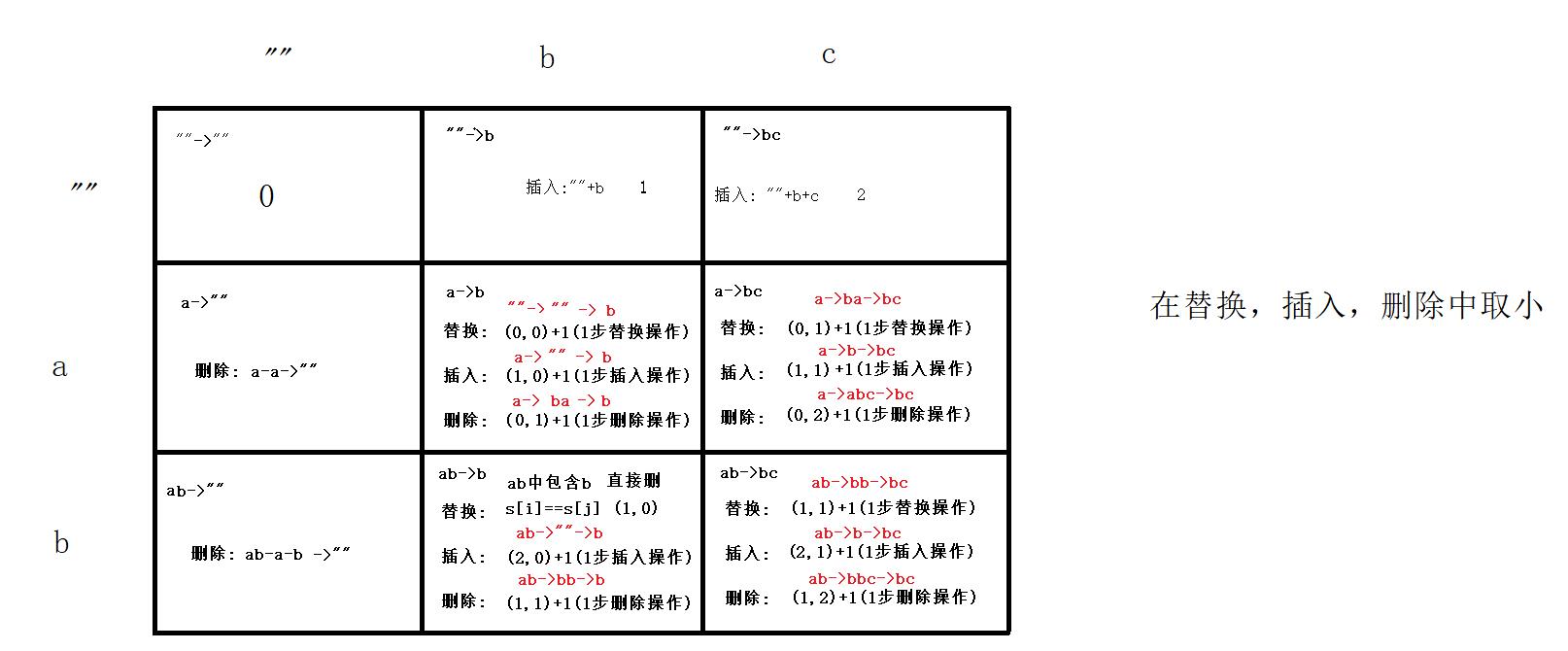
普通解法

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1=word1.size();
        int len2=word2.size();
        
        vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));
        //初始化删除操作
        for(int i=0;i<=len1;++i)
        {
           dp[i][0]=i;
        }
        //初始化插入操作
        for(int i=0;i<=len2;++i)
        {
            dp[0][i]=i;
        }

        for(int i=1;i<=len1;++i)
        {
            for(int j=1;j<=len2;++j)
            {
                //插入和删除取小
                dp[i][j]=min(dp[i-1][j],dp[i][j-1])+1;
                
                //替换有两种情况
                //1.相等不用多考虑，直接用dp[i-1][j-1]的操作
                if(word1[i-1]==word2[j-1])
                {   
                    dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
                }
                else//2.不相等,用dp[i-1][j-1]的操作不够,还要+1(多1步替换操作)
                {
                    dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);
                }
            }
        }

        return dp[len1][len2];
    }
};

不同子序列

画图仔细理解过程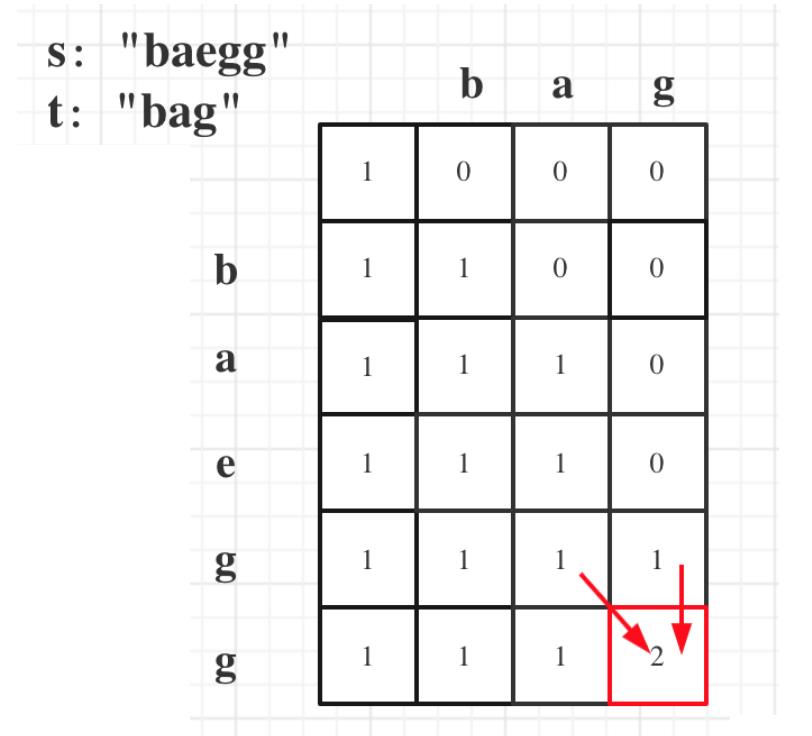

普通解法

class Solution {
public:
    /**
     * 
     * @param S string字符串 
     * @param T string字符串 
     * @return int整型
     */
    int numDistinct(string S, string T) {
        int len1=S.size();
        int len2=T.size();
        vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));
        
        //即S的前i个字符和空串的子序列个数
        //空集是每个前i个字符的子集,然后空集和空集相同即初始化为1个
        for(int i=0;i<=len1;i++)
        {
         dp[i][0]=1;
        }
        //dp[0][j]呢？昏头了，S的前0个字符，即空集和前j个字符的子集，那肯定不能初始化
        for(int i=1;i<=len1;++i)
        {
            for(int j=1;j<=len2;++j)
            {
                if(S[i-1]==T[j-1])
                {
                            //不利用S[j-1]+利用S[j-1]
                    dp[i][j]=dp[i-1][j]+dp[i-1][j-1];
                }
                else
                {   //没得选，只能不利用
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[len1][len2];
    }
};

优化空间

类似于背包问题的优化空间，需要记住从后向前递推

class Solution {
public:

    int numDistinct(string S, string T) {
        int n=S.size();
        int m=T.size();
        vector<int> dp(m+1,0);
        
        dp[0]=1;
        
        for(int i=1;i<=n;++i)
        {
            //优化时类似于背包的从后往前
            for(int j=m;j>0;--j)
            {
                //相等，不利用S[j-1]+利用S[j-1]
                if(S[i-1]==T[j-1])
                {
                    dp[j]=dp[j]+dp[j-1];
                }
                /*else
                {
                    dp[j]=dp[j];
                }*/
            }
        }
        return dp[m];
    }
};