在排序数组中查找元素的第一个和最后一个位置

Posted 2021-07-04 炫云云

在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

进阶：

你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗？

示例 1：

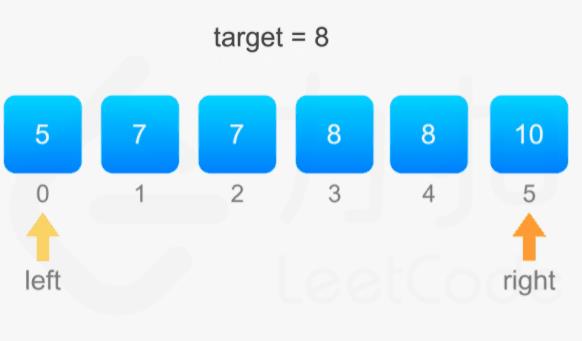
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

思路与算法 : 二分查找

直观的思路肯定是从前往后遍历一遍。用两个变量记录第一次和最后一次遇见 $\text{target}$ 的下标，但这个方法的时间复杂度为 $O(n)$ ，没有利用到数组升序排列的条件。

由于数组已经排序，因此整个数组是单调递增的，我们可以利用二分法来加速查找的过程。

• 第 1 部分：查找 target 出现的第 1 个位置,这部分代码上面已经讲过了
• 第 2 部分：查找 target 出现的最后 1 个位置,这部分代码上面已经讲过了。
• 补充完整的代码

class Solution(object):
    def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        if len(nums) ==0:
            return [-1,-1]
        leftIdx = self.findFirstPosition(nums, target)
        if leftIdx== -1:
            return [-1,-1]
        rightIdx = self.findLastPosition(nums, target)
        return [leftIdx,rightIdx]

    # 寻找最后一个位置
    def findLastPosition(self,nums, target):
        # 左右都闭合的区间 [l, r]
        l, r = 0, len(nums) - 1
        while l <= r:
            mid = int(l + (r - l) / 2) # 防止计算时溢出
            if nums[mid] == target:
                # 只有这里不一样：不可以直接返回，应该继续向右边找，即 [mid + 1, right] 区间里找
                # 收缩左边界
                l = mid + 1;
            # 应该继续向右边找,搜索区间变为 [mid+1, right]
            elif nums[mid] < target: 
                l = mid + 1
            # 应该继续向左边找,搜索区间变为 [left, mid - 1]
            elif nums[mid] > target: 
                r = mid - 1
        if r < 0 or nums[r] != target: return -1
        return r

    def findFirstPosition(self,nums, target):
        l, r = 0, len(nums) - 1
        while l <= r:
            mid = int(l + (r - l) / 2) # 防止计算时溢出
            if nums[mid] == target:
                # ① 不可以直接返回，应该继续向左边找，即 [left，mid - 1] 区间里找
                # 收缩右边界
                r = mid - 1;
            elif nums[mid] < target:  # 应该继续向右边找,搜索区间变为 [mid+1, right]
                l = mid + 1
            else: #  nums[mid] > target ,应该继续向左边找 ,搜索区间变为 [left, mid - 1]
                r = mid - 1
        # 此时 left 和 right 的位置关系是 [right, left]，注意上面的 ①，此时 left 才是第 1 次元素出现的位置
        # 因此还需要特别做一次判断
        if l >= len(nums) or nums[l] != target: 
            return -1
        return l

a = Solution()
print(a.searchRange( nums = [5,7,7,8,8,10], target = 8))

[3, 4]

考虑 $\text{target}$ 开始和结束位置，其实我们要找的就是数组中「第一个等于 $\text{target}$ 的位置」（记为 $\text{leftIdx}$ ）和「第一个大于 $\text{target}$ 的位置减一」（记为 $\text{rightIdx}$）。

定义一个二分查找，寻找 $\text{leftIdx}$ 即为在数组中寻找第一个等于 $\text{target}$ 的下标，寻找 $\text{rightIdx}$ 即为在数组中寻找第一个大于 $\text{target}$ 的下标，然后将下标减一,即为最后一个位置。

最后，因为 $\text{target}$ 可能不存在数组中，因此我们需要重新校验我们得到的两个下标 $\text{leftIdx}$ 和 $\text{rightIdx}$，看是否符合条件，如果符合条件就返回 $[\text{leftIdx},\text{rightIdx}]$ ，不符合就返回 $[-1,-1]$ 。

class Solution(object):
    def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        def binarySearch(nums, target):
            left = 0
            right = len(nums) -1
            while(left<=right):
                mid = left +  (right-left) //2
                if nums[mid]>=target:  #应该继续向左边找 ,搜索区间变为 [left, mid - 1]
                    right = mid-1      #寻找第一个满足条件的点， 即使得right在满足target的数的最左边
                else:                 
                    left = mid+1       # 应该继续向右边找,搜索区间变为 [mid+1, right]
            return left
            
        leftIdx = binarySearch(nums, target)
        rightIdx = binarySearch(nums, target+1) -1

        if leftIdx == len(nums) or nums[leftIdx] !=target:
            return [-1,-1]
        else:
            return [leftIdx,rightIdx]

a = Solution()
a.searchRange(nums = [1,3], target = 1)

[0, 0]

为了代码的复用，我们定义 binarySearch(nums, target, lower) 表示在 $\text{nums}$ 数组中二分查找 $\text{target}$ 的位置，如果 $\text{lower}$ 为 $\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}$ ，则查找第一个等于 $\text{target}$ 的下标，即寻找左侧边界。否则查找第一个大于$\text{target}$ 的下标，-1为寻找右侧边界。

最后，因为 $\text{target}$ 可能不存在数组中，因此我们需要重新校验我们得到的两个下标 $\text{leftIdx}$ 和 $\text{rightIdx}$，看是否符合条件，如果符合条件就返回 $[\text{leftIdx},\text{rightIdx}]$ ，不符合就返回 $[-1,-1]$.

class Solution(object):
    def searchRange(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        def binarySearch(nums, target,lower):
            left = 0
            right = len(nums) -1
            ans=len(nums)
            while(left<=right):
                mid = left +  (right-left) //2
                if (nums[mid]>target or (lower and nums[mid] >=target)):
                    right = mid-1
                    ans = mid
                else:
                    left = mid+1
            return ans
            
        leftIdx = binarySearch(nums, target,True)
        rightIdx = binarySearch(nums, target,False) -1

        if (leftIdx <= rightIdx and rightIdx < len(nums) and nums[leftIdx] == target and nums[rightIdx] == target):
            return [leftIdx,rightIdx]

        return [-1,-1]

计算过程：