并查集解决图论问题（连通性及有无圈存在）

Posted 2021-07-04 秦枫-_-

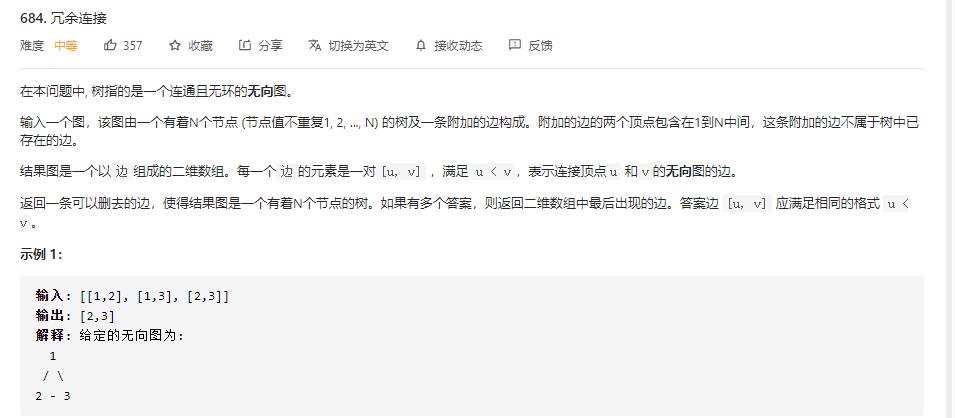
题目中确定给的是连通图，那么根据图论知识树的等价条件为m=n-1，所以很明显数组中只有一条边是答案，同时只要找出来图中的一个圈就能得到答案，树是无圈连通图，那么可以用并查集思想解题

回想图论找出最小生成树 有避圈法和破圈法，本题用避圈法思想

遍历数组，对于每一条边的两个点 ，在这条边之前构造的图中，如果两点已连通，加上这条边就有圈，就必然不是树，所以这条边就是答案

如果两点不连通，加上这条边则为树，继续下去找最大树

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
    int []parent=new int[edges.length+1];
    for(int i=1;i<=edges.length;i++){
     parent[i]=i;
    }
    for(int i=0;i<edges.length;i++){
        if(find(parent,edges[i][0])!=find(parent,edges[i][1])){
            link(parent,edges[i][0],edges[i][1]);
        }
        else
        return edges[i];
    }
    return new int[0];
    }
    public void link(int []parent,int point1,int point2){
         parent[parent[point1]]=find(parent,point2);//key:point1和它的parent已经连通了，所以只要parent[point1]和point[2]连通
    }
    public int find(int []parent,int point){
        if(parent[point]!=point){
            parent[point]=find(parent,parent[point]);
        }
        return parent[point];

    }
}