算法2-1前缀和与差分

Posted 2021-07-02 幽殇默

目录

• P1115 最大子段和
• P3397 地毯
• P1719 最大加权矩形 【前缀和标准模板题】

P1115 最大子段和

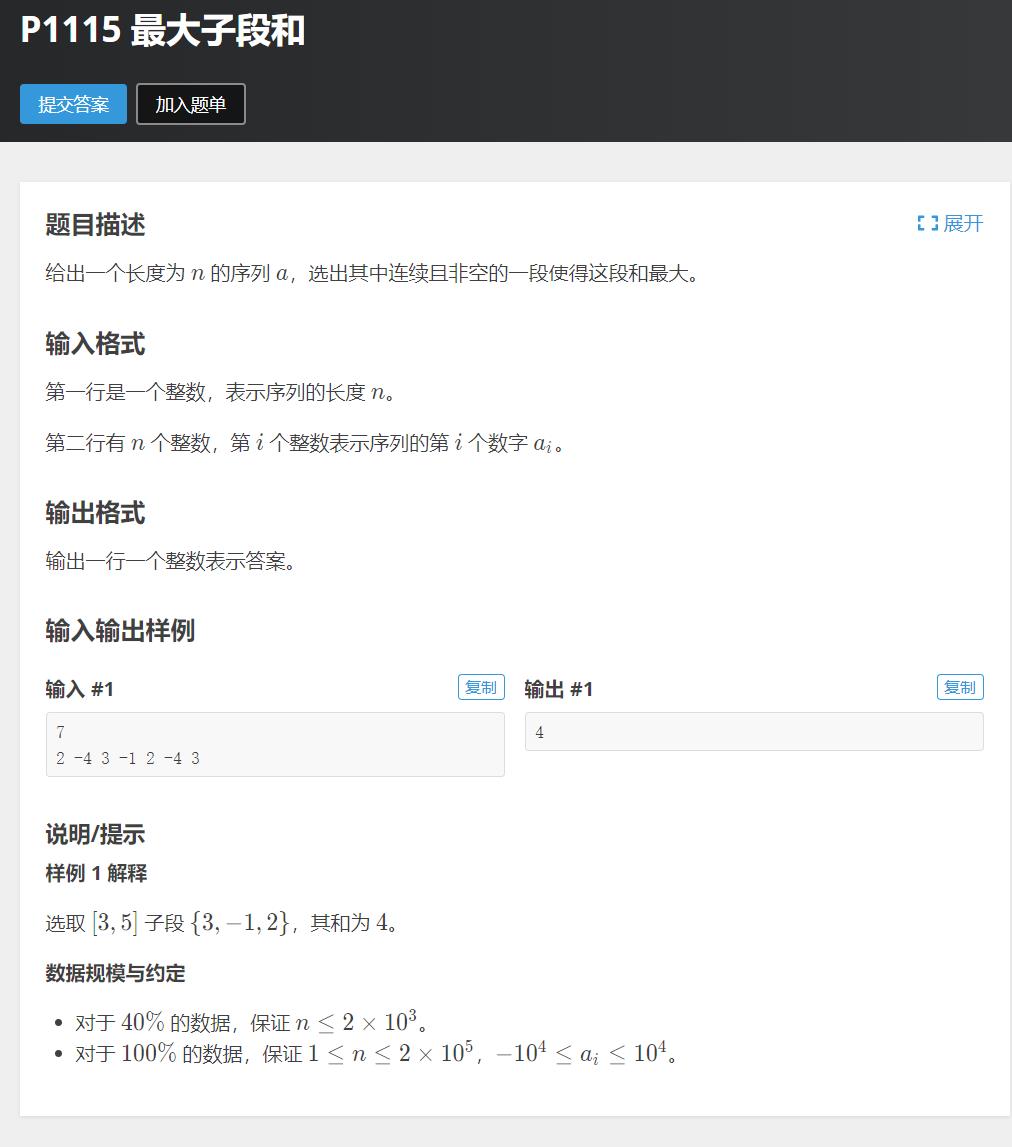
https://www.luogu.com.cn/problem/P1115

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int main(void)
{
	int n; cin>>n;
	int ans=-99999;
	int sum=0;
	while(n--)
	{
		int x; cin>>x;
		sum+=x;
		if(sum>ans) ans=sum;
		if(sum<0) sum=0;
	}
	cout<<ans<<endl;
	return 0;
}

P3397 地毯

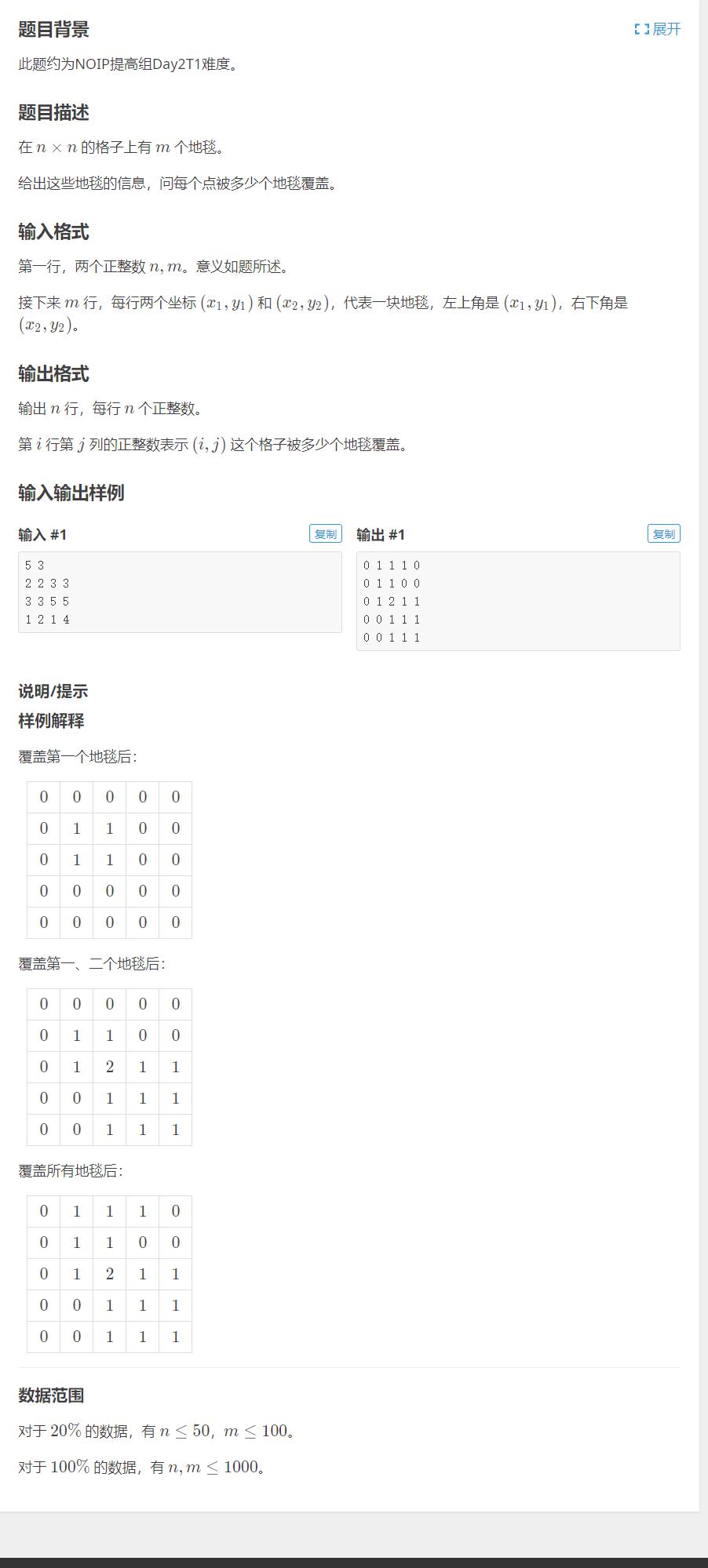
https://www.luogu.com.cn/problem/P3397

#include<cstdio>
#include<iostream>
using namespace std;
int a[1005][1005];
int n,m;
int main(void)
{
	cin>>n>>m;
	while(m--)
	{
		int x,y,xx,yy; cin>>x>>y>>xx>>yy;
		for(int i=x;i<=xx;i++)
		{
			for(int j=y;j<=yy;j++)
			{
				a[i][j]++;
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			cout<<a[i][j]<<" ";
		}
		cout<<endl;
	}
	return 0;
}

P1719 最大加权矩形 【前缀和标准模板题】

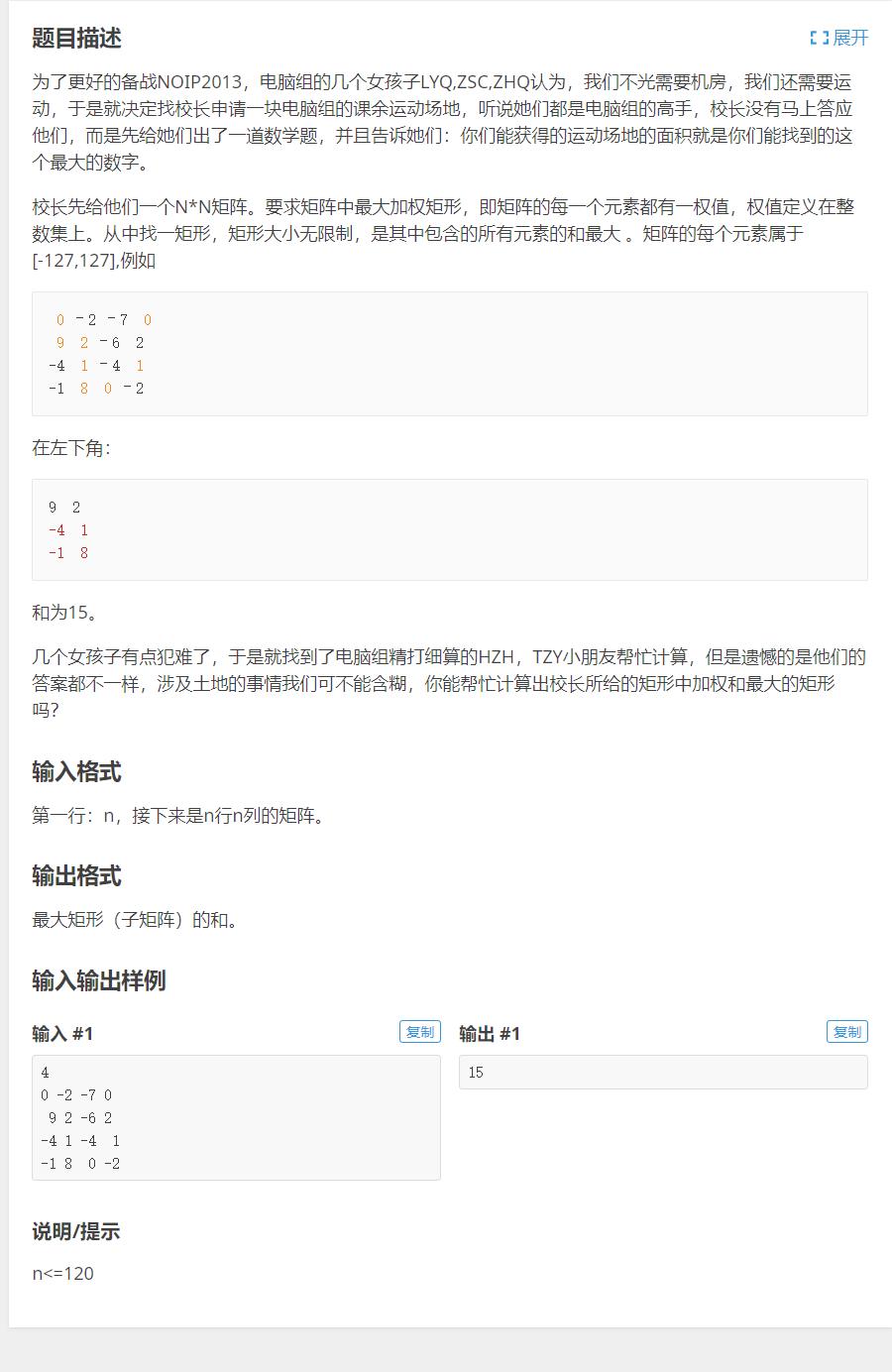
https://www.luogu.com.cn/problem/P1719

朴素做法: 得开o2加速 最后一个点才能过。
因为重复的算了两遍。 左上角，右下角。 左下角和右上角。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int a[130][130];
int s[130][130];
long long int ans=-1e9;
int main(void) 
{
	int n; cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&a[i][j]);
			s[i][j]=s[i-1][j]+s[i][j-1]+-s[i-1][j-1]+a[i][j];
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			for(int k=1;k<=n;k++)
			{
				for(int w=1;w<=n;w++)
				{
					int x,y,xx,yy;
					x=min(i,k);y=min(j,w); xx=max(i,k);yy=max(j,w);
					long long int sum=s[xx][yy]-s[xx][y-1]-s[x-1][yy]+s[x-1][y-1];
					ans=max(ans,sum);
				}
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}

优化后的：

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int a[130][130];
int s[130][130];
long long int ans=-1e9;
int main(void) 
{
	int n; cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&a[i][j]);
			s[i][j]=s[i-1][j]+s[i][j-1]+-s[i-1][j-1]+a[i][j];
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			for(int k=1;k<=n;k++)
			{
				for(int w=1;w<=n;w++)
				{
					if(i>k||j>w) continue;// 不是左上角的坐标 和右下角的坐标  而是左下角的坐标和右上角的坐标
					int x,y,xx,yy;
					x=i,y=j,xx=k,yy=w;
					long long int sum=s[xx][yy]-s[xx][y-1]-s[x-1][yy]+s[x-1][y-1];
					ans=max(ans,sum);
				}
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}