从Paxos到Multi-Paxos
Posted 360云计算
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从Paxos到Multi-Paxos相关的知识,希望对你有一定的参考价值。
女主宣言
There is only one consensus protocol, and that's Paxos – all other approaches are just broken versions of Paxos.
PS:丰富的一线技术、多元化的表现形式,尽在“360云计算”,点关注哦!
1
简介
2
Paxos的引入
2.1 简介
如果要理解Paxos,那必须要知道Paxos解决了什么问题,当然在是解决一致性问题,这里想说的是Paxos如何去解决一致性问题,笔者查阅了论文和网上很多相关的文章,认为最易于记忆的总结是:
#确定一个不可变变量的取值
Paxos通过确定一个不可变变量的取值来使分布式系统达成一致,对于这个总结可能会存在不少疑惑,变量的意义是什么?为什么不可变?变量确定了有什么作用?系统中的数据都是变化的,随时可能发生增删改;但如果换另一个思路,在一份数据的多个副本中,假设它们的初始状态一致,如果对它们进行系统的操作并且操作的顺序一致,那副本在每个操作结束后的结果也就是一致的,这里我们把各个操作按照顺序记录成[op.1,op.2,...op.i,op.i+1,...],在一个分布式系统中,必然会存在多个进程同时对数据进行操作,那Paxos要做的就是在这些操作中进行选择,并将选择的结果赋值给op.i,这个过程称为确定,即确定op.i的值,一旦op.i确定后就不可再更改。
2.2 基本角色
-
Proposer: 提出需要被确定的值; -
Acceptor: 对提出的值进行确定; -
Learner: 将确定的值保存和应用;
在Paxos中,包括了三类角色,分别是Proposer、Accepter和Learner,一个系统中他们都存在一个或多个。需要被确定的值由Proposer提出,值被提出后发送给接收者Acceptor进行确定,确定成功后由学习者对值进行保存和应用。
2.3 确定一个值(单个Accptor)
图1
如图1,在只有单个Acceptor的系统中,对于多个Propser提出的多个值,Acceptor只要选择第一个到达的就能将值确定下来。相应的问题是单点Acceptor失效的情况下会使得系统不可用,所以需要引入多个Acceptor。
2.4 确定一个值(多个Accptor)
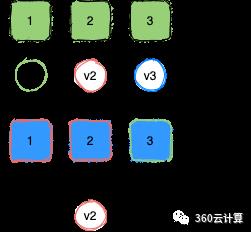
图2
如图2,在具有多个Acceptor的系统中,Proposer可以将提出的值发送给多个Acceptor,只要被大多数(一半以上)Acceptor接受了,那么值就被确定了。为什么是大多数?任何两个由大多数Acceptor组成的集合必然存在交集,即公共的Acceptor,**只要保证Acceptor只能接受(accept)一个值**,那任何两个大多数集合确定的值就是一样的,如果不一样,则集合交集中至少存在一个Acceptor接受了两个值,和条件违背,所以只要**大多数**Acceptor接受了一个值,那值就确定了,并且系统能供容忍少于大多数的Acceptor出现故障。综上,得出的Paxos实现一致性的原始条件是:
#Acceptor只能接受一个值

图3
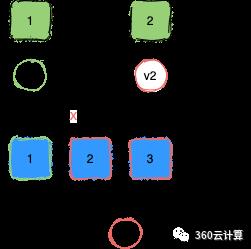
图4
如图4,如果一个Acceptor只能接受一个值,那就能保证在一个值被大多数Acceptor接受后就不会出现另一个值再被接受。
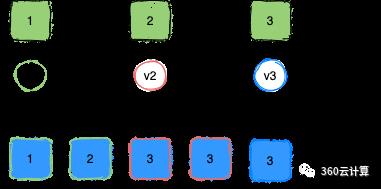
图5
#P2.如果一个值为v的提议被确定了,那之后确定的提议(提议号更高)的值(提议值)也是v
由于提议编号是有序递增的,该条件保证了一旦有提议被确定了,那之后被再确定的提议值是相同的,确保了只有一个值被确定。
一个提议在被Acceptor之前,需要被Proposer提出,只要满足P2b就能满足P2a。但Proposer如何如何确定提议的提议值v是什么?只要做到有确定的值就用确定值,没有则用自己的值,因此引入P2c。
#P2c.如果一个提议号为n,提议值为v的提议被一个Proposer提出,那必然存在一个由大多数Acceptor组成的集合S:
(a).集合S中的任何一个Acceptor都没有接受过提议号小于n的提议;
(b).v是集合S中的Acceptor接受的最高提议编号m对应的提议值,其中m<n;
#1.Proposer选择提议号n发送给Acceptor,并要求Acceptor对自身做如下的承诺:
(a).不再接受提议号小于n的提议
(b). 如果Acceptor已经接受了提议,则将提议返回给Proposer
这个过程称为prepare;
#2.如果Proposer接收到了大多数Acceptor的请求返回,那Proposer就能提出提议号为n,提议值为v的提议,其中v有如下两种可能:
(a).如果请求返回中存在提议,则v是所有返回中具有最高提议号的提议值
(b).如果不存在返回,则使用Proposer自己的提议值
这个过程称为accept。
以上是Proposer的提议流程,针对Acceptor,会收到来自Proposer的两类请求:prepare和accept,从上面的条件可以看出,Acceptor一旦做出承诺,则不会再接受提议号小于n的提议,所以我们对P1进行修正:
# P1a.如果Acceptor没有收到过大于n的prepare请求,则可以接受提议号为n的提议。
以上是针对accept阶段的约束,可以做进一步的优化;如果acceptor收到了一个提议编号为n的prepare请求,此时发现已经回复过了一个提议号比n更大的提议,通过以上的约束条件,知道即使acceptor收到编号为n的accept请求,也不会被接受,所以可以忽略该prepare请求不作回复,或则回复通知proposer不必再发起accept请求。
综上,需要acceptor记录两个东西:
承诺过的最高提议编号
接受过的具有最高提议号的提议
2.5 Paxos总结

图6
-
阶段一:
-
阶段二:
2.6 活锁
在上一小节的总结中,可以看到Paxos主要分成两个阶段来完成,Acceptor通过提议编号的大小确定是否接受提议,可能会存在一种场景,如下图7所示:

Proposer.1收到客户端的请求后发送编号为1的提议,preapare被1,2,3三个Acceptor接收;
同时Proposer.3收到客户端的请求后发送编号为2的提议,也被1,2,3三个Acceptor接收;
Propser.1收到提议1的大多数prepare请求响应后发出accept请求,因为acceptor已经接收了编号为2的prepare请求,所以会拒绝编号为1的accept请求;
由于系统没有确定接受的值,所以Proposer.1会提高自己的提议编号为3,并发送preapre请求,并导致了编号为2的accept请求被拒绝;
不断的重复以上的步骤,会导致系统中不能确定被接受的值;
上诉的这种现象称为“活锁”;解决的办法可以在Proposer中选出一个leader,由leader进行所有提议的提交,如下图8所示:
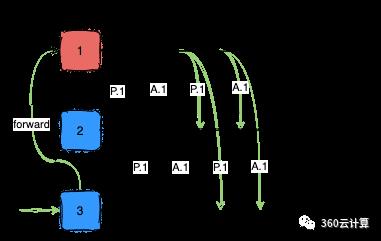
图8
3
Multi-Paxos
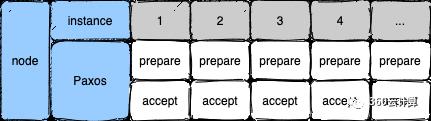
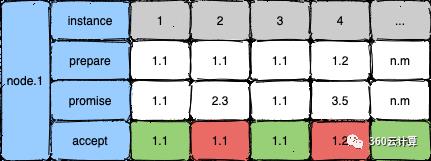
-
实例1中,节点1提出了编号为1的提议,顺利的被accept -
实例2中,节点2提出了编号为1的提议,由于节点1已经接收了来自节点2编号为3的提议,所以不会accept编号为1的提议;实例4同理,接收了来自节点3的更高的提议而导致1.2被拒绝;
4
总结
参考列表:
Paxos算法详解
深入理解Paxos算法协议
【原创】一步一步理解Paxos算法
Paxos、Multi-Paxos详解
paxos算法证明过程
Paxos理论介绍(1): 朴素Paxos算法理论推导与证明
以上是关于从Paxos到Multi-Paxos的主要内容,如果未能解决你的问题,请参考以下文章