ViP解读：视觉MLP结构新作

Posted 2021-07-01 周先森爱吃素

最近的一篇新的视觉MLP方面的工作，天津大学程明明组参与其中，通过充分利用2D特征图的位置信息设计的一个MLP结构ViP（Vision Permutator），获得了相当不错的性能。

简介

论文提出一种简单高效的类MLP结构，Vision Permutator，用于视觉识别任务。通过意识到2D特征图所携带的位置信息的重要性，因此，不同于之前的MLP模型总是沿着展平的空间维度编码空间信息，ViP通过线性投影的方式沿着高和宽两个维度编码特征表达。这使得ViP可以沿着某个空间方向捕获长程依赖并且同时在另一个方向保留精确的位置信息。通过这种方式获得的位置感知的输出特征以一个互相补充的方式聚合以形成感兴趣目标的有效表示。实验表明，ViP具有比肩CNN和视觉Transformer的能力。不需要2D卷积也不需要注意力机制，不使用额外的大尺度数据集，ViP仅仅通过25M的参数就取得了ImageNet上81.5的top-1精度，同等模型大小的约束下，这已经超越了大多数CNN和Transformer，更大版本的ViP精度更高，达到SOTA水准。

• 论文标题

  Vision Permutator: A Permutable MLP-Like Architecture for Visual Recognition

• 论文地址

  http://arxiv.org/abs/2106.12368

• 论文源码

  https://github.com/Andrew-Qibin/VisionPermutator

介绍

最近的MLP-Mixer和ResMLP证明了纯MLP结构也可以在图像分类等任务上表现得非常好。相比于卷积神经网络和视觉Transformer分别使用空域卷积和自注意力层来编码空间信息，类MLP网络只使用全连接层（或者1x1卷积），因此无论是训练还是测试都更加高效。但是，MLPs在图像分类上的优异表现往往得益于大尺度数据集的训练（如ImageNet-22K和JFT-300M），没有这些数据的支撑，其性能距离CNNs和Vision Transformers还有不小的差距。

这篇论文中，作者希望探索一个MLP结构仅仅使用ImageNet-1k数据集训练即可达到不错的效果，因此，提出了Vision Permutator结构（ViP）。具体而言是，Vision Permutator 通过提出一种新的层来创新现有的 MLP 架构，该结构可以基于基本矩阵乘法更有效地编码空间信息。 不同于现有的MLP模型，如MLP-Mixer和ResMLP，他们通过展平空间维度然后再线性投影来编码空间信息的，也就是说作用于尺寸为tokens x channels的张量上，这导致了2D特征图的位置信息丢失，ViP则保持了原始输入token的空间维度并沿着宽和高两个维度编码空间信息，这样可以保留充分的位置信息。

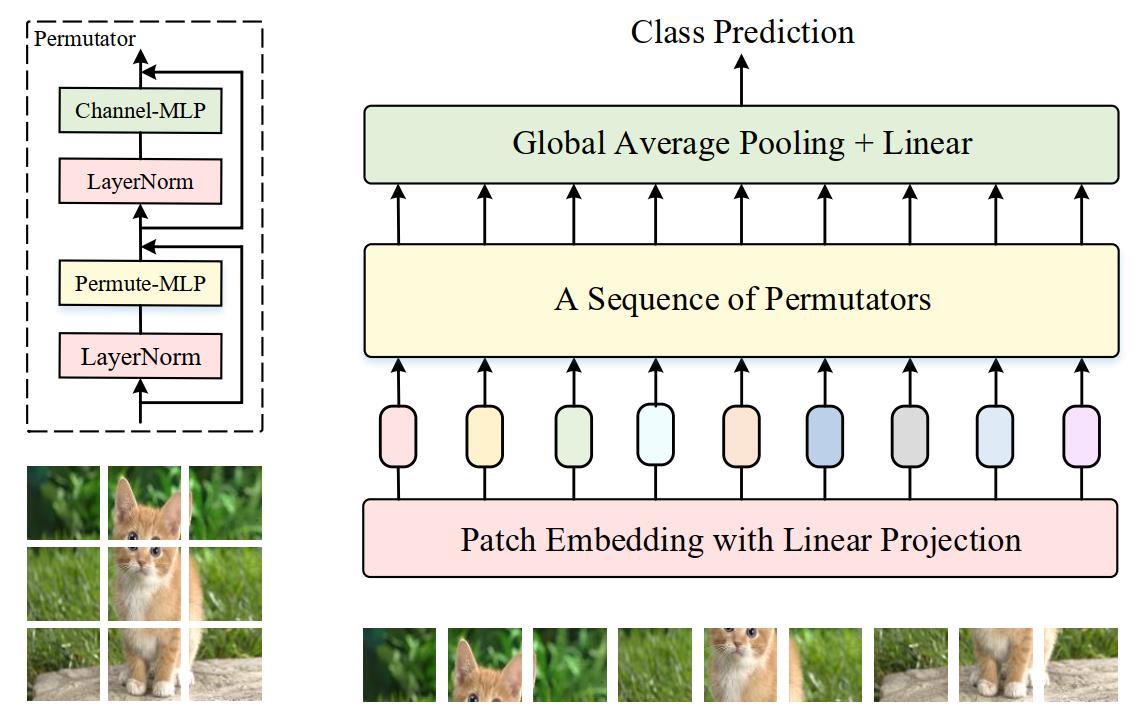
具体而言，和很多视觉Transformer结构类似，ViP首先通过对图像切块进行token化，将切得得小patch通过线性投影映射为token embedding，如上图所示。此时获得的token embedding的维度是height x width x channels，它们被送入一系列的Permutator block中，这个Permutator block包含一个用来编码空间信息的Permute-MLP和一个用来混合通道信息的Channel-MLP，这两个结构下文会详细介绍。随后经过这些block获得的特征会送入GAP和Linear层中用于图像分类任务。和现有的很多MLP结构混合两个空间方向信息的方式相比，ViP沿着不同的方向独立处理输入特征，保证token具有特定方向的信息，这已经被视觉中的很多方法证明是很重要的（如CoordAttention）。

ViP

ViP的整体结构如下图所示，该网络以224x224的图像作为输入并且将其均分为多个图像块（image patches），如14x14或7x7，这些图像块随后被映射为linear embedding（也叫token），这个映射通过一个共享的线性层完成，这和MLP-Mixer是一致的。

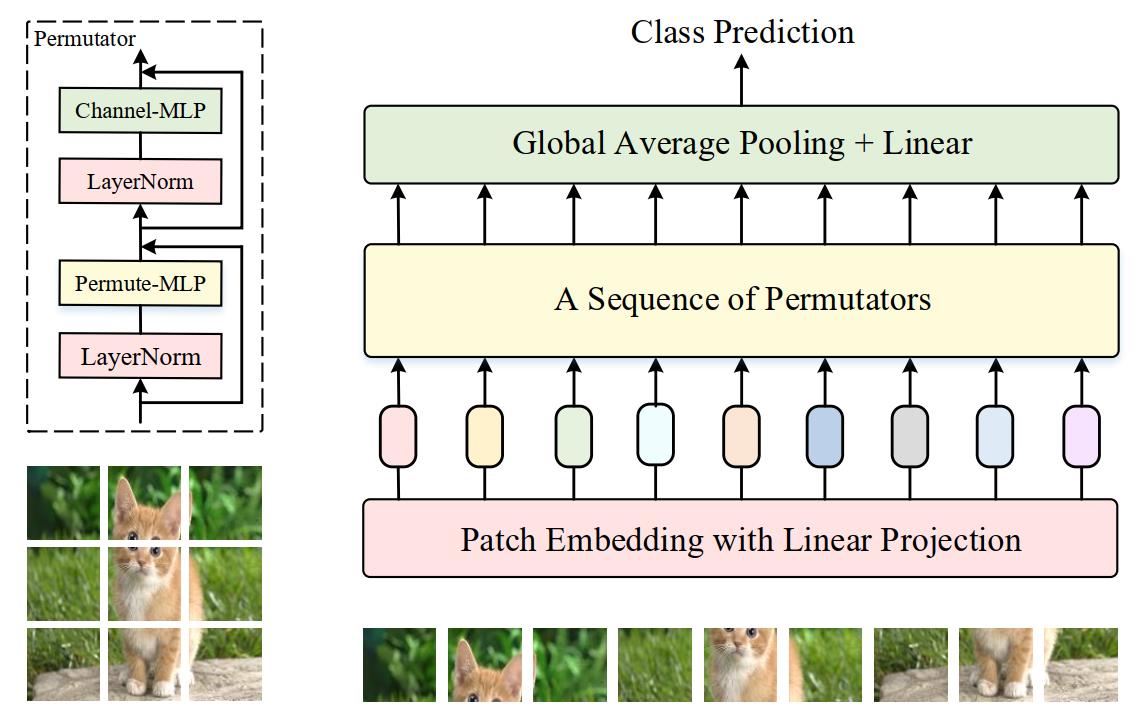
接着，这些token送入一序列的Permutator来编码空间和通道信息，产生的新token沿着空间维度做平均再用全连接层做分类。下文将详细描述核心的Permutator block以及网络的一些设置。

Permutator

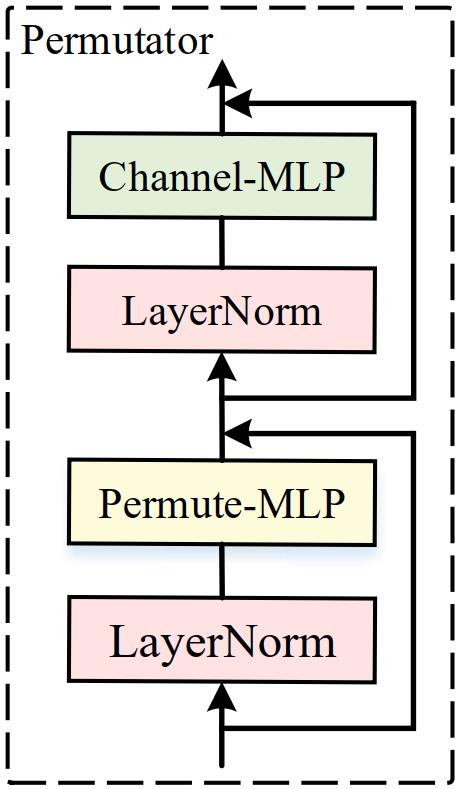
Permutator的结构如下图所示，如果不考虑用于标准化的LN和跳跃链接，这个结构的核心其实是两个组件：Permute-MLP和Channel-MLP，从名字上也知道，它们分别负责编码空间信息和通道信息。Channel-MLP和Transformer原论文中的前馈层结构类似，由两个全连接层中间夹着一个GELU激活函数。不过，关于空间信息的编码，最近的MLP-Mixer采用对输入token沿着空间维度进行线性投影的方式来处理，但是ViP则选择沿着高和宽两个方向分别处理。 数学上，对一个$C$维的输入tokens $\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$，Permutator的运算过程可以总结如下式，其中$LN$表示LayerNorm，输出的$\mathbf{Z}$则用于下一层block的输入。

$$\begin{array}{rl}& \mathbf{Y}=\text{ Permute-MLP }(\mathrm{L}\mathrm{N}(\mathbf{X}))+\mathbf{X}\\ & \mathbf{Z}=\text{ Channel-MLP }(\mathrm{LN}(\mathbf{Y}))+\mathbf{Y}\end{array}$$

由于Channel-MLP就是原始Transformer中的FFN结构，这里就不赘述了，下面来看这篇论文最核心的Permute-MLP。它的详细结构如下图所示，可以发现和之前视觉Transformer结构以及MLP-Mixer这类工作不一样的地方，它的输入其实不是二维的（即$tokens\times channels=HW\times C$），而是三维的。

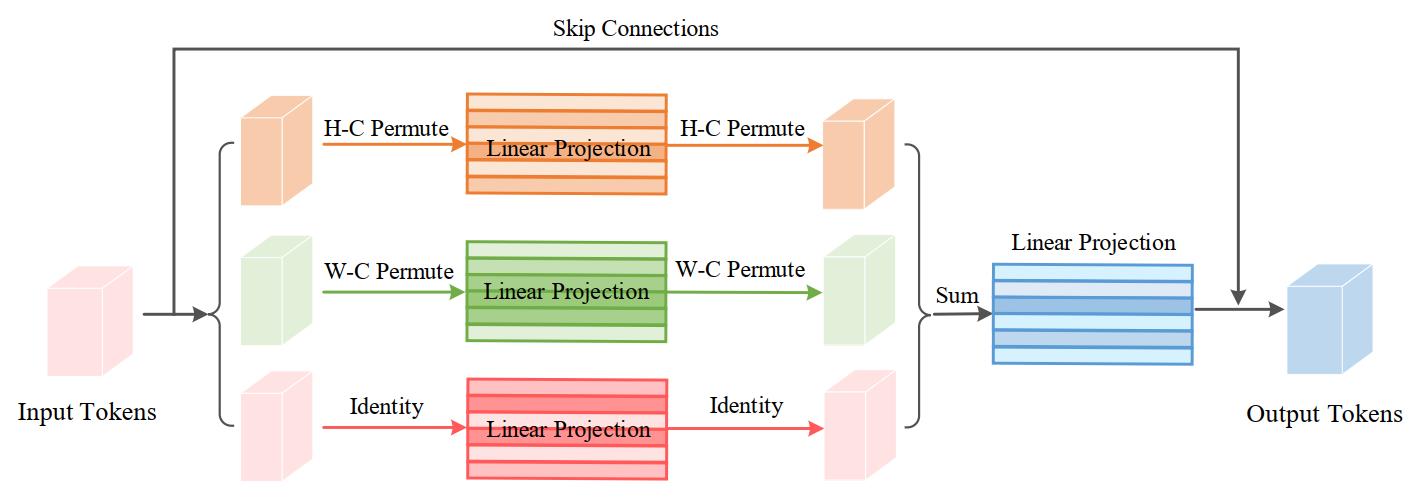
如上图所示，Permute-MLP包含三个分支，每个分支负责沿高度、宽度或通道维度对信息进行编码。其中通道信息的编码比较简单，只需要使用一个权重为${\mathbf{W}}_C\in {\mathbb{R}}^{C\times C}$的全连接层对输入进行$\mathbf{X}$进行线性投影即可，得到${\mathbf{X}}_C$，这就是上图最下面的分支。

下面介绍如何编码空间信息，其本质上是一个逐head的permute操作。假定隐层维度为384，输入图像为224x224的分辨率，为了沿着高度这个维度编码空间信息，首先需要对height和channel这两个维度进行调换（PyTorch中即为Permute操作）。那么具体如何做呢？对输入$\mathbf{X}\in {\mathbb{R}}^{H\times W\times C}$，首先沿着通道对其分成S组（每组为一个segment），即分为$\left[{\mathbf{X}}_{H_1},{\mathbf{X}}_{H_2},\cdots ,{\mathbf{X}}_{H_S}\right]$，每组包含$N$个通道，故有$C=N\ast S$。若patch size为$14\times 14$，$N$为16，则 X H i ∈ R H × W × N , ( i ∈ { 1 , ⋯   , S } ) \\mathbf{X}_{H_{i}} \\in \\mathbb{R}^{H \\times W \\times N},(i \\in\\{1, \\cdots, S\\}) XHi​​∈RH×W×N,(i∈{1,⋯,S})。接着，对每个segment ${\mathbf{X}}_{H_i}$进行height和channel的permute操作，产生的结果记为$\left[{\mathbf{X}}_{H_1}^{\top },{\mathbf{X}}_{H_2}^{\top },\cdots ,{\mathbf{X}}_{H_S}^{\top }\right]$，它们最终沿着通道维度concat到一起作为输出，接着这个输出送入一个参数为${\mathbf{W}}_H\in {\mathbb{R}}^{C\times C}$的全连接层中进行height信息的混合，然后再进行一次permute即可恢复维度，记这个输出为${\mathbf{X}}_H$，这就是上图的第一个分支。第二个分支是和第一个分支一样的操作不过针对于width这个维度，其输出为${\mathbf{X}}_W$。最后，这三个分支的输出加到一起然后通过一个全连接层得到最终的Permute-MLP的输出，可以用下式表示，其中$FC(\cdot )$表示一个参数为${\mathbf{W}}_P\in {\mathbb{R}}^{C\times C}$的全连接层。

$$\hat{\mathbf{X}}=\mathrm{F}\mathrm{C}\left({\mathbf{X}}_H+{\mathbf{X}}_W+{\mathbf{X}}_C\right)$$

作者也在论文中给出了Permute-MLP的PyTorch风格的伪代码，如下所示。

接着，作者发现上面这种相加融合三个分支的信息的方式采用的这种逐元素相加的操作效果不是很好，因此进一步提出了重校准不同分支重要性的加权融合方式，并顺势提出了Weighted Permute-MLP，和split attention操作类似，只不过split attention是对组卷积的一组tensor进行，这里是对${\mathbf{X}}_H,{\mathbf{X}}_W$和${\mathbf{X}}_C$进行的。这个过程并不复杂，我这里直接贴上作者的源码了，需要注意的是，下文所说的ViP默认均采用这种Weight Permute-MLP。

class WeightedPermuteMLP(nn.Module):
    def __init__(self, dim, segment_dim=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.segment_dim = segment_dim

        self.mlp_c = nn.Linear(dim, dim, bias=qkv_bias)
        self.mlp_h = nn.Linear(dim, dim, bias=qkv_bias)
        self.mlp_w = nn.Linear(dim, dim, bias=qkv_bias)

        self.reweight = Mlp(dim, dim // 4, dim *3)
        
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)



    def forward(self, x):
        B, H, W, C = x.shape

        S = C // self.segment_dim
        h = x.reshape(B, H, W, self.segment_dim, S).permute(0, 3, 2, 1, 4).reshape(B, self.segment_dim, W, H*S)
        h = self.mlp_h(h).reshape(B, self.segment_dim, W, H, S).permute以上是关于ViP解读：视觉MLP结构新作的主要内容，如果未能解决你的问题，请参考以下文章
 
 EANet解读
 EANet解读
 WGAN源码解读
 Halcon学习笔记-分类器mlp的解读
 开源新作！疯狂java讲义第四版
 谷歌最新提出无需卷积注意力 ，纯MLP构成的视觉架构！网友：MLP is All You Need ？...