Leetcode No.96 不同的二叉搜索树

Posted 2021-06-30 AI算法攻城狮

一、题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：
输入：n = 3
输出：5

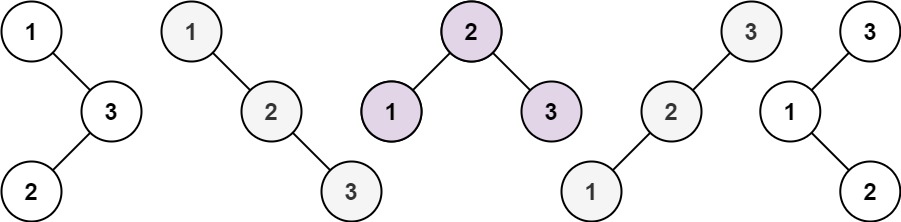
示例 2：
输入：n = 1
输出：1

提示：
1 <= n <= 19

二、解题思路

给定一个有序序列1⋯n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1⋯(i−1) 序列作为左子树，将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

在上述构建的过程中，由于根的值不同，因此我们能保证每棵二叉搜索树是唯一的。

由此可见，原问题可以分解成规模较小的两个子问题，且子问题的解可以复用。因此，我们可以想到使用动态规划来求解本题。

题目要求是计算不同二叉搜索树的个数。为此，我们可以定义两个函数：

G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。

F(i, n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。

可见，G(n)是我们求解需要的函数。

稍后我们将看到，G(n)可以从 F(i, n)得到，而 F(i, n)又会递归地依赖于 G(n)。

首先，根据上一节中的思路，不同的二叉搜索树的总数 G(n)，是对遍历所有 i(1≤i≤n) 的 F(i, n)之和。换言之：

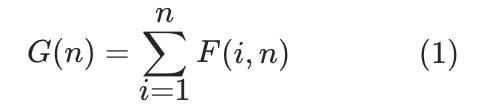
​ 对于边界情况，当序列长度为 1（只有根）或为 0（空树）时，只有一种情况，即：
G(0)=1,G(1)=1

给定序列 1⋯n，我们选择数字 i 作为根，则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积，对于笛卡尔积中的每个元素，加上根节点之后形成完整的二叉搜索树，如下图所示：

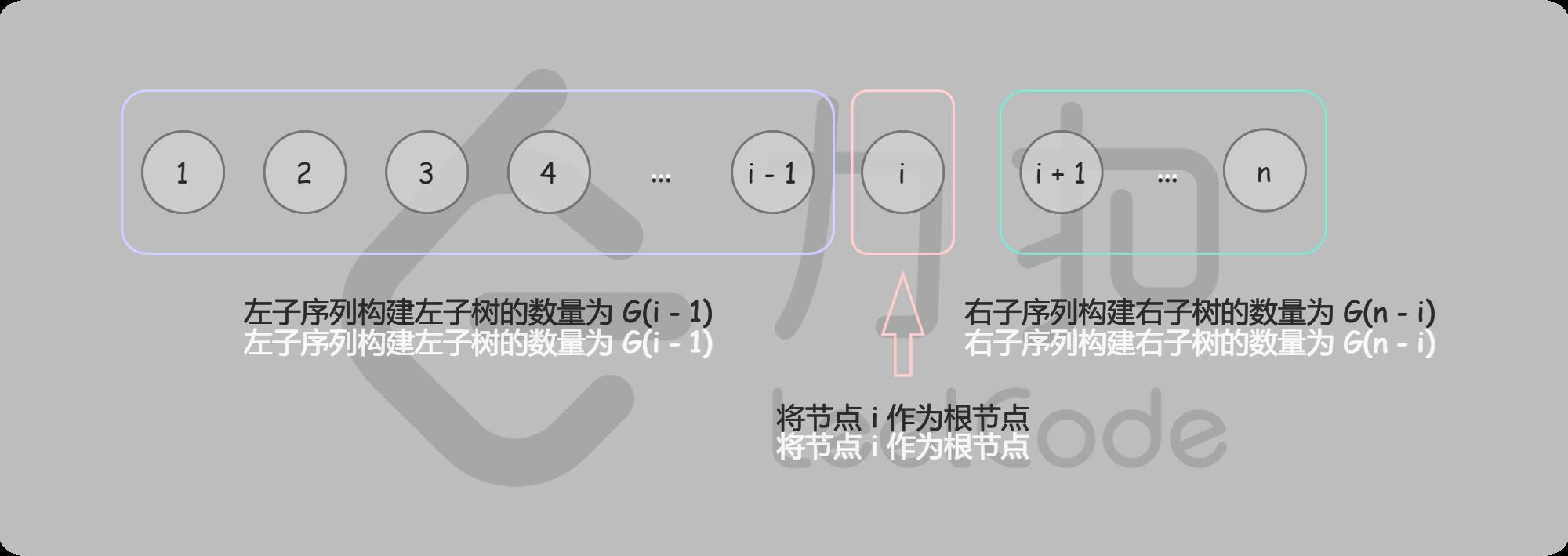
举例而言，创建以 3 为根、长度为 7 的不同二叉搜索树，整个序列是[1,2,3,4,5,6,7]，我们需要从左子序列[1,2] 构建左子树，从右子序列[4,5,6,7] 构建右子树，然后将它们组合（即笛卡尔积）。

对于这个例子，不同二叉搜索树的个数为 F(3,7)。我们将 [1,2] 构建不同左子树的数量表示为 G(2), 从 [4,5,6,7] 构建不同右子树的数量表示为 G(4)，注意到 G(n) 和序列的内容无关，只和序列的长度有关。于是，F(3,7)=G(2)⋅G(4)。 因此，我们可以得到以下公式：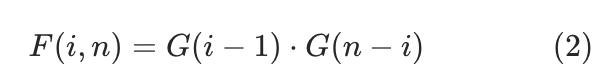

将公式 (1)，(2) 结合，可以得到G(n) 的递归表达式：

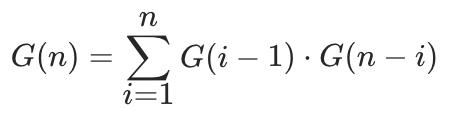
​   至此，我们从小到大计算 G函数即可，因为 G(n) 的值依赖于 G(0)⋯G(n−1)。

三、代码

public class Solution {
    public int numTrees(int n) {
        int[] g= new int[n+1];
        g[0]=1;
        g[1]=1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                g[i]+=g[j]*g[i-j];
            }
        }
        return g[n];
    }
}

四、复杂度分析

时间复杂度 : O(n^2)，其中 n 表示二叉搜索树的节点个数。G(n) 函数一共有 n个值需要求解，每次求解需要 O(n)的时间复杂度，因此总时间复杂度为 O(n^2)。

空间复杂度 : O(n)。我们需要O(n) 的空间存储 G 数组。