机器学习- 吴恩达Andrew Ng Week8 知识总结 Dimensionality Reduction

Posted 2021-06-30 架构师易筋

Coursera课程地址

因为Coursera的课程还有考试和论坛，后续的笔记是基于Coursera
https://www.coursera.org/learn/machine-learning/home/welcome

降维Dimensionality Reduction

1 动机一：数据压缩 Motivation I: Data Compression

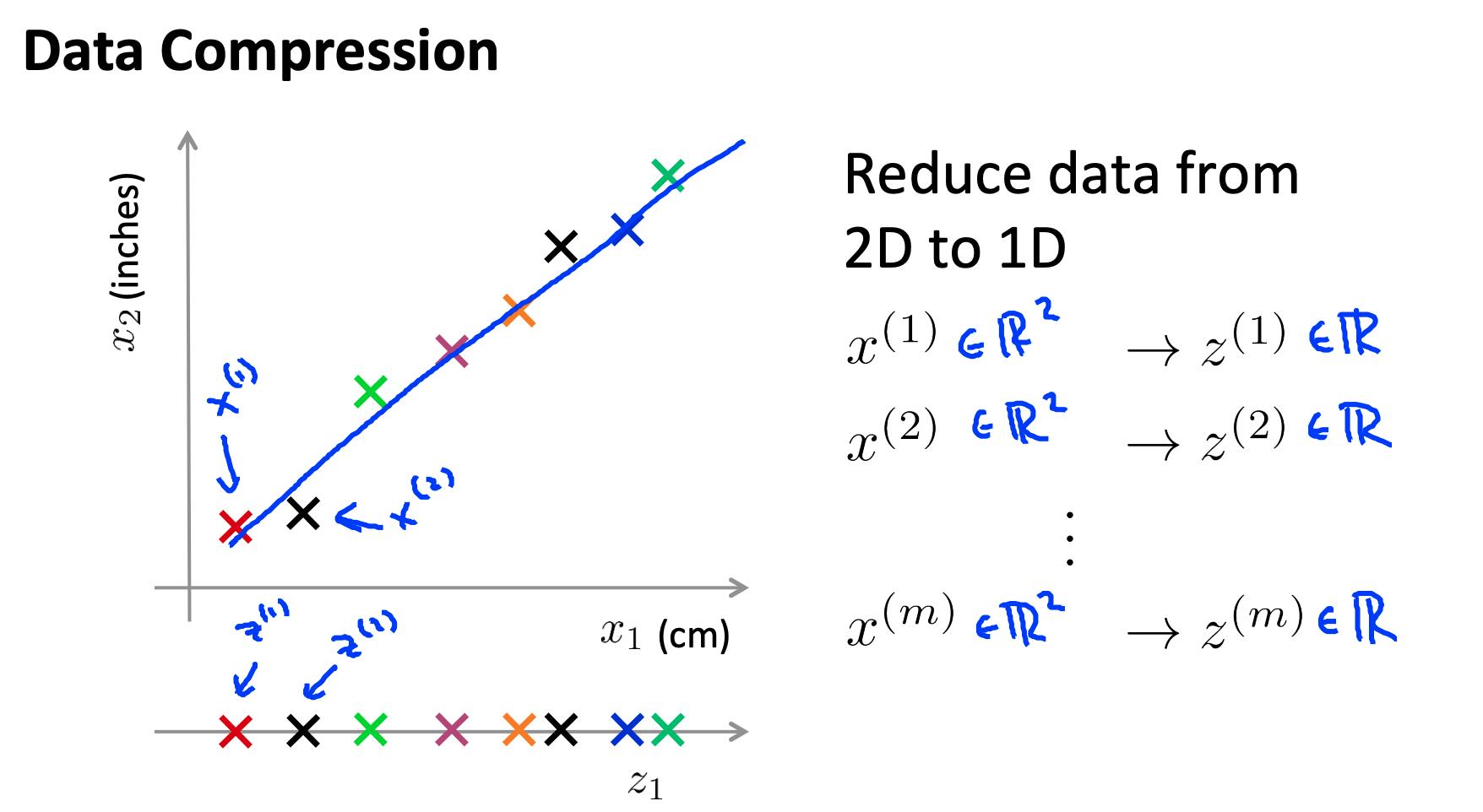
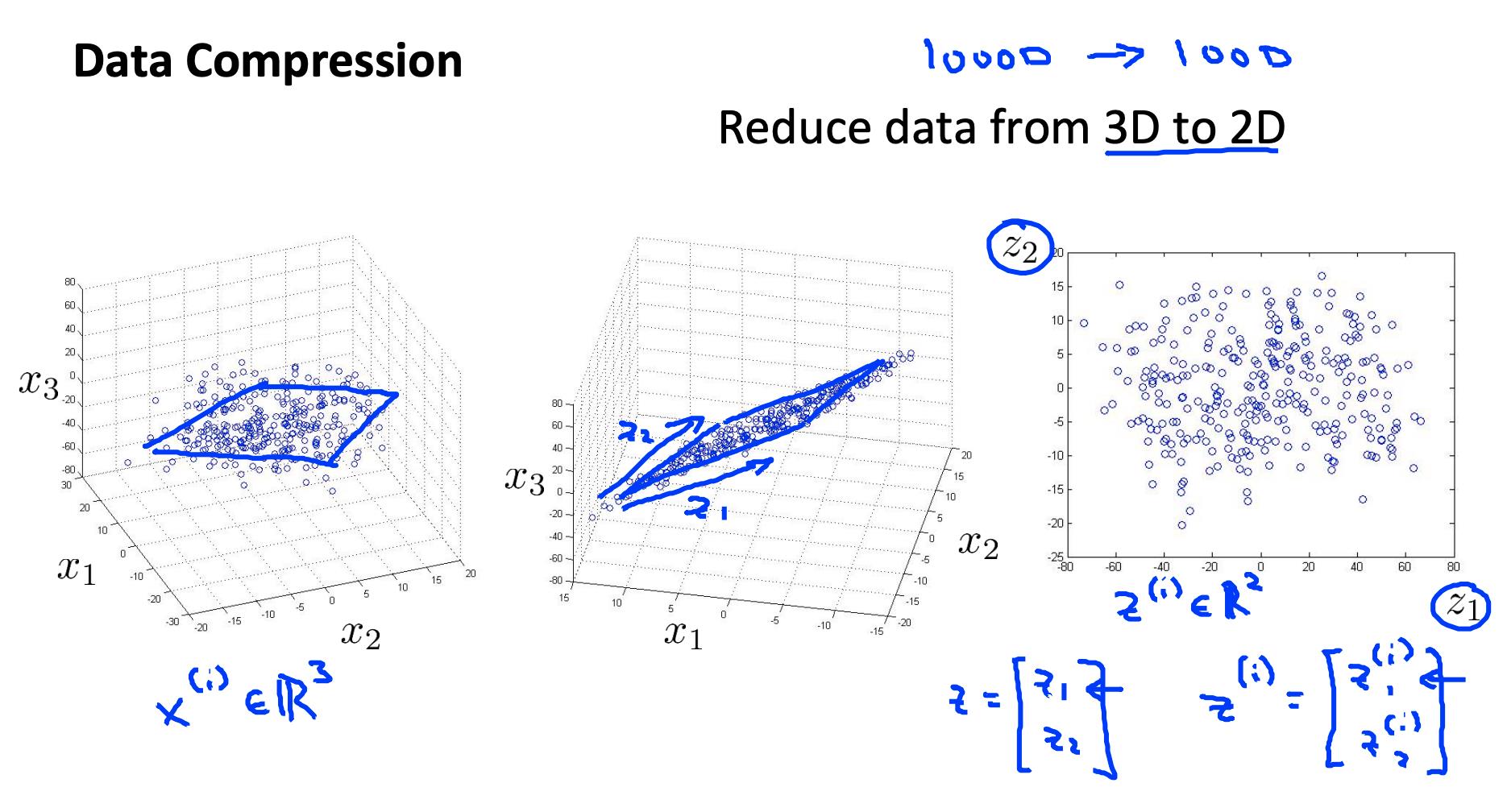
• 如果我们有很多冗余数据，我们可能希望减少特征的维度。
• 为此，我们找到两个高度相关的特征，绘制它们，并创建一条新线，似乎准确地描述了这两个特征。我们将所有新功能放在这一行中。

进行降维将减少我们必须存储在计算机内存中的总数据，并加快我们的学习算法。

注意：在降维中，我们正在减少我们的特征而不是我们的示例数量。我们的变量 m 将保持不变；n，每个示例的特征数X(1)至X(m)携带，会减少。

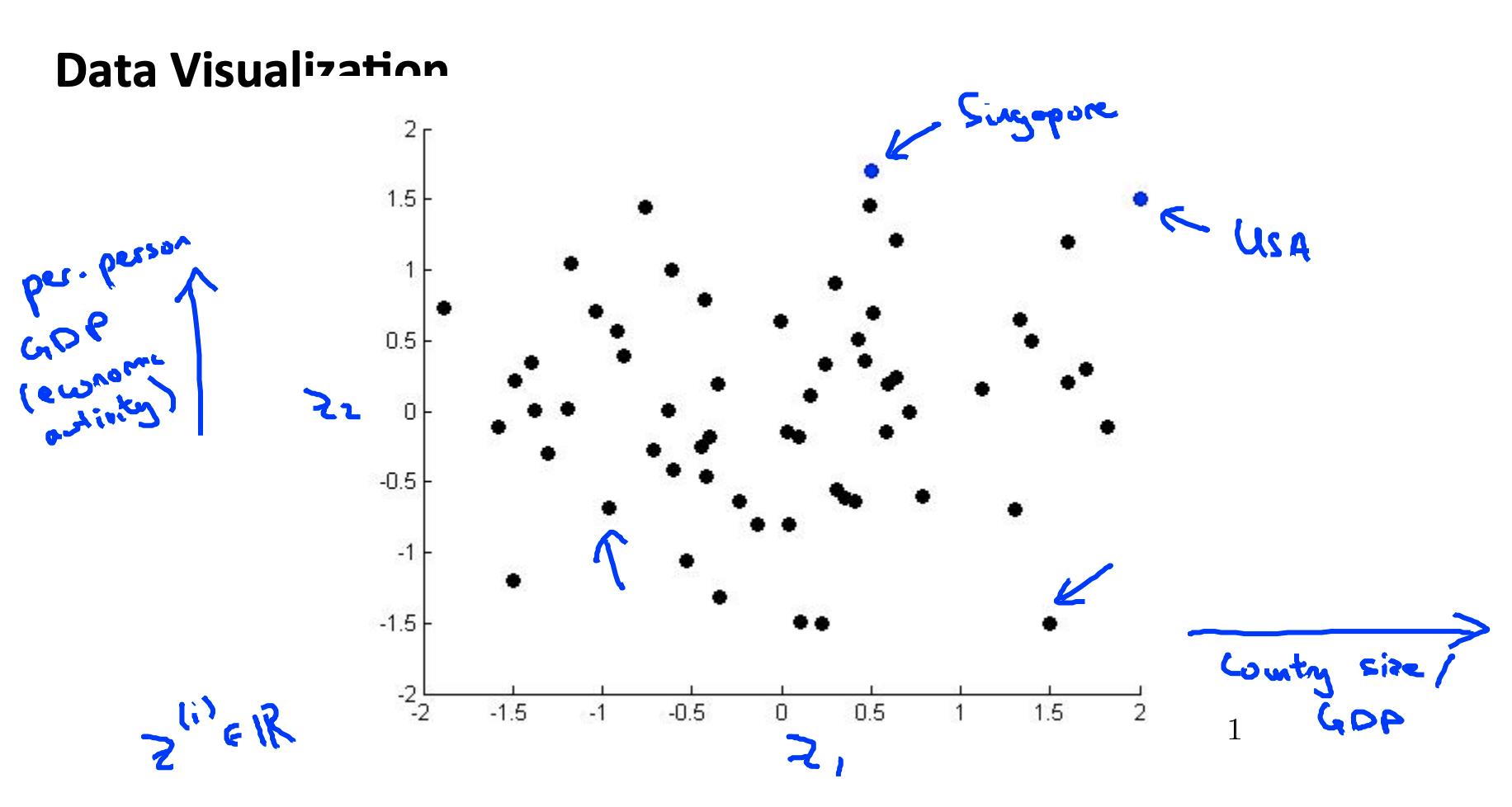
2 动机二：可视化 Motivation II: Data Visualization

可视化超过三个维度的数据并不容易。我们可以将数据的维度减少到 3 或更少以绘制它。

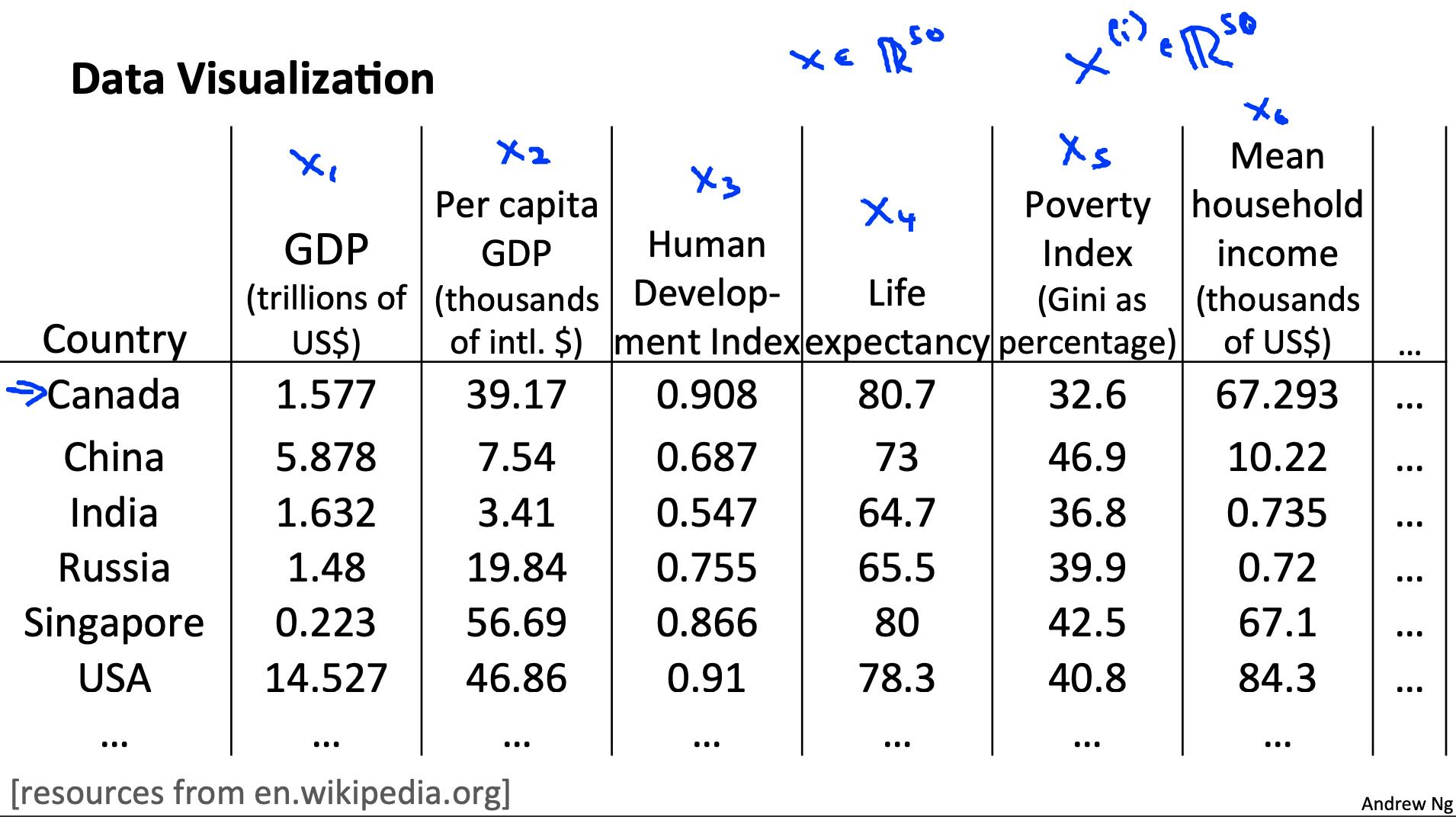
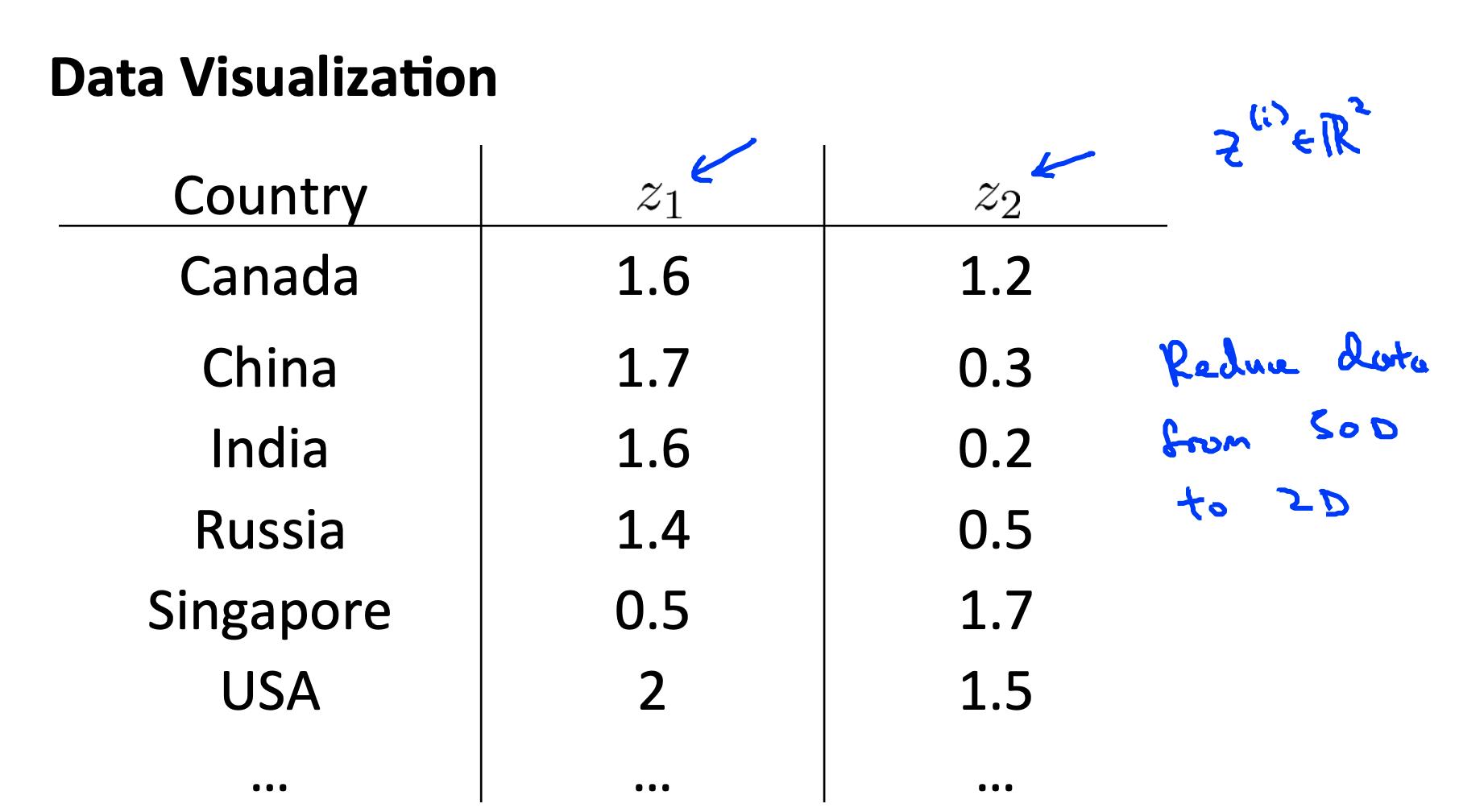
我们需要寻找新的功能， z1, z2z （也许 z3 ) 可以有效地总结所有其他功能。

示例：与一个国家的经济系统相关的数百个特征可能都被组合成一个特征，您称之为“经济活动”。

3. 主成分分析问题公式化 Principal Component Analysis Problem Formulation

最流行的降维算法是主成分分析（PCA）

3.1 问题表述

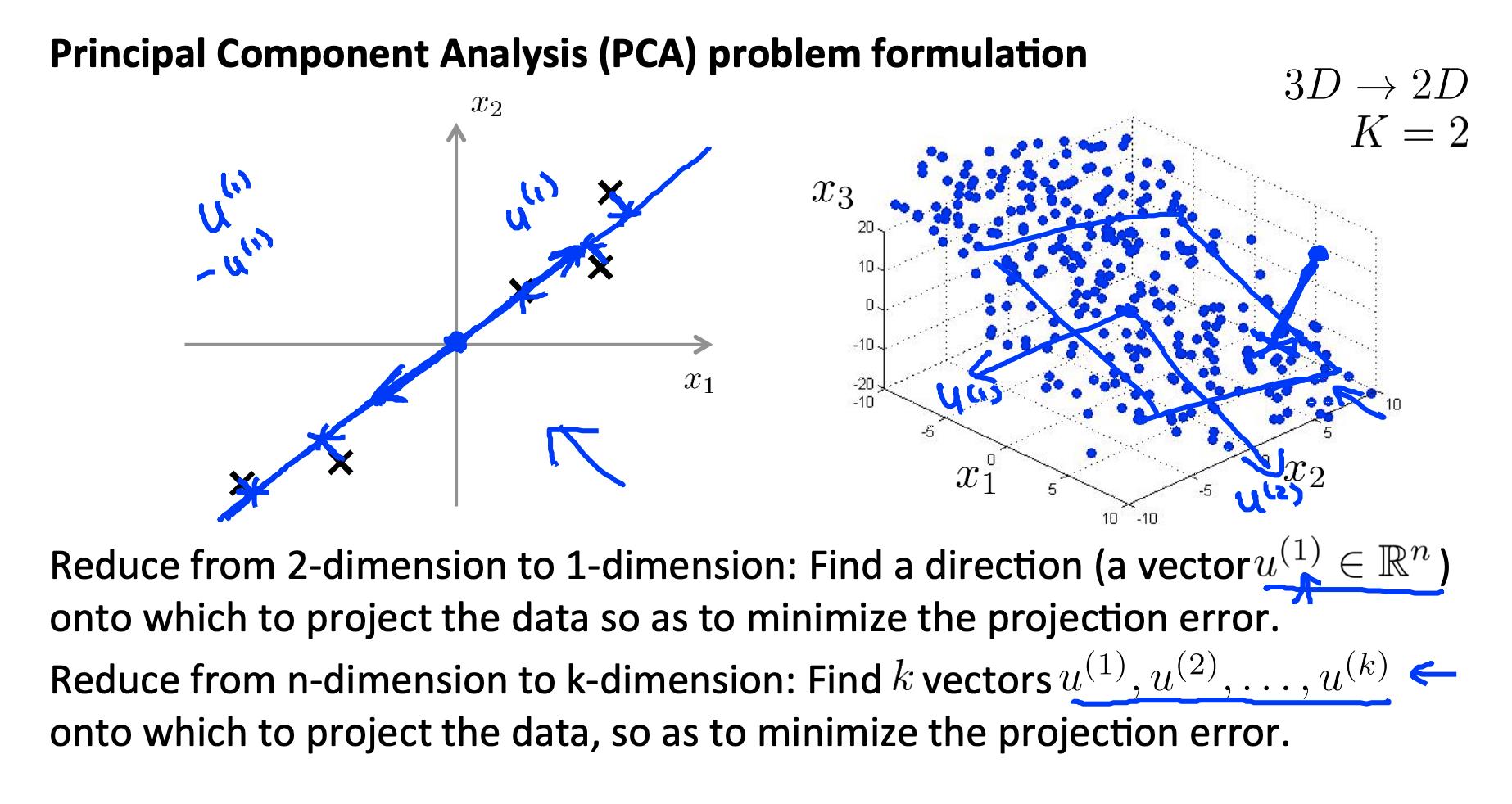
鉴于两个特点， X1 和 X2，我们想找到一行同时有效地描述这两个特征的行。然后我们将我们的旧功能映射到这条新线上以获得一个新的单一功能。

同样可以用三个特征来完成，我们将它们映射到一个平面。

PCA的目标是减少每个特征到投影线的所有距离的平均值。这是投影误差。

从 2d 减少到 1d：找到一个方向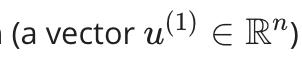

将数据投影到其上以最小化投影误差。

更一般的情况如下：
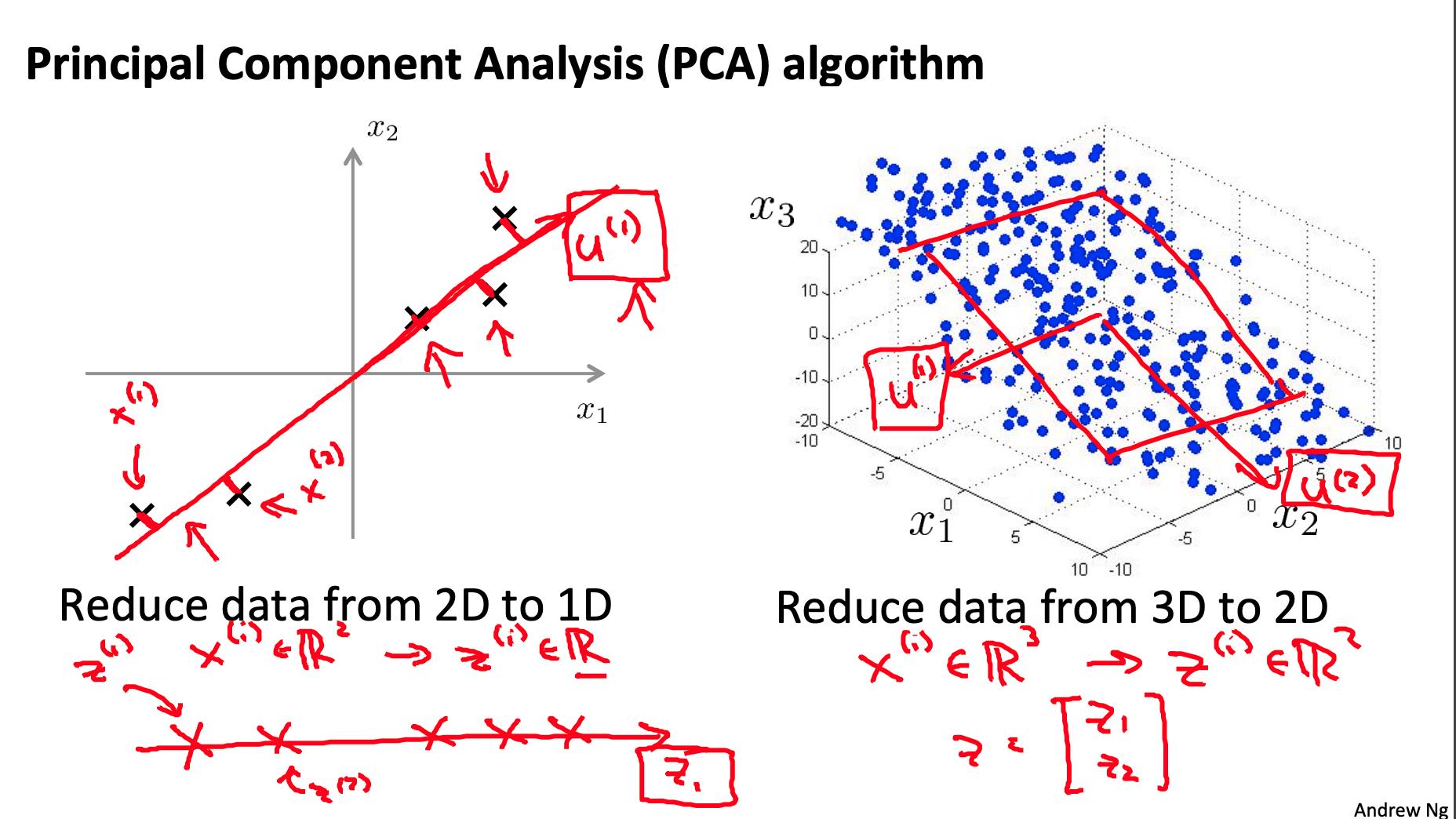
从 n 维减少到 k 维：找到 k 个向量 u(1), u(2), … u(k)将数据投影到其上以最小化投影误差。

如果我们要从 3d 转换为 2d，我们会将数据投影到两个方向（一个平面）上，因此 k 将为 2。

3.2 PCA 不是线性回归

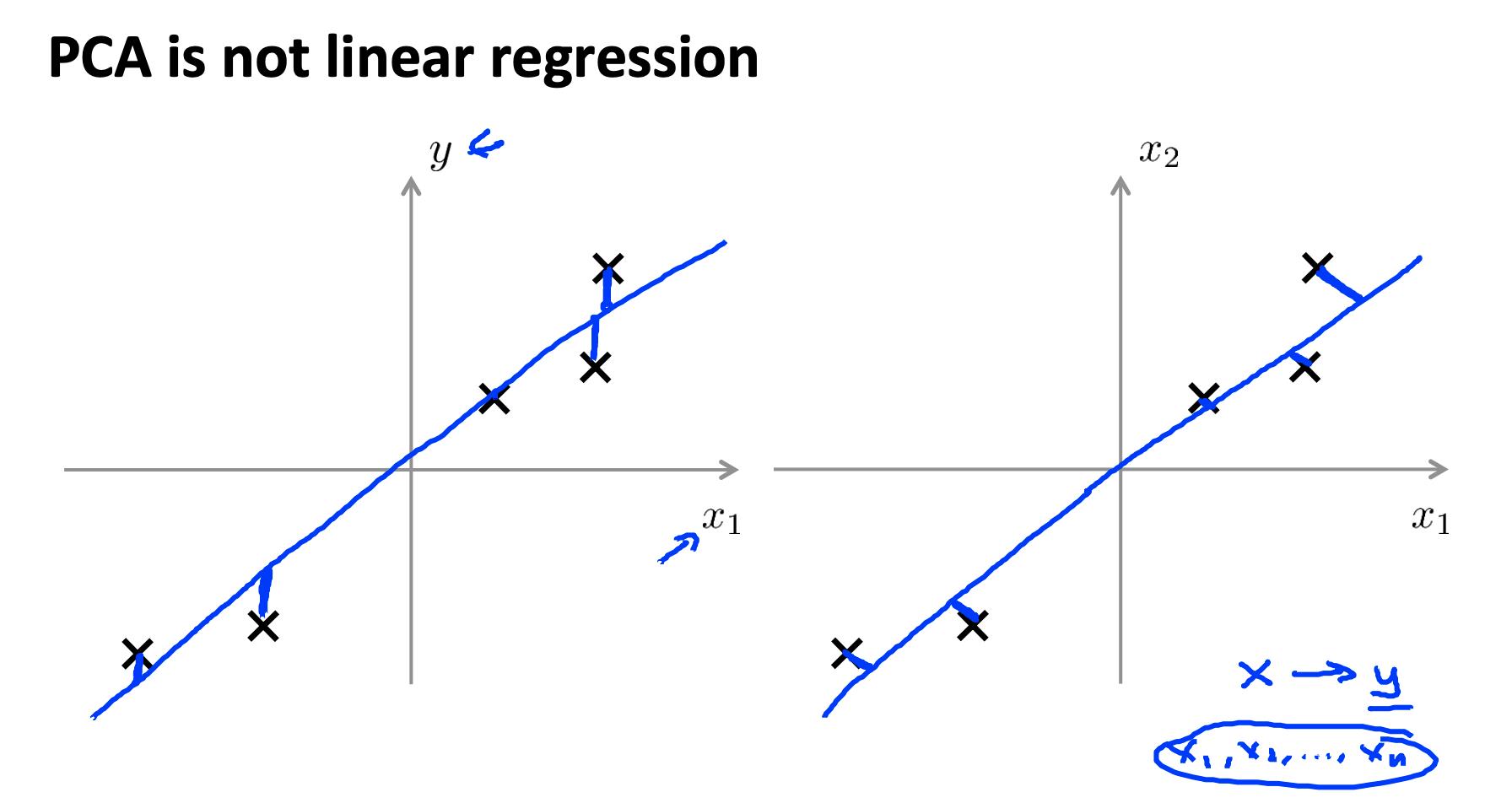
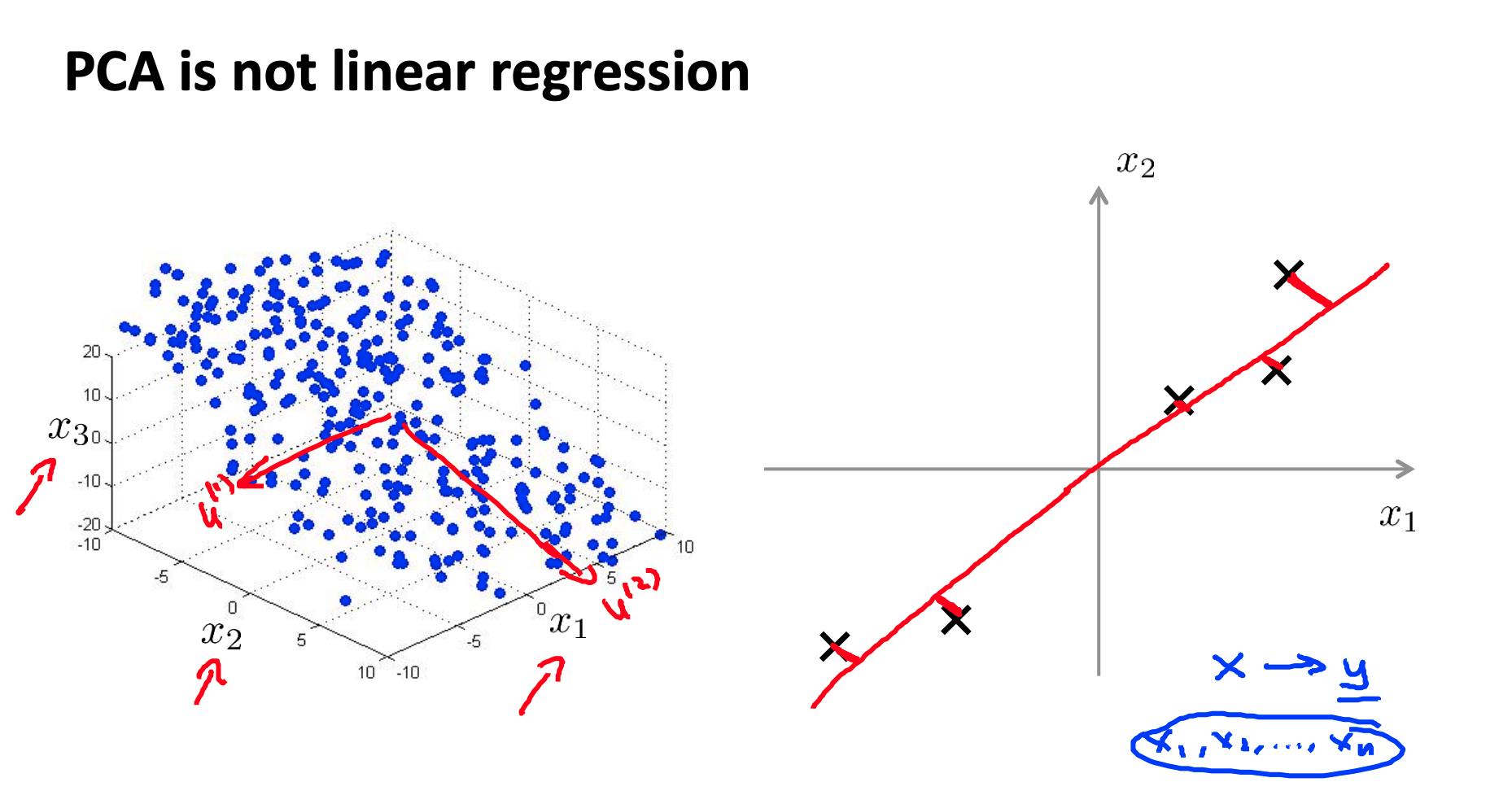
• 在线性回归中，我们最小化从每个点到我们的预测线的平方误差。这些是垂直距离。
• 在 PCA 中，我们最小化到数据点的最短距离或最短正交距离。

更一般地，在线性回归中，我们采用 x 中的所有示例并应用 Θ 中的参数来预测 y。

在 PCA 中，我们采用了许多功能 X1 ,X2 ,…,Xn ，并在其中找到最接近的公共数据集。我们不会尝试预测任何结果，也不会对特征应用任何 theta 权重。

4. 主成分分析算法 Principal Component Analysis algorithm

在我们可以应用 PCA 之前，我们必须执行一个数据预处理步骤：

数据预处理

• 给定训练集: x(1), x(2), …, x(m).

• 预处理（特征缩放/均值归一化）：
  

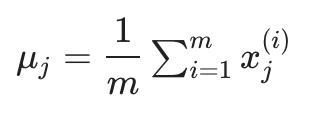
• 更换每个

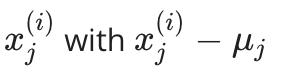
• 如果不同尺度上的不同特征（例如， X1 = 房子的大小， X2 = 卧室数），缩放特征以具有可比较的值范围。

上面，我们首先从原始特征中减去每个特征的均值。然后我们缩放所有特征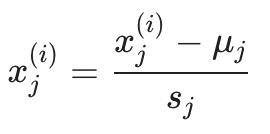

我们可以具体定义从 2d 到 1d 数据的含义如下：

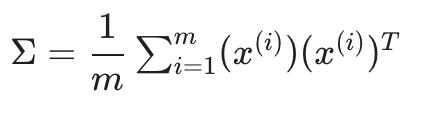
z 值都是实数，是我们的特征在u(1).

所以，PCA 有两个任务：找出u(1), …, u(k), 并且还要找到 z1, z2, …, zm.
以下过程的数学证明很复杂，超出了本课程的范围。

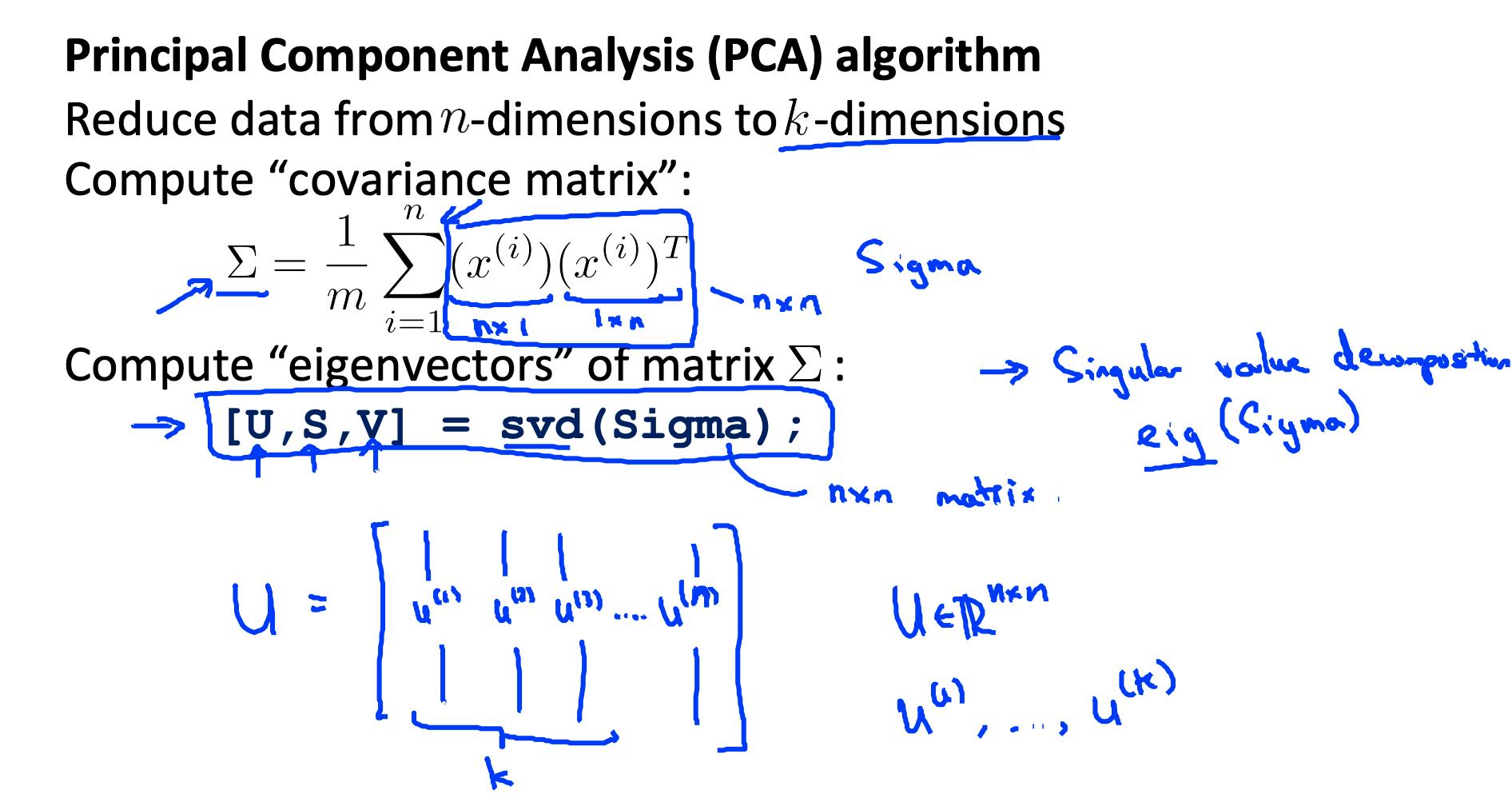
4.1 计算“协方差矩阵”

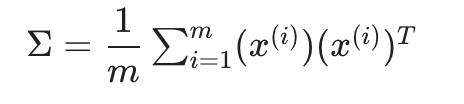
这可以在 Octave 中向量化为：

Sigma = (1/m) * X' * X;

我们用大写的 sigma 表示协方差矩阵（这恰好是求和的相同符号，令人困惑——它们代表完全不同的东西）。
注意x(i), 是一个n x 1向量, (x(i))T 是一个 1xn向量，X 是 mxn矩阵（按行存储的示例）。它们的乘积将是一个 n×n 矩阵，它们是 Σ 的维度。

4.2 计算协方差矩阵 Σ 的“特征向量”

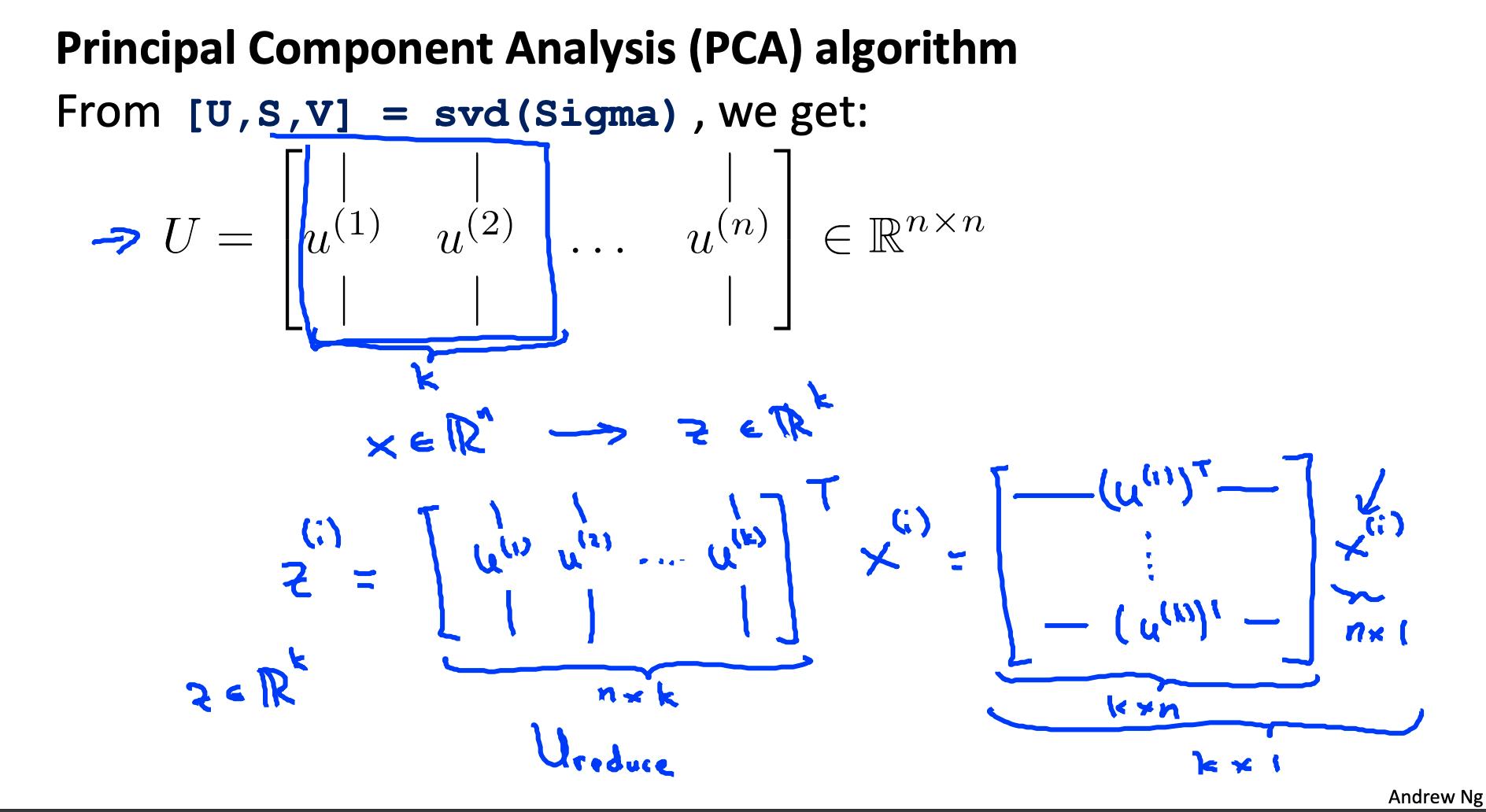
[U,S,V] = svd(Sigma);

svd() 是“奇异值分解”，一个内置的 Octave 函数。

4.3 取U矩阵的前k列并计算z

我们将 U 的前 k 列分配给名为“Ureduce”的变量。这将是一个 n×k 矩阵。我们用以下方法计算 z：


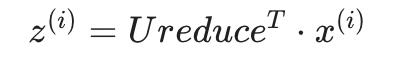
总结一下，整个octave算法大致是：

Sigma = (1/m) * X' * X; % compute the covariance matrix
[U,S,V] = svd(Sigma);   % compute our projected directions
Ureduce = U(:,1:k);     % take the first k directions
Z = X * Ureduce;        % compute the projected data points

5. 从压缩到重建 Reconstruction from compressed representation

如果我们使用 PCA 来压缩我们的数据，我们如何解压缩我们的数据，或者回到我们原来的特征数量？

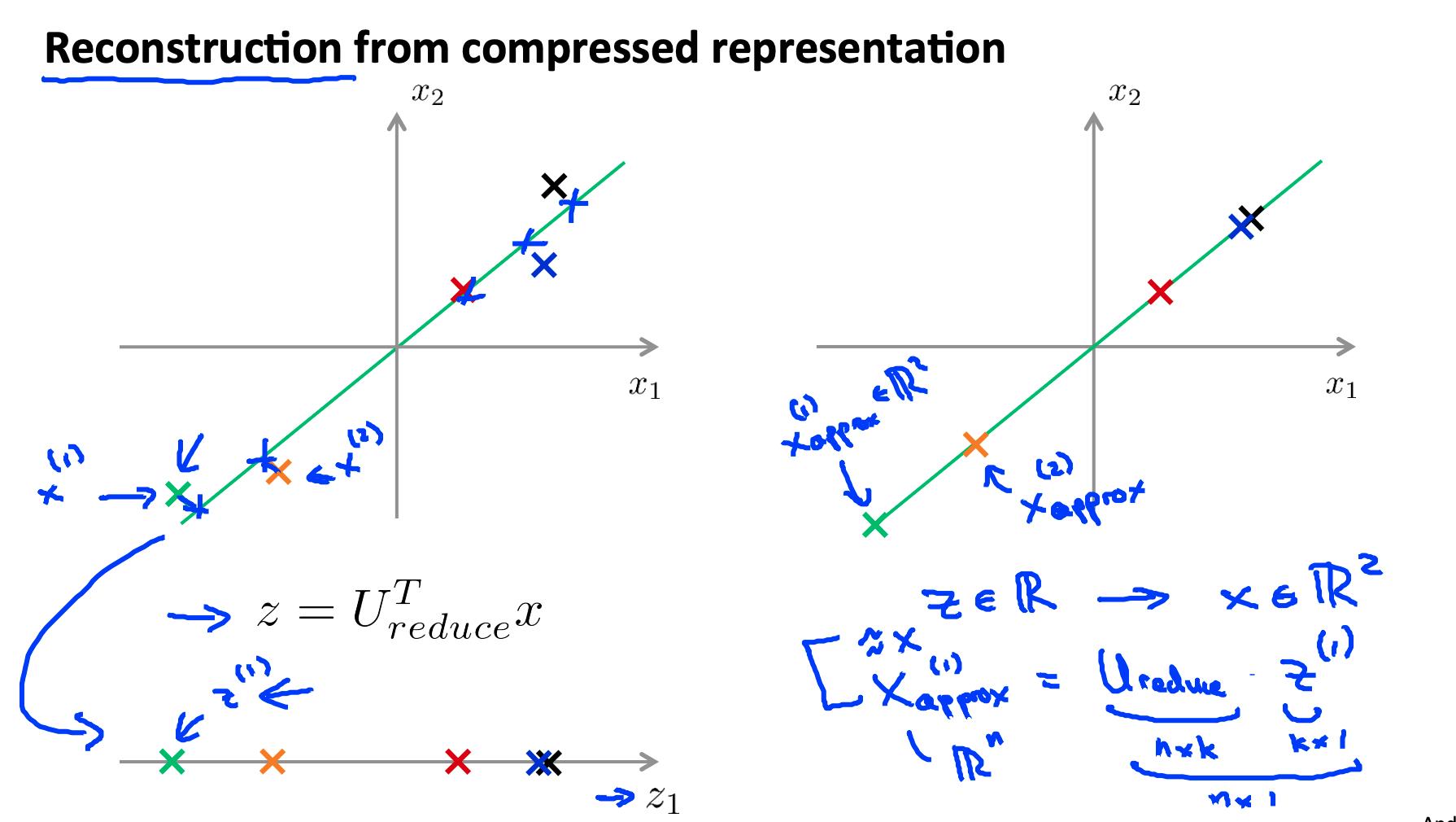
为了从一维回到二维，我们这样做 z∈R→x∈R^2 .

我们可以用等式来做到这一点：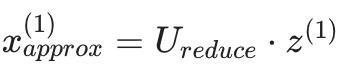

请注意，我们只能获得原始数据的近似值。

注意：事实证明，U 矩阵具有特殊的性质，即它是Unitary Matrix。Unitary Matrix的特殊性质之一是：U^(-1) = U*, 其中“*”表示“共轭转置”。

由于我们在这里处理实数，这相当于：

U^(-1) = U^T所以我们可以计算逆并使用它，但这会浪费能量和计算周期。

6. 选择主成分的数量 Choosing the number of principal components

我们如何选择k，也称为主成分数？回想一下，k 是我们要缩减到的维度。

选择 k 的一种方法是使用以下公式：

• 给定平均平方投影误差：

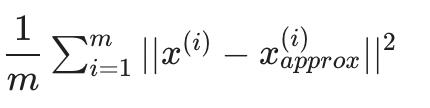
• 还给出了数据的总变化:

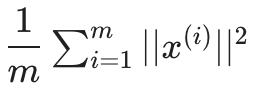
• 选择 k 作为最小值，使得：

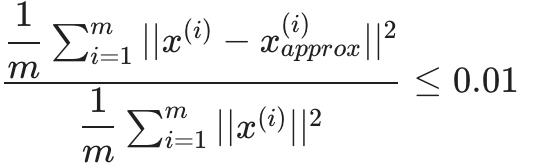
换句话说，平方投影误差除以总变异应该小于百分之一，这样才能保留 99% 的方差。

选择k的算法

1. 尝试使用 k=1,2 的 PCA，…
2. 计算 U(reduce), z, x.
3. 检查上面给出的公式，保留 99% 的方差。如果不是，则转到第一步并增加 k。

这个过程实际上会非常低效。在 Octave 中，我们将调用 svd：

[U,S,V] = svd(Sigma)

这给了我们一个矩阵 S。我们实际上可以使用 S 矩阵检查 99% 的保留方差，如下所示：

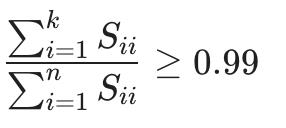
7. 应用PCA的建议 Advice for Applying PCA

PCA 最常见的用途是加速监督学习。

给定具有大量特征的训练集 (e.g. x(1), …, x(m) ∈ R(10000)),
我们可以使用 PCA 来减少训练集的每个示例中的特征数量(e.g. x(1), …, x(m) ∈ R(10000))

请注意，我们应该将 PCA 减少定义为从x(i) 到 z(i) 仅在训练集上，而不是在交叉验证或测试集上。在训练集上定义后，您可以将映射 z(i) 应用于交叉验证和测试集。

应用

• 压缩

减少数据空间

加速算法

• 数据可视化

选择 k = 2 或 k = 3

PC A 的错误使用：试图防止过度拟合。我们可能认为使用 PCA 减少特征将是解决过度拟合的有效方法。它可能有效，但不推荐，因为它不考虑我们的结果 y 的值。仅使用正则化至少同样有效。

不要假设你需要做 PCA。首先尝试没有 PCA 的完整机器学习算法。如果您发现需要，请使用 PCA。

参考

https://www.coursera.org/learn/machine-learning/supplement/SCJi4/lecture-slides

https://www.coursera.org/learn/machine-learning/resources/kGWsY