Codeforces Round#728 div.1+div.2题解

Posted 2021-06-30 欣君

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Codeforces Round#728 div.1+div.2题解相关的知识，希望对你有一定的参考价值。

div.2 视频讲解：BV19f4y1t7En
div.1 视频讲解：TBD

div.2-A. Pretty Permutations

题目大意

有 $n$ 只猫排成一排，标记为 $1$ 到 $n$ ，第 $i$ 只猫位于位置 $i$ 。他们厌倦了整天在同一个地方打转，所以他们想重新安排自己，这样猫就不会像以前一样在同一个地方了。他们也很懒惰，所以他们想尽量减少他们移动的总距离。帮助他们决定在重新排序后每个位置应该放什么猫。

例如，如果有 $3$ 只猫，这是一个有效的重新排序： $[3, 1, 2]$ 。没有猫在原来的位置。猫移动的总距离为 $1 + 1 + 2 = 4$ ，因为猫 $1$ 向右移动一位，猫 $2$ 向右移动一位，而猫 $3$ 向左移动两位。

题解

贪心可得，相邻交换最优。
若 $n$ 为偶数，则相邻奇偶位交换。
若 $n$ 为奇数，则有三只猫轮换，剩余相邻奇偶位交换。

参考代码

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
 
int main()
{
	int T,n,i;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n);
		if(n%2)
		{
			printf("3 1 2");
			for(i=4;i<=n;i+=2)
				printf(" %d %d",i+1,i);
				puts("");
		}
		else
		{
			for(i=1;i<=n;i+=2)
				printf("%d %d ",i+1,i);
			puts("");
		}
	}
}

div.2-B. Pleasant Pairs

题目大意

给定包含 $\\leq n \\leq 2 \\cdot 10^5)$ 个不同元素的数组 $a_i(1 \\leq a_i \\leq 2 \\cdot n)$ ，求满足以下条件的 $(i, j)$ 对：

$i < j$ ；
$a_i*a_j=i+j$ ；

题解

对于每个 $i$ ，暴力枚举所有 $a_i$ 的倍数然后判断即可，注意 $\\neq j$ 。
复杂度可以用调和级数证明为 $\\cdot log(n))$ 。

参考代码

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

const int MAXN=100100;
int a[MAXN];
map<int,int> mp;

int main()
{
	int T,n,i,j,k,ans;
	scanf("%d",&T);
	while(T--)
	{
		mp.clear();
		scanf("%d",&n);
		for(i=1;i<=n;i++)
		{
			scanf("%d",&a[i]);
			mp[a[i]]=i;
		}
		ans=0;
		for(i=1;i<=n;i++)
		{
			for(k=a[i];k<=2*n;k+=a[i])
			{
				j=mp[k/a[i]];
				if(j&&j^i)
					ans+=(k==i+j);
			}
		}
		printf("%d\\n",ans/2);
	}
}

div.2-C/div.2-A. Great Graphs

题目大意

已知有一张包含 $\\leq n \\leq 10^5)$ 个节点的有向图。有向图上每条边有边权值，边权值可能为正也可能为负，不存在负环。
已知节点 $1$ 到每个节点的最短距离 $d_i$ ，求满足条件的图中，边权值总和最小为多少。

题解

边权值总和最小时，必然只有一条正边，指向最远的节点。
同时，每个节点 $i$ 会有负边指向其他更近的节点 $j$ ，权值为 $d_j-d_i(d_j < d_i)$ 。
实现时，对所有距离排序后用前缀和处理即可。

参考代码

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

const int MAXN=100100;
ll d[MAXN],sum[MAXN];

int main()
{
	int T,i,n;
	ll mx,ans;
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&n);
		for(i=1;i<=n;i++)
			scanf("%lld",&d[i]);
		sort(d+1,d+n+1);
		for(i=1;i<=n;i++)
			sum[i]=sum[i-1]+d[i];
		ans=d[n];
		for(i=1;i<=n;i++)
			ans+=sum[i-1]-sum[0]-(i-1)*d[i];
		printf("%lld\\n",ans);
	}
}

div.2-D/div.1-C. Tree Array

题目大意

给定一个包含 $\\leq n \\leq 200)$ 个节点的树，对树上的节点进行 $1$ 到 $n$ 编号。
一开始随机选择一个节点，标记为 $1$ 。
之后每次随机选择一个与已被标记的节点相邻的未标记节点，进行标记。直到所有节点都被标记完。
设 $a_i$ 为节点 $i$ 被标记的编号。求数列 $a_i$ 的逆序数对数量的期望。

题解

考虑一对逆序数对 $i,j)(i < j,a_i>a_j)$ 出现的概率 $P_{i,j}$ ，则易得总期望为
$E=\\sum_{i=1}^n{\\sum_{j=i+1}^n{P_{i,j}}}$
以下图为例，假设 $i = A, j = B, A < B$ ，如果希望使得 $a_A>a_B$ ，那么必须先访问到 $B$ 再访问 $A$ 。

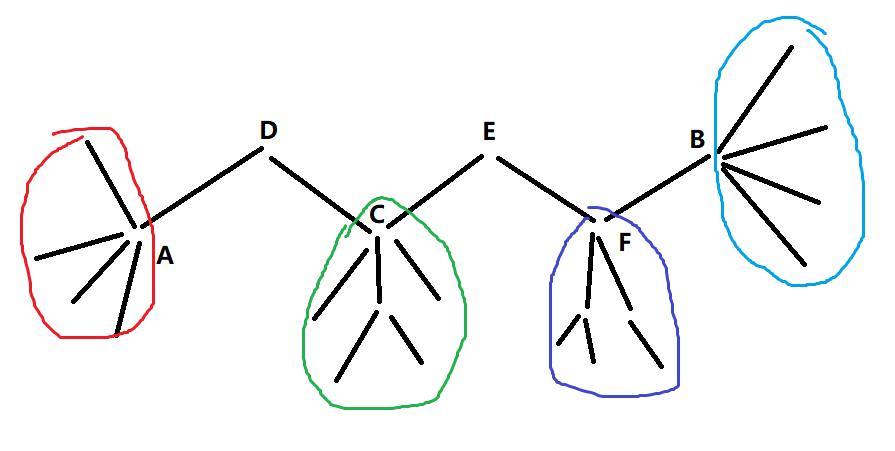
有以下三种情况：