快速排序(递归和非递归)及其优化

Posted 2021-06-30 两片空白

文章目录

• 一.定义
• 二.实现
• 三.优化
• 四.非递归

一.定义

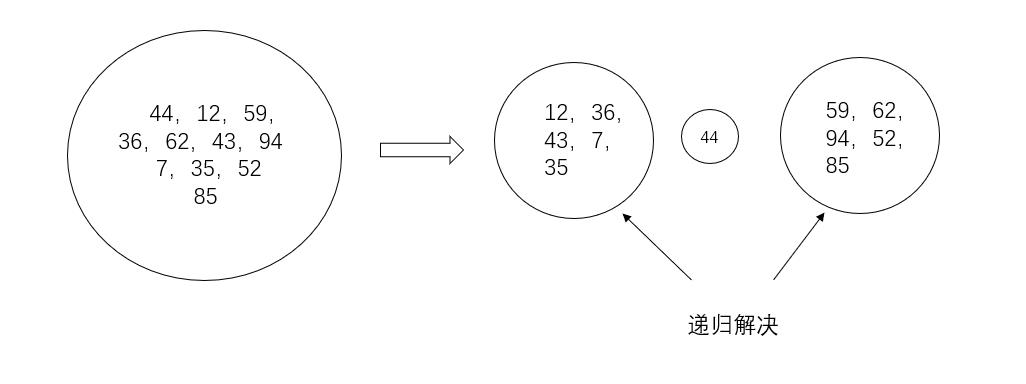
快速排序也是交换排序的一种，其原理是：将未排序元素中的一个作为基准的主元(Pivot)将未排序序列分为两个子序列，其中一个子序列均小于主元，而另一子序列均大于主元，然后递归的对这两个子序列用同样的方法进行排序。本质上，快速排序使用分治法，将问题规模减小，然后进行分别处理。
一般我们选用左边第一个元素作为主元。

二.实现

1. 挖坑法

可见我之前博客快排挖坑法

2. 前后指针法
   
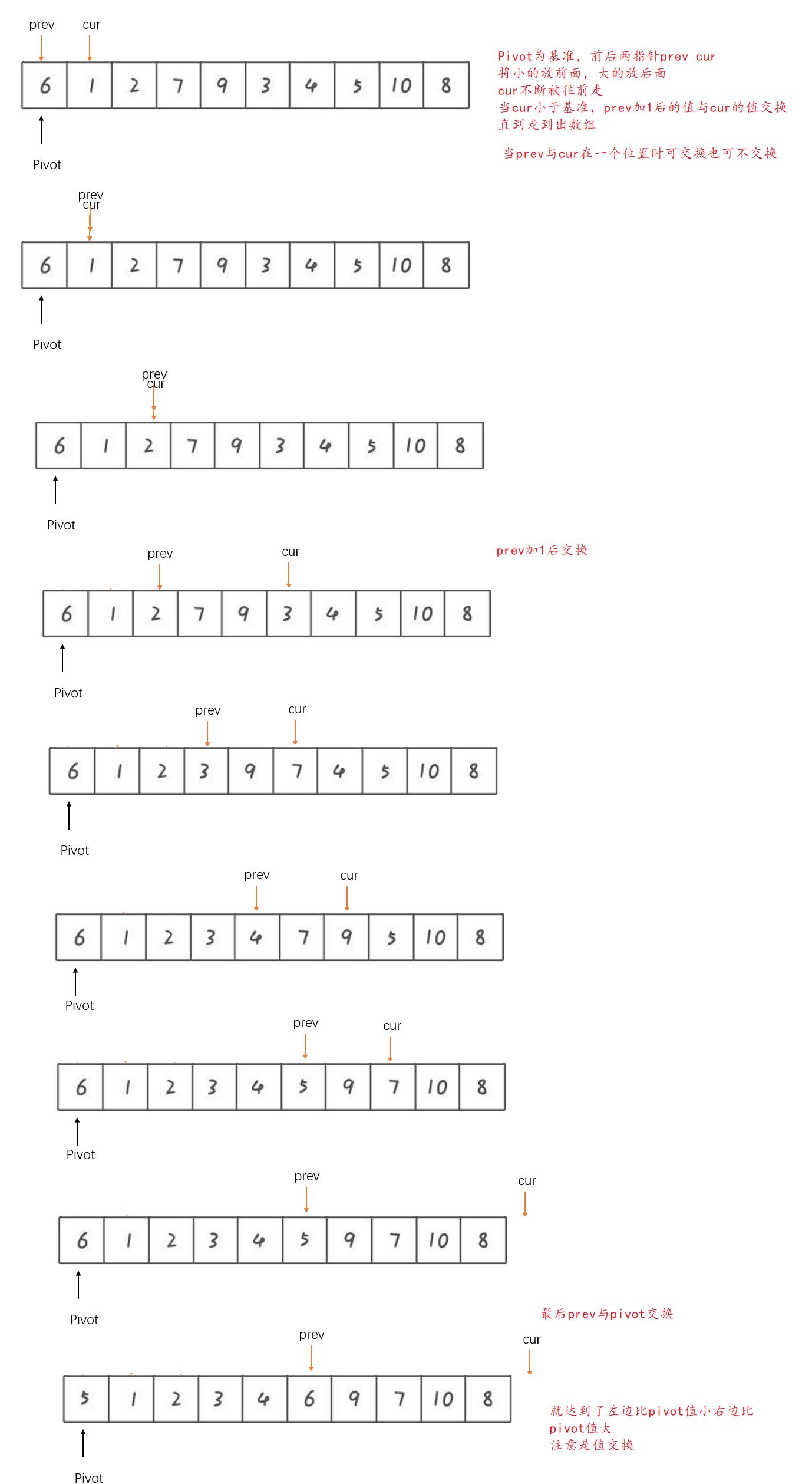
   代码如下：

void Swap(int *px, int *py){
	int temp = *px;
	*px = *py;
	*py = temp;
}
//前后指针法
int GetPostion2(int *a,int left,int right){
	int key = left;
	int prev = left;
	int cur = left + 1;
	while (cur <= right){
		if (a[cur] < a[prev] && ++prev != cur){//相等时prev加1不交换
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[prev], &a[key]);//prev不用加1了
	return prev;
}

三.优化

快速排序时间复杂度分析略微复杂，最好情况下，每次划分都将原序列分成两个基本等长的子序列，随着递归层次的加深，子序列数量翻倍，但是每个递归层次上比较总数都是O(N)次，而递归深度为logN,由此可见快排最好时间复杂度为O(NlogN)。但是在最坏的情况下(有序)，每次两边子序列，一边近似于1，一边近似于N-1，这样递归就不像一个数结构，而像一个链结构，时间复杂度为O(N^2)。
为了避免着用最坏结果，选取主元时需要一定的技巧。假设A为要排序序列，选主元时将最左边，最右边和中将元素值中间的这个作为主元，这样递归就可以最好的接近树结构，但是主元选中间位置，不好进行比较交换。于是我们将中间数与最左边数交换，依然让最左边做主元位置。
还有一个问题，由于快排一般是用递归实现，在时间是和空间上都有一定的消耗，如果带排序序列规模较小，递归副作用就会体现出来，效果还不如插入排序。为了解决这一问题，在递归过程中选择某一阈值，当小于这一阈值时不进行递归，直接进行插入排序。

代码实现：

//三数找中间数快排
//找中间这个数，和最左最右数得到中间数
//防止最坏的结果有序
int Getmid(int *a, int left, int right){
	int mid = left + (right - left) / 2;
	if (a[left] < a[mid]){
		if (a[right] < a[left]){
			return left;
		}
		else if (a[right]>a[mid]){
			return mid;
		}
		else{
			return right;
		}
	}
	else{
		if (a[right] < a[mid]){
			return mid;
		}
		else if (a[right]>a[left]){
			return left;
		}
		else{
			return right;
		}
	}
}
//挖坑法
int GetPostion(int *a,int left,int right){
	int mid = Getmid(a, left, right);//得到中间数下标
	Swap(&a[left], &a[mid]);//与左边这个数交换

	int temp = a[left];
	while (left < right){
		while (left < right&&a[right] >= temp){
			right--;
		}
		a[left] = a[right];
		while (left < right&&a[left] <= temp){
			left++;
		}
		a[right] = a[left];
	}
	a[left] = temp;
	return left;
}

//递归
void QuickSort(int *a,int left,int right){
	if (left >= right){
		return;
	}
	//int pos = GetPostion1(a, left, right);
	if (right-left > 10){ //小区间优化，减少递归
		int pos = GetPostion(a, left, right);
		QuickSort(a, left, pos - 1);
		QuickSort(a, pos + 1, right);
	}
	else{//数目到了某一值不递归，采用插入排序
		InsertSort(a + left, right - left + 1);//注意，区间可能是后面这段
	}

}

四.非递归

非递归思想要借助栈来实现。利用栈的性质，后进先出，来保存区间。
一开始保存左右两区间，找到prvot位置后，保存两子序列区间，一直调用挖坑法或前后指针法，使区间归为有序，直到栈里没有元素。

代码：

//非递归，用栈存入下标
void QuicksortNonR(int *a, int left, int right){
	Stack stack = Stackinit();
	Stackpush(stack, left);
	Stackpush(stack, right);
	while (!IsEmpty(stack)){
		int end = Stackpop(stack);
		int begin = Stackpop(stack);
		int mid = GetPostion1(a, begin, end);
		if (mid + 1 < end){
			Stackpush(stack, mid + 1);
			Stackpush(stack, end);
		}
		if (mid - 1 > left){
			Stackpush(stack, left);
			Stackpush(stack, mid - 1);
		}
	}
	StackDestory(stack);
}