归并排序算法

Posted 2021-06-30 两片空白

文章目录

• 一.定义
• • 1.归并排序原理
  • 2.归并操作
• 二.实现(递归，非递归)
• • 1.递归
  • 2.非递归
• 三.时间复杂度分析

一.定义

1.归并排序原理

归并排序是建立在归并操作基础上的一种排序方式。归并操作：是指将两个已排序好的子序列合并成一个有序序列的过程。
归并排序基本原理：将大小为N的序列看成N个长度为1的子序列(长度为1的子序列我们认为是有序的)，
接下来将相邻两子序列两两进行归并操作，形成N/2或(N/2)+1个长度为2或1的子序列；
然后再继续进行相邻子序列两两归并操作，如此一直循环，
直到剩下一个长度为N的序列，则该序列就是完成排序后的结果。

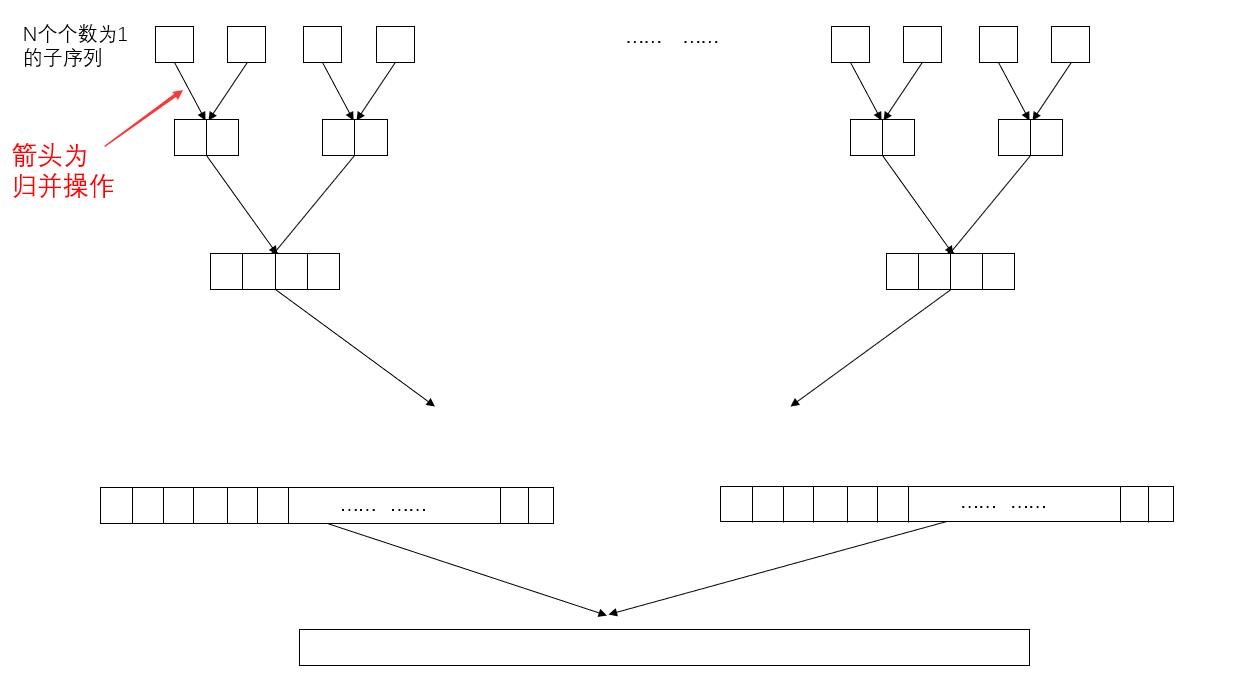
2.归并操作

归并排序核心在于归并操作的实现。
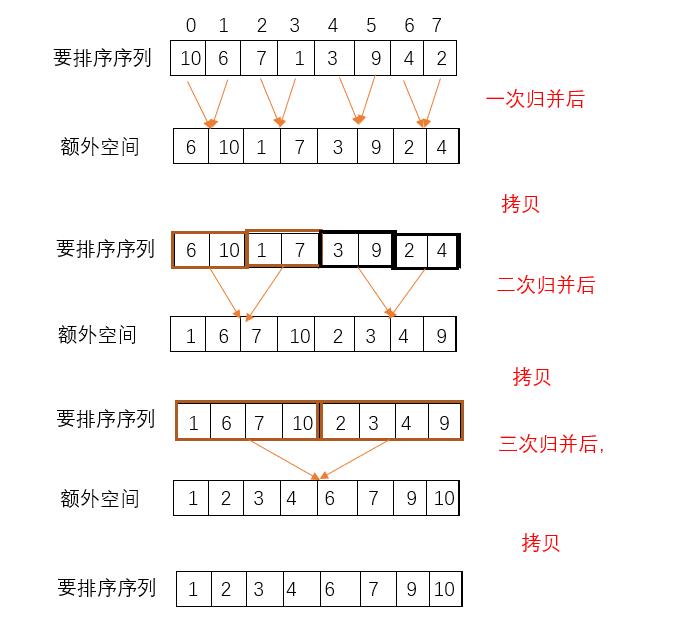
归并操作：首先申请一个额外的空间用于存放两子序列归并后的结果，
接着设置两个指针分别指向两个子序列的开头，比较两指针元素值大小。
将小的放在额外空间额外空间内，并指向小的元素值的指针指向后一个元素。
重复以上过程，直到某个子序列的指针指向改序列结尾。

二.实现(递归，非递归)

归并排序也可使使用分治的思想将原序列划分成两个子序列，递归归并排序这两个子序列。
注意我们在MergeSort函数里开辟的空间，在作为参数传给递归函数，如果过在递归函数里开辟就会频繁的开辟空间释放，影响效率。

1.递归

//归并排序，像二叉树的后续遍历
//取中间，让左右两边有序后，在归并
//开辟一个新数组，归并放到新数组后再拷贝回来。
void _MergeSort(int *a, int left, int right,int *temp){
	if (left >= right){
		return;
	}
	int mid = left + (right - left) / 2;
	//怎么然左右两边有序，递归，最后左右剩下一个就有序了
	_MergeSort(a, left, mid, temp);
	_MergeSort(a, mid + 1, right, temp);
	//再归并，递归回来又有序了,再归并。到最后就全部有序了
	//归并
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int i = begin1;
	//两边中小的放前面，直到一边走完
	while (begin1 <= end1&&begin2 <= end2){
		if (a[begin1] < a[begin2]){
			temp[i++] = a[begin1++];
		}
		else{
			temp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1){
		temp[i++] = a[begin1++];
	}
	while (begin2 <= end2){
		temp[i++] = a[begin2++];
	}
	//拷贝回原数组
	for (int j = left; j <= right; ++j){
		a[j] = temp[j];
	}
}

void MergeSort(int *a, int n){
	int *temp = (int *)malloc(sizeof(int)*n);
	_MergeSort(a, 0, n - 1,temp);
	free(temp);
}

2.非递归

利用循环确定好区间进行归并操作。
将上面图示利用循环写出来。
确定一个间隔gap，一开始为1，将序列分为N个个数为1子序列，将相邻两个子序列归并。在使gap等于2，
将序列分割成N/2或(N/2)+1个长度为2或1的子序列，gap一直以2倍增长。

这样会有两种特殊情况：

1. 要归并的两个序列，前一个序列正好gap个或者不够gap个。
   

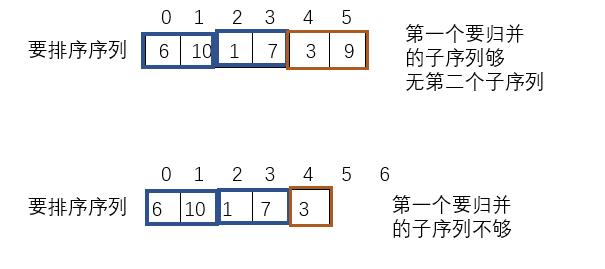
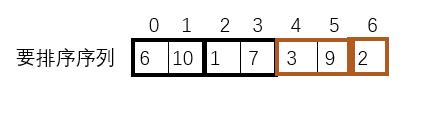
2. 后一个序列不够gap个。
   
   解决办法是：
   前一个序列正好gap个或者不够gap个，不进行归并。
   后一个序列不够gap个，调整后一个子序列区间大小

//划分区间调整
void MergeSortNonR(int *a, int n,int *temp){
	int gap = 1;
	while (gap < n){
		for (int i = 0; i < n; i += 2 * gap){
			int j = i;//用作开辟空间下标
			//前面子序列区间
			int begin1 = i;
			int end1 = i + gap - 1;
			
			//后面这个区间再前面区间基础上加gap
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;
			
			//调整，第一个区间数不够或者正好够，不归并
			if (end1>=n - 1){
				break;
			}

			//到这第二个区间肯定有数
			//第二个区间数不够，调整区间
			if (end2 >= n){
				end2 = n - 1;//调整到最后
			}
			//归并
			while (begin1 <= end1&&begin2 <= end2){
				if (a[begin1] < a[begin2]){
					temp[j++] = a[begin1++];
				}
				else{
					temp[j++] = a[begin2++];
				}

			}
			while (begin1 <= end1){
				temp[j++] = a[begin1++];
			}
			while (begin2 <= end2){
				temp[j++] = a[begin2++];
			}
			for (int k = i; k <= end2; k++){
				a[k] = temp[k];
			}


		}
		gap *= 2;
	}

}

三.时间复杂度分析

由递归可以看出递归每趟归并要O(N)的时间复杂度，递归深度为O(logN),因此时间复杂度为O(NlogN).但是归并排序需要开辟额外的空间，空间复杂度为O(N)。