探寻宝藏 算法设计与分析课设 c语言代码 + 思路详解

Posted 2021-06-30 林深时不见鹿

目录

• • 1、题目
  • 2、思路1
  • 3、代码1
  • 4、思路2
  • 5、代码2

1、题目

传说HMH大沙漠中有一个M*N迷宫，里面藏有许多宝物。某天，Dr.Kong找到了迷宫的地图，他发现迷宫内处处有宝物，最珍贵的宝物就藏在右下角，迷宫的进出口在左上角。当然，迷宫中的通路不是平坦的，到处都是陷阱。Dr.Kong决定让他的机器人卡多去探险。

但机器人卡多从左上角走到右下角时，只会向下走或者向右走。从右下角往回走到左上角时，只会向上走或者向左走，而且卡多不走回头路。（即：一个点最多经过一次）。当然卡多顺手也拿走沿路的每个宝物。

Dr.Kong希望他的机器人卡多尽量多地带出宝物。请你编写程序，帮助Dr.Kong计算一下，卡多最多能带出多少宝物。

输入

第一行： K 表示有多少组测试数据。

接下来对每组测试数据：

第1行: M N

第2~M+1行：Ai1 Ai2 ……AiN (i=1,…..,m)

【约束条件】

2≤k≤5 1≤M, N≤50 0≤Aij≤100 (i=1,….,M; j=1,…,N)

所有数据都是整数。 数据之间有一个空格。

输出

对于每组测试数据，输出一行：机器人卡多携带出最多价值的宝物数

样例输入

2
2 3
0 10 10
10 10 80
3 3
0 3 9
2 8 5
5 7 100

样例输出

120
134

2、思路1

假设出发点为A终点为B ，题目要求从A->B，然后再从B->A，求出这两条路径上取得的最大的和（路径不能重复）。我们可以假设同时从A出发，得到两条不同路径，这是相同的效果，相当于从A->B一共走了两次。

我们首先考虑只走一次。

只走一次：

状态表示： f[i,j]表示所有从(1,1)走到(i,j)的路径之和的最大值

状态转移：

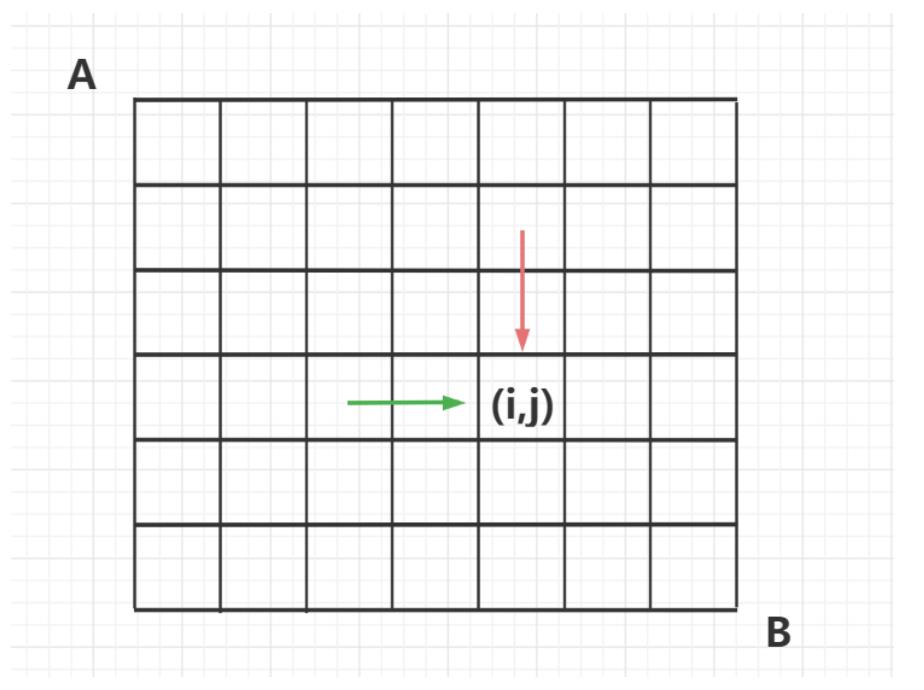
由于限制了只会向下走或者向右走，因此到达(i,j)有两条路径

• 从上方转移过来，f[i][j] = f[i][j-1]+ a[i][j]
• 从左方转移过来，f[i][j] = f[i-1][i]+ a[i][j]

因此，状态计算方程为： f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j]， 从向右和向左两条路径中选择路径之和最大的转移过来，再加上a[i][j]的值。

现在我们考虑走两次。

走两次:

状态表示： f[i1,j1,i2,j2]表示所有从(1,1),(1,1)分别走到(i1,j1),(i2,j2)的路径之和的最大值。

状态计算：

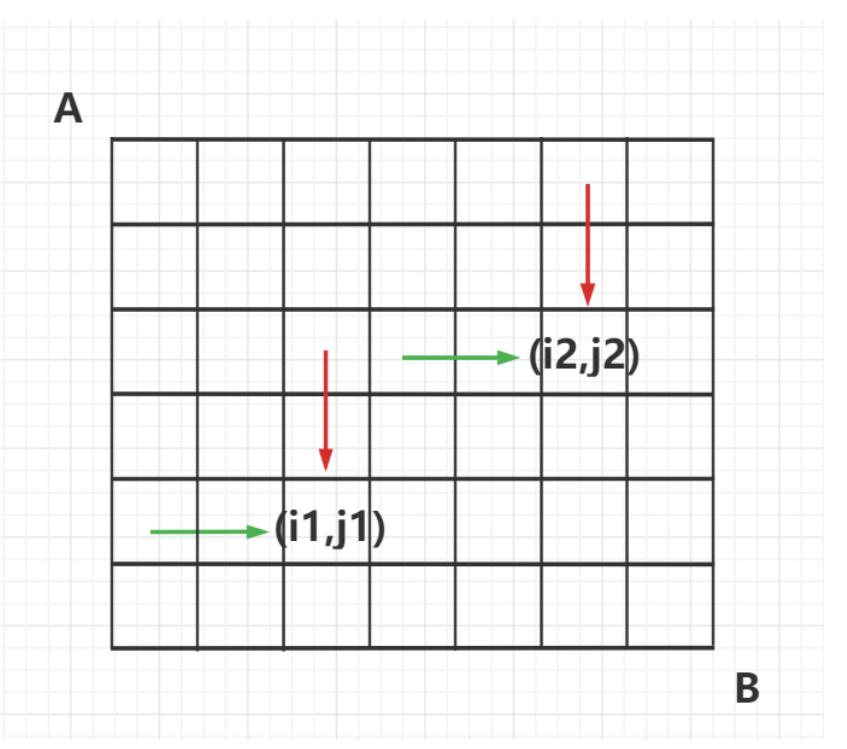
从(1,1),(1,1)分别走到(i1,j1)，(i2,j2)的前一步共有四条路径：

• 第一条：下 第二条：下

  f[i1][j1][i2][j2] = f[i1-1]][j1][i2-1][j2] + a[i1][j1] + a[i2][j2]

• 第一条：下 第二条：右

  f[i1][j1][i2][j2] = f[i1-1][j1][i2][j2-1] + a[i1][j1] + a[i2][j2]

• 第一条：右 第二条：下

  f[i1][j1][i2][j2] = f[i1][j1-1][i2-1][j2] + a[i1][j1] + a[i2][j2]

• 第一条：右 第二条：右

  f[i1][j1][i2][j2] = f[i1][j1-1][i2][j2-1] + a[i1][j1] + a[i2][j2]

因此，状态计算方程为： f[i1][j1][i2][j2] = max(f[i1][j1][i2][j2],f[i1-1][j1][i2][j2-1],f[i1][j1-1][i2-1][j2],f[i1][j1-1][i2][j2-1]) + a[i1][j1] + a[i2][j2]。

注意点：

因为一个点只能走一次，包括终点也是如此。因此，我们考虑终点的前一步，最后再加上终点的值。而终点的前一步共有两种可能，如下：

故最后的答案取值为：max(f[n][m-1][n-1][m],f[n-1][m][n][m-1]) + a[n][m]。

时间复杂度分析：4重循环，因此时间复杂度为$O(n\ast n\ast m\ast m)$ 。

空间复杂度分析： 定义状态为4维，因此空间复杂度为$O(n\ast n\ast m\ast m)$ 。

3、代码1

#include<stdio.h>
#include<string.h>

const int N = 55;
int a[N][N];
int f[N][N][N][N]; 

int max(int a,int b)
{
	return a>b?a:b;
} 

int main()
{
	int k,n,m;
	scanf("%d",&k);
	while(k--)
	{
		scanf("%d%d",&n,&m);
		memset(f,0,sizeof(f));
		memset(a,0,sizeof(a));
		for(int i = 1; i <= n; i++)
		   for(int j = 1; j <= m; j++)
		     scanf("%d",&a[i][j]);
		for(int i1 = 1; i1 <= n; i1++)
		    for(int j1 = 1; j1 <= m; j1++)
				for(int i2 = 1; i2 <= n; i2++)
					for(int j2 = 1; j2 <= m; j2++)
					{
						if(i1 == i2 && j1 == j2)  continue;  //走到同一格子
						int &x = f[i1][j1][i2][j2];
						int t = a[i1][j1] + a[i2][j2]; 
						x = max(x,f[i1-1][j1][i2-1][j2]+t);
						x = max(x,f[i1-1][j1][i2][j2-1]+t);
						x = max(x,f[i1][j1-1][i2-1][j2]+t);
						x = max(x,f[i1][j1-1][i2][j2-1]+t); 					
					}
		printf("%d\\n",max(f[n][m-1][n-1][m],f[n-1][m][n][m-1]) + a[n][m]);	  
	}
	return 0;
} 

4、思路2

第一种思路的时间复杂度为$O(n\ast n\ast m\ast m)$ ，当n和m很大时，这样的效率显然我们是不能接受的。有没有一种方法可以降低时间复杂度那？答案时有的。

这道题的关键在于如何处理” 同一个格子只能走一次 “？

我们发现只有在i1 + j1 == i2 +j2时，两条路径的格子才可能重合 。我们让 k = i1 + j1 == i2 +j2，两个人同时从A出发，每个人走的步数和是一样的。

新的状态表示：f[k, i1, i2]表示所有从(1,1),(1,1)分别走到(i1,k-i1), (i2,k-i2)的路径之和的最大值，k表示两条路线当前走到的格子的横纵坐标之和（或者说两个人都走了k步）。

k = i1 + j1 = i2+ j2

因此把状态由f[i1][j1][i2][j2]优化成三维f[k][i1][i2]等价于f[i1][k−i1][i2]k−i2]

状态计算：

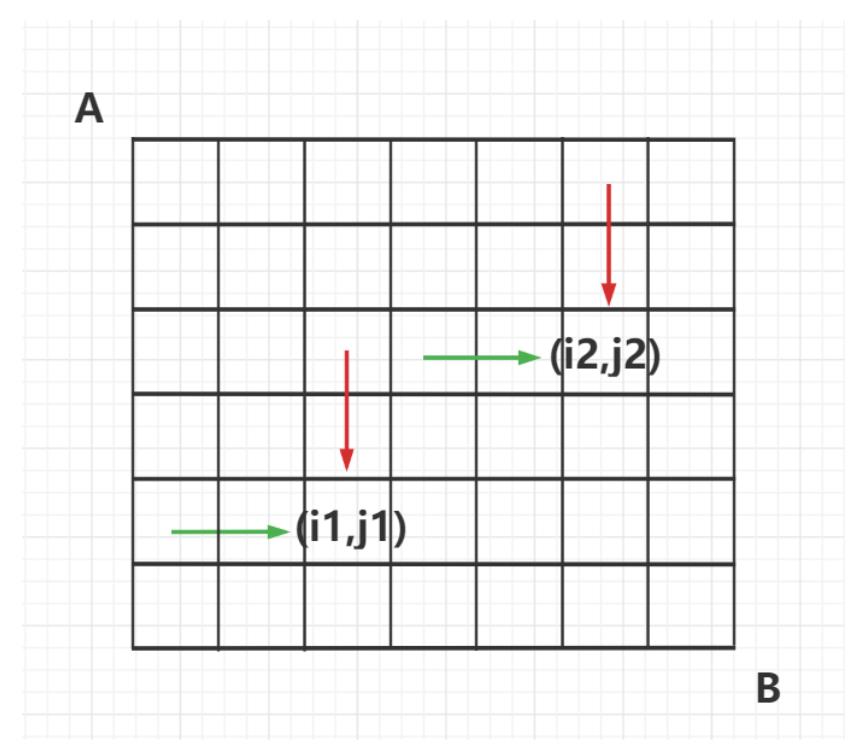
从(1,1),(1,1)分别走到(i1,j1)，(i2,j2)的前一步共有四条路径：

• 第一条：下 第二条：下

  f[i1-1]][j1][i2-1][j2] == f[k-1][i1-1][i2-1];

• 第一条：下 第二条：右

  f[i1-1][j1][i2][j2-1] == f[k-1][i1-1][i2];

• 第一条：右 第二条：下

  f[i1][j1-1][i2-1][j2] == f[k-1][i1][i2-1];

• 第一条：右 第二条：右

  f[i1][j1-1][i2][j2-1] == f[k-1][i1][i2];

我们解释上面的一种状态:

f[i1-1]][j1][i2-1][j2] == f[k-1][i1-1][i2-1]：代表两个人都走了k-1步，A从(i1-1,j1)走到(i1,j1),B从(i2-1,j2)走到(i2,j2)。

因此，状态计算方程为： f[k][i1][j1] = max(f[k-1][i1-1][i2-1],f[k-1][i1-1][i2],f[k-1][i1][i2-1],f[k-1][i1][i2]) + a[i1][j1] + a[i2][j2]。

注意点： 同思路1一样

最终的答案为： max(f[n+m-1][n][n-1],f[n+m-1][n-1][n])+a[n][m]

时间复杂度分析：3重循环，因此时间复杂度为$O((n+m)\ast n\ast n)$ 。

空间复杂度分析： 定义状态为3维，因此空间复杂度为$O((n+m)\ast n\ast n)$ 。

完整分析图示：

5、代码2

#include<stdio.h>
#include<string.h>

const int N = 55;
int a[N][N];
int f[2*N][N][N]; 

int max(int a,int b)
{
	return a>b?a:b;
} 

int main()
{
	int k,n,m;
	scanf("%d",&k);
	while(k--)
	{
		scanf("%d%d",&n,&m);
		memset(f,0,sizeof(f));
		memset(a,0,sizeof(a));
		for(int i = 1; i <= n; i++)
		   for(int j = 1; j <= m; j++)
		     scanf("%d",&a[i][j]);
		for(int k = 2; k <= n+m; k++)
		    for(int i1 = 1; i1 <= n; i1++)
				for(int i2 = 1; i2 <= n; i2++)				
				{
				 	int j1=k-i1,j2=k-i2;
				 	if(i1 >= 1 && j1 <= n && i2 >=1 && j2 <=m)
				 	{
					    if(i1 == i2) continue;
						int &x=f[k][i1][i2];
						int t = a[i1][j1] + a[i2][j2]; 
						x=max(x,f[k-1][i1-1][i2-1]+t);
                		x=max(x,f[k-1][i1-1][i2]+t);
               			x=max(x,f[k-1][i1][i2-1]+t);
                		x=max(x,f[k-1][i1][i2]+t);
					} 					
				}
		printf("%d\\n",max(f[n+m-1][n][n-1],f[n+m-1][n-1][n])+a[n][m]);	  
	}
	return 0;
}