正态分布离群值检验——偏度与峰度方法
Posted zhuo木鸟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了正态分布离群值检验——偏度与峰度方法相关的知识,希望对你有一定的参考价值。
本文主要参考 GB/T 4883-2008 的 8.2.2 和 8.2.3 条款。
记样本为 x 1 , x 2 , ⋯ , x n x_1, x_2, \\cdots, x_n x1,x2,⋯,xn,n 为样本容量,按照升序排序,得到持续统计量为 x ( 1 ) , x ( 2 ) , ⋯ , x ( n ) x_{(1)}, x_{(2)}, \\cdots, x_{(n)} x(1),x(2),⋯,x(n)
偏度检验法——用于单侧检验
- 计算偏度统计量
b
s
b_s
bs 的值为:
b s = n ∑ i = 1 n ( x i − x ˉ ) 3 [ ∑ i = 1 n ( x i − x ˉ ) 2 ] 3 / 2 b_s = \\frac{\\sqrt{n} \\sum_{i=1}^{n} (x_i - \\bar{x}) ^3} {[\\sum_{i=1}^n (x_i - \\bar{x})^2]^{3/2}} bs=[∑i=1n(xi−xˉ)2]3/2n∑i=1n(xi−xˉ)3 - 择定一个检验水平
α
\\alpha
α,在表中 A.4 查出临界值
b
s
(
n
)
b_s(n)
bs(n),表 A.4 收录如下:
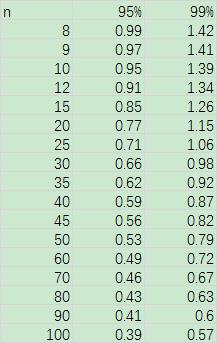
如果样本数 n 不在临界值表中,则采用 spline 三次插值法,用插值法求取临界值。 - 对于上侧检验,当 b s > b s ( n ) b_s > b_s(n) bs>bs(n) 时,则判断 x ( n ) x_{(n)} x(n) 为歧离值,所谓歧离值,就是有概率会成为离群值的数。之后,再择定一个更为严格的剔除水平,再次根据表或插值法,找出临界值,再另行判断。若依旧满足 b s > b s ( n ) b_s > b_s(n) bs>bs(n),则 x ( n ) x_{(n)} x(n) 为离群值。
- 对于下侧检验,则用 − b s > b s ( n ) -b_s > b_s(n) −bs>bs(n) 来判断,其他照旧。
Python 实现
将上述表格存储于一个叫 dixon_critical_value.xlsx 的 Excel 表的,一个叫 “偏度检验” 的工作簿中:
import numpy as np
import pandas as pd
from scipy import interpolate
def perform_skewness_test(x, lower=True, alpha=0.95):
if isinstance(x, pd.Series) or isinstance(x, pd.DataFrame):
x = x.astype('float').values
if isinstance(x, list):
x = np.array(x)
if alpha != 0.95:
raise(Exception('置信水平可选择:0.95'))
# 样本个数
n = len(x)
if n < 8:
raise(Exception('偏度检验的要求样本数必须大于 8'))
dection_level = 0.95
deletion_level = 0.99
numerator = np.sqrt(n)*sum((x-np.mean(x))**3)
dominator = np.power(sum((x-np.mean(x))**2), 3/2)
bs = numerator/dominator
path = r'./dixon_critical_value.xlsx'
critical_values = pd.read_excel(path, sheet_name='偏度检验')
if n <= 12:
n_interpolate = np.arange(8, 13)
n_list = critical_values['n'].iloc[:4].values
values_dect = critical_values[dection_level].iloc[:4].values
values_dele = critical_values[deletion_level].iloc[:4].values
f_dect = interpolate.interp1d(n_list, values_dect, kind='cubic')
f_dele = interpolate.interp1d(n_list, values_dele, kind='cubic')
elif n <= 50:
n_interpolate = np.arange(8, 51)
n_list = critical_values['n'].iloc[:12].values
values_dect = critical_values[dection_level].iloc[:12].values
values_dele = critical_values[deletion_level].iloc[:12].values
f_dect = interpolate.interp1d(n_list, values_dect, kind='cubic')
f_dele = interpolate.interp1d(n_list, values_dele, kind='cubic')
elif n <= 100:
n_interpolate = np.arange(8, 100)
n_list = critical_values['n'].iloc[:17].values
values_dect = critical_values[dection_level].values
values_dele = critical_values[deletion_level].values
f_dect = interpolate.interp1d(n_list, values_dect, kind='cubic')
f_dele = interpolate.interp1d(n_list, values_dele, kind='cubic')
values_dect = f_dect(n_interpolate)
values_dele = f_dele(n_interpolate)
critical_value = values_dect[n-8]
if -bs > critical_value and lower:
straggler = x[0]
elif bs > critical_value and lower==False:
straggler = x[-1]
else:
print('无离群值')
return x
critical_value = values_dele[n-8]
# 根据剔除水平,检测出离群值
if np.abs(bs) > critical_value:
outlier = straggler
print('样本中带有离群值值: ', outlier)
x = np.delete(x, np.where(x==outlier))
return x
else:
print('样本中带有歧离值: ', straggler)
return x
if __name__ == '__main__':
#检验案例
x = np.array([1125, 1248, 1250, 1259, 1273, 1279, 1285, \\
1285, 1293, 1300, 1305, 1312, 1315, 1324, 1325, 1350])
x_1 = perform_skewness_test(x, alpha=0.95, lower=True)
峰度检验法——用于双侧检验
- 计算峰度统计量
b
k
b_k
bk 的值为:
b k = n ∑ i = 1 n ( x i − x ˉ ) 4 [ ∑ i = 1 n ( x i − x ˉ ) 2 ] 2 b_k = \\frac{n \\sum_{i=1}^n (x_i - \\bar{x})^4} {[\\sum_{i=1}^n (x_i - \\bar{x})^2]^2} bk=[∑i=1n(xi−xˉ)2]2n∑i=1n(xi−xˉ)4 - 根据表 A.5,和择定的检验水平
α
\\alpha
α,择定一个临界值
b
k
(
n
)
b_k(n)
bk(n),表 A.5 收录如下。若无对应的临界值,则需要根据一元三次插值法,用插值替代临界值。
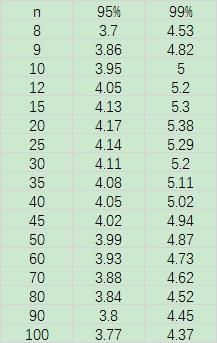
- 当 b k > b k ( n ) b_k > b_k(n) bk>bk(n) 时,则认为离均值 x ˉ \\bar{x} xˉ 最远的数为歧离值。
- 再次择定一个更为严格的剔除水平,根据表 A.5,找出临界值,再次比较。若依旧满足 b k > b k ( n ) b_k > b_k(n) bk以上是关于正态分布离群值检验——偏度与峰度方法的主要内容,如果未能解决你的问题,请参考以下文章