统计世界:相关就好
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了统计世界:相关就好相关的知识,希望对你有一定的参考价值。
为什么要学习统计学
图表的玄机:既可以揭露谎言,也可以瞒天过海
一、操作横坐标
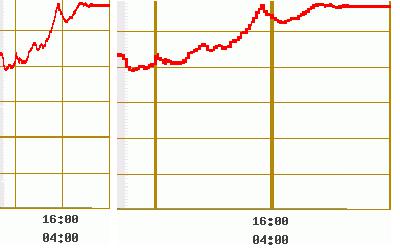
上面俩张图描述的是相同时间段的变化,左边的看起来是极速上升,右边的看起来缓慢上升。
实际上,这是同一张图,只不过右边的图是横向拉长了。
图表的拉伸和缩放,可以使得展示的信息不同。
因此,在观察统计图时要万分注意,重要的东西要用心看。
二、操作纵坐标
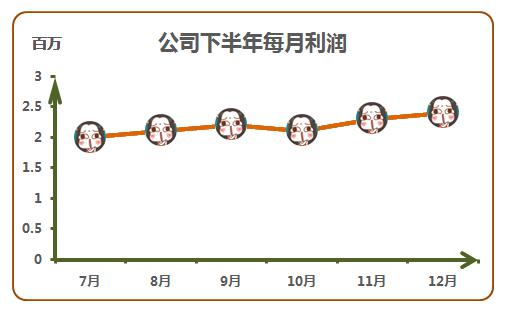
操纵后:
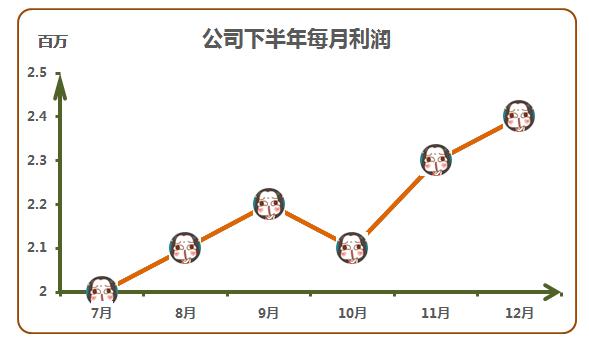
大家来找茬:
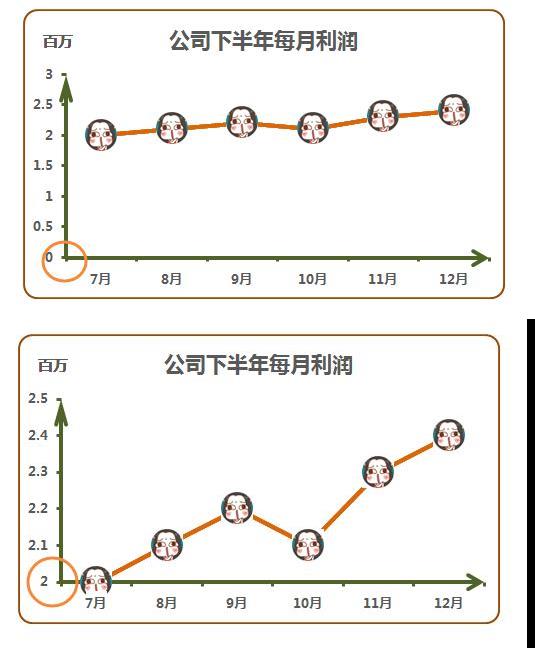
改变最大、最小值,图表的变化就大了。
如果某天我们看图表,图的坐标轴的最小值是非0数值,我们就应该知道是怎么回事,有人再搞小动作!
这是把数据波动增大的方法,还有一种把数据波动减少的方法,就是数据取值按照等比数列,而不是等差数列。
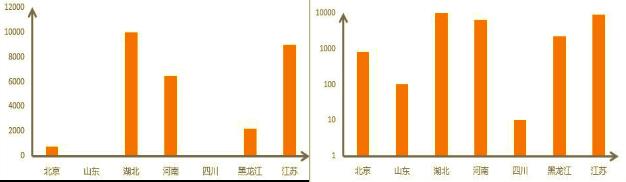
第三、数据标准化
这种方法不属于作弊,是为了不同的指标进行对比和加权,是一种常用的数据处理方法。
基本思想是,将数据按比例缩放,使得落入一个小的特定区间。
比如,按照某种公式将所有数据标准化映射到 [0, 1] 区间。
最简单的方法:直接将数据除以 10 的 N 次方(100、1000、1000),N取决于具体数据的最大值。
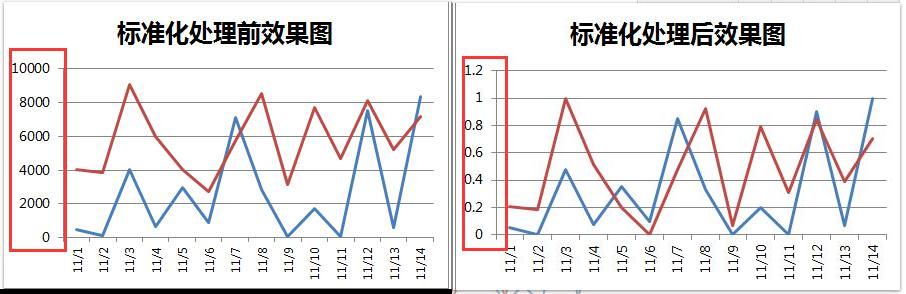
上图将数据缩小了 10000 倍,进行标准化处理,便于指标之间进行比较和加权。
第四、捏造趋势
一种常见的图表作弊方式。
假设有一组公司的财务数据:10、1、20、3、30、4、50,这组数据的波动性很大。
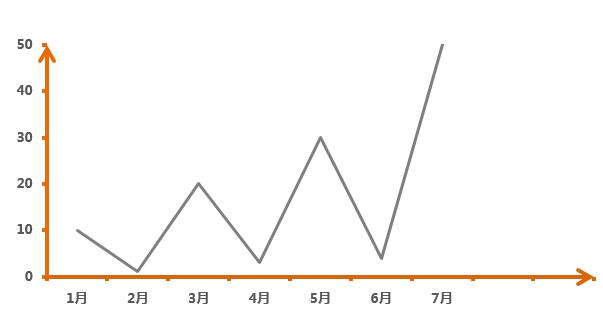
公司的财务数据这么不稳定,咋办?
没关系,如果我只挑选奇数项······
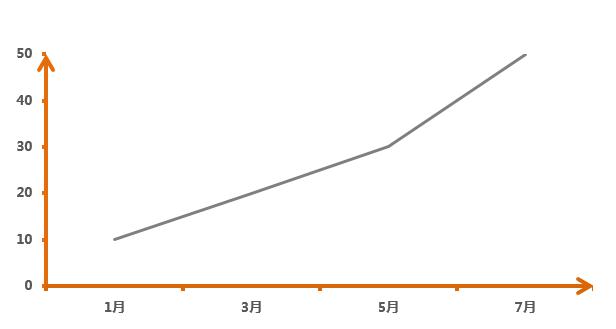
咳咳,照这样下去,明年公司就可以上市了。
所以,如果数据波动性很大,只挑选X轴中对自己有利的数据,就会改变数据的趋势。
被混淆的因果关系:让世界讲得通,学会分析事物之间的各种关系
话说1995年,美国有个叫麦克阿瑟·惠勒的中年男子,单枪匹马抢了两家银行。
银行的人没难为他,要钱给钱。电影里一般抢银行的都带个头套,但是惠勒没有采取任何伪装措施,他甚至还对着监控摄像头笑了笑,抢完银行就愉快地回家了。
当天晚上警察就抓住了他,并且出示了监控录像带的证据。惠勒感到很震惊。
惠勒说,不对啊,我已经在脸上抹了柠檬汁啊!
也许他听人说过柠檬汁可以隐形这个知识。但他显然误解了“隐形”的意思。
再看一个例子,研究发现:越是成功人士(收入越高),睡眠时间越短。
惠勒(一知半解的人)肯定会想,今晚就睡2个小时,明天薪水就过亿了。
背后的逻辑是:只要减少睡眠,收入就会增加,就会成功。
实际上,这里推理有严重的逻辑错误,把相关关系当作了因果关系。
- 相关关系:A 越多,B 越多
- 因果关系:A 越多,导致 B 越多
如果没有进一步的调查和理论,相关关系是推理不出因果关系的 — 睡眠少和成功存在相关关系,但不能说睡眠少导致了成功。
A 越多,B 越多,这种相关关系可能存在4种可能:(A睡眠,B收入,C年龄)
- A 导致 B:更少睡眠导致收入增加
- B 导致 A:收入增加导致睡眠减少
- A、B 同时被 C 导致:随着年龄增长,人对睡眠需求减少,因此睡眠少,同时年龄大的人,往往经验、人脉、知识更多,也自然收入更多
- A、B 没有任何关系:美国、西欧等经济发达,导致收入高,同时他们爱吃牛排,导致睡眠需求减少
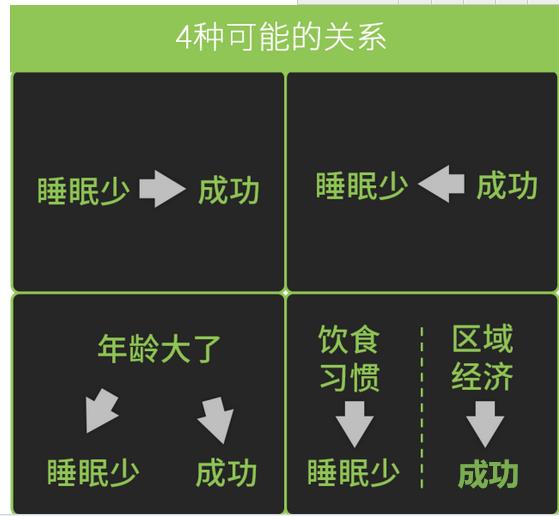
因果关系只是其中的2种可能(第一种、第二种)。
所以,类似【相关关系:A 越多,B 越多】不一定是简单的因果关系,但因果关系一定是相关关系。
我们学习统计学,就是让世界讲得通,学会分析事物之间的各种关系。
统计小百科
统计是什么
统计是一门收集数据、处理和分析数据、解释数据并从数据中得出结论的科学。
统计学体系:
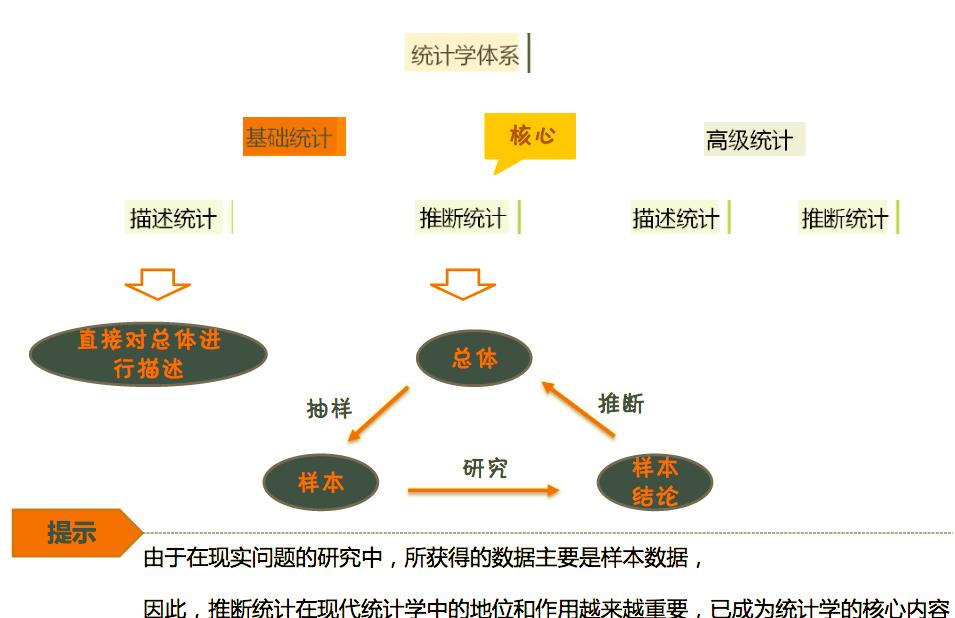
一、什么是描述统计?
描述统计的重点是描述一组数据的特征。
主要分为图表描述、统计量描述:
- 图表描述:条形图、直方图、饼图、散点图······
- 统计量描述:集中趋势(平均数、中位数、众数)、离中趋势(极差、方差、标准差、变异系数)、偏态和峰态(偏态系数、峰态系数)。
比如,
- 散点图:描述一组数据的离散程度(图表描述)
- 平均数:描述一组数据的集中程度(统计量描述)
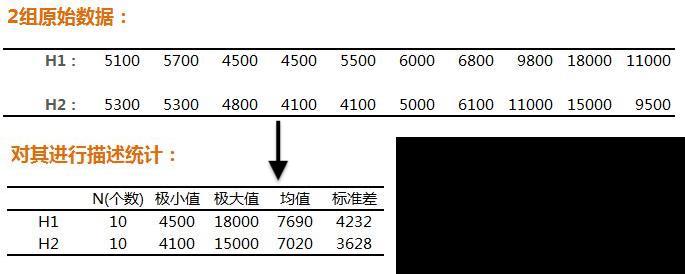
二、什么是推断统计?
推断统计是研究如何利用样本数据来推断总体特征的统计方法。
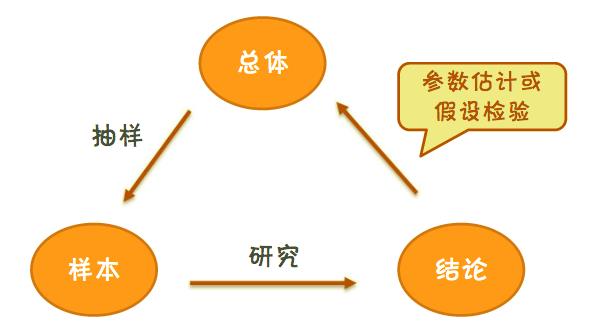
统计推断原理:
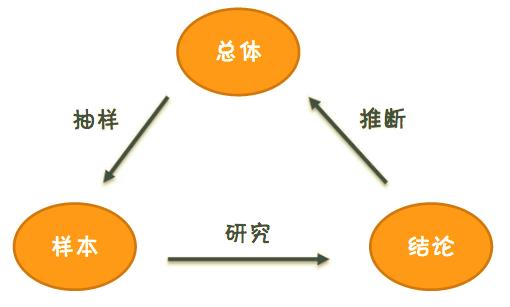
比如,要对产品质量进行检测,也不可能对每个产品都进行检测,这就需要抽取样本,对个体进行测量,而后根据获得的结论对总体特征进行推断。
这就是推断统计要解决的问题。
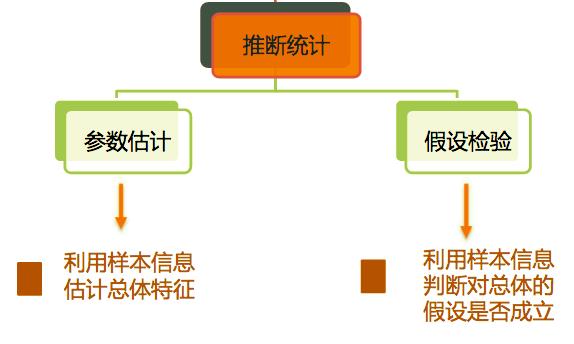
- 参数估计:利用样本信息估计总体特征
- 假设检验:利用样本信息判断对总体的假设是否成立
【待续,未完】
概率和机会
概率描述了某件事情出现的可能性大小。例如,就是用概率值表示天气现象出现的可能性的大小,它所提供的,不是某种天气现象是否出现,而是某种气象出现的可能性有多大。
一、概率和机会是什么关系?
概率描述了某件事情发生的机会。比如,在天气预报中,会提到降水概率。
如果降水概率是 90%,那就很可能下雨,但如果是 10%,就不大可能下雨。
这种概率不可能超过 100%,也不可能少于 0%,换言之,概率是在 [0, 1] 之间的一个数,它说明了某件事情发生的机会有多少。
如果你对别人说,周末去公园的概率是80%,这时候,你无法精确说出,为什么是80%,而不是81%、79%。
其实你想说的是,你很想去,但不完全肯定,所以,概率无法精确推断,但是,有些概率是可以估计的。
比如,扔硬币的概率是 1 2 \\frac{1}{2} 21。
二、什么是条件概率?
一个家庭有俩孩子,请问都是女孩的概率是多少?
- 1 2 ∗ 1 2 = 1 4 \\frac{1}{2}*\\frac{1}{2}=\\frac{1}{4} 21∗21=41。
一个家庭有俩孩子,知道一个是女孩,另一个也是女孩的概率?
- 一个是女孩,就有 [女孩男孩]、[男孩女孩]、[女孩女孩],所以是 1 3 \\frac{1}{3} 31。
一个家庭有俩孩子,已知大孩子是女孩,问小的也是女孩的概率?
- 1 2 \\frac{1}{2} 21,只有俩种可能。
问题2、3的条件看上去很相似,但其实是不一样的。
同样是问这个家庭的俩个孩子都是女孩的概率,问题1因为没有告诉你更多额外的信息,因此答案是 1 4 \\frac{1}{4} 41。
但问题2和问题3却附加了一些信息或条件,因此概率就发生了变化而不再是 1 4 \\frac{1}{4} 41。
我们将这种在某种条件或信息下,对事件发生的可能性大小,称为条件概率。
三、相关事件和独立事件
如果几个事件互有影响,则为相关事件。
即一件事件发生与否,会影响另一件事件的发生的概率。比如,酒驾和车祸是相关事件。
如果几个事件互不影响,则为独立事件。
即无论其他事件发生与否,某个事件的发生概率总是保持不变。
四、互斥事件
互斥事件是指,事件A与事件B不可能同时发生,互斥事件意味着AB同时发生的概率为0,即 P ( A B ) = 0 P(AB)=0 P(AB)=0。
比如,班长只有一个,选了小白,就不能选小黑。
变量和常量
变量和常量,都是统计学研究中的对象特征,在数量指标中:
- 不变的数量的指标称为常量或常数
- 可变的数量的指标称为变量
一、连续变量、离散变量
变量,按变量值是否连续,分为连续变量、离散变量。
离散变量,是指其数值只能用自然数或整数单位计算。比如,企业个数、职工人数等。
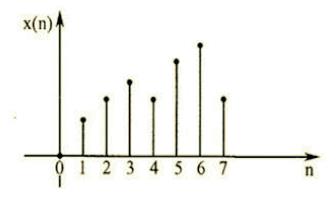
连续变量,是指一定区间内可以任意取值的变量,其数值是连续不断的。例如,身高、血压、体重等。
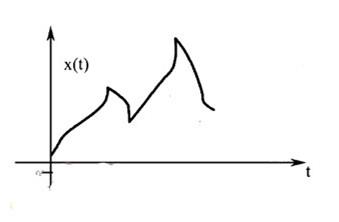
那区分连续变量、离散变量最简单的方法是什么?
- 连续变量:是一直叠加上去的,是逐渐增加的,比如身高
- 离散变量:是对所有统计的对象计数,增长量是非固定,不是逐渐增长,比如公司人数
二、定性变量、定量变量
变量按变量值是否能量化,分为定性变量与定量变量。
- 定量变量:像人的体量,男女生的人数等,可以由数字量化的变量就称为定量变量。
- 定性变量:像性别、观点之类的无法用数字来表示的变量,就称为定性变量。
数据的几种类型
一、数据按计量层次,分为数值型、分类型、顺序型。
- 数值型:可以由具体的数值来计量,是对事物的精确测度,比如,收入xx元
- 分类型:性别按男、女分类,药物反应按阴性、阳性,血型按O、A、B、AB分类
- 顺序型:各类别之间有程度的差别,例如奖学金有一等、二等、三等奖励程度分类
不同类型的数据之间是可以相互转换的。
-
数值型数据可以转为分类型数据。
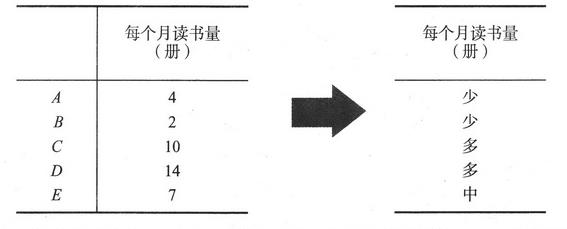
在变换时,少、中、多之间的分界线是多少,需要我们做判断。 -
分类型数据转为数值型数据
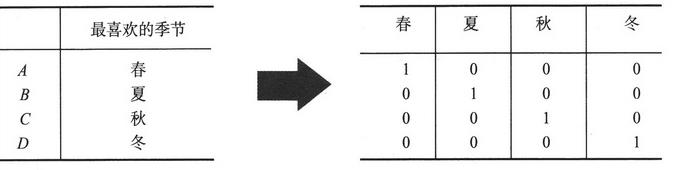
如此,变换星期可采用7列,变换月份可采用12列,这种数据转换的目的,是为了使分类数据尽可能的量化,以便进行更好的数据分析。
二、数据按时间状况,分为截面数据和时序数据。
- 截面数据,是指在同一时间,由不同的统计单位,和相同统计指标组成的一组数据,例如股票数据。
- 时序数据,是在不同时间点上收集到的数据,这类数据反映的是某一现象随时间的变化状态或程度。
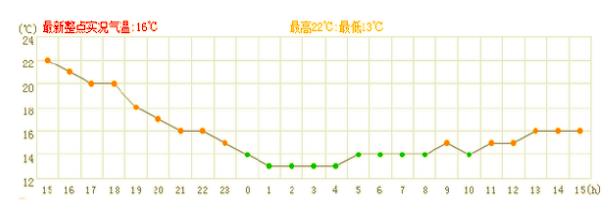
易混淆的统计术语
一、绝对数、相对数
- 绝对数:是反映客观现象总体,在一定时间、地点条件下的总规模、总水平的综合性指标。
- 相对数:是指由俩个有联系的指标,对比计算而得到的数值。比如,7成。
二、频数和频率
- 频数:是指一组数据中个别数据重复出现的次数。比如,某校A班学生共50名,按性别进行分组,分为男与女俩个组别,男同学的频数为30,女同学的频数为20。
- 频率:是每个小组的频数与数据总和的比例,代表的是某组在总体中出现的频繁程度。比如,某校A班学生共50名,按性别进行分组,分为男与女俩个组别,男同学的频数为60%,女同学的频数为40%。
所以,频数是绝对数,频率是相对数。
三、百分比、百分点
- 百分比:表示一个数是另一个数的百分之几,也称百分率或百分数,通常采用百分号(%)来表示,TA属于相对数。
- 百分点:是指以百分数的形式表示的相对指标的变动幅度。一个百分点 = 1%。
四、比例、比率
- 比例:是指在总体中,各部分数值占全部数值的比重,反映的是总体的构成和结构。比如A班有学生50人,男生25人,女生25人,则男生比例是 1 2 \\frac{1}{2} 21。
- 比率:是不同类别数值的对比,反映的是一个整体中各部分之间的关系。比如A班有学生50人,男生25人,女生25人,则男、女比例是 1 : 1 1:1 1:1。
五、倍数、番数
- 倍数:是一个数除以另一个数所得的商
- 番数:是指原来数量的2的N次方倍,比如翻一番 = 原来的2倍、翻俩番 = 原来的4倍
六、同比、环比
- 同比:目的是为了与历史同时期进行比较,该指标主要反映的是事物发展的相对情况,比如2018年8月和2020年8月。
- 环比:目的是为了与前一个统计时期,进行比较得到的数值,该指标主要反映的是事物逐期发展的情况,比如2018年8月和2018年9月。
描述统计:图表描述
定类数据的图表描述
定序数据的图表描述
定距数据的图表描述
多变量数据的图表描述
如何选择合适的图表
有效图表的的几个基本要素
增强图表达力的几种方法
可视化图表的几个注意事项
描述统计:统计量描述
集中趋势:数据分布特征的描述
离中趋势:数据分布特征的描述
偏态和峰态:数据分布特征的描述
数据标准化的几种方法
抽样
数据的收集和整理
收集数据是的误差
常用的抽样方法
设计调查问卷的原则
推断统计:参数估计
概率和概率分布
点估计和区间估计
总体参数的估计
三大抽样分布
样本统计量的抽样分布
推断统计:假设检验
假设检验的原理
原假设和备择假设的确定
假设检验的基本概念
总体均值的检验:Z检验
总体均值的检验:T检验
总体方差和总体比例的检验
相关与回归分析
统计基础:什么是相关关系
统计基础:相关分析和回归分析
统计基础:如何求最佳的拟合线
统计基础:相关系数
SPSS实操:相关分析案例
SPSS实操:线性回归案例
SPSS实操:曲线线性回归案例
方差分析
统计基础:为什么要进行方差分析
统计基础:方差分析概述
统计基础:单因素方差分析
统计基础:双要素方差分析
SPSS实操:单因素方差分析案例
SPSS实操:双因素方差分析案例
主成分分析
统计基础:主成分分析原理
统计基础:主成分分析的几何解释
SPSS实操:主成分分析的经典案例
SPSS实操:用主成分分析法确定权重
SPSS实操:用主成分分析法确定综合盈利
因子分析
统计基础:因子分析原理
SPSS实操:影响国民经济发展的因子分析
SPSS实操:因子分析在人才招聘中的应用
聚类分析
统计基础:认识聚类分析
统计基础:聚类分析概述
SPSS实操:系统聚类案例分析
SPSS实操:K均值聚类案例分析
以上是关于统计世界:相关就好的主要内容,如果未能解决你的问题,请参考以下文章