表盘识别基于Hough变换实现指针式仪表识别（倾斜矫正）

Posted 2021-06-30 博主QQ2449341593

一、简介

霍夫变换(Hough Transform)是图像处理中的一种特征提取技术，它通过一种投票算法检测具有特定形状的物体。该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。霍夫变换于1962年由Paul Hough 首次提出[53]，后于1972年由Richard Duda和Peter Hart推广使用[54]，经典霍夫变换用来检测图像中的直线，后来霍夫变换扩展到任意形状物体的识别，多为圆和椭圆。

霍夫变换运用两个坐标空间之间的变换将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为统计峰值问题，上一节中已经介绍了车道的直线特征，本节中介绍hough变换检测直线的原理和检测结果。

我们知道，一条直线在直角坐标系下可以用y=kx+b表示, 霍夫变换的主要思想是将该方程的参数和变量交换，即用x,y作为已知量k,b作为变量坐标，所以直角坐标系下的直线y=kx+b在参数空间表示为点(k,b)，而一个点(x1,y1)在直角坐标系下表示为一条直线y1=x1·k+b，其中(k,b)是该直线上的任意点。为了计算方便，我们将参数空间的坐标表示为极坐标下的γ和θ。因为同一条直线上的点对应的(γ,θ)是相同的，因此可以先将图片进行边缘检测，然后对图像上每一个非零像素点，在参数坐标下变换为一条直线，那么在直角坐标下属于同一条直线的点便在参数空间形成多条直线并内交于一点。因此可用该原理进行直线检测。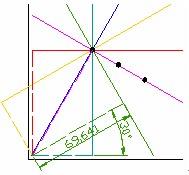

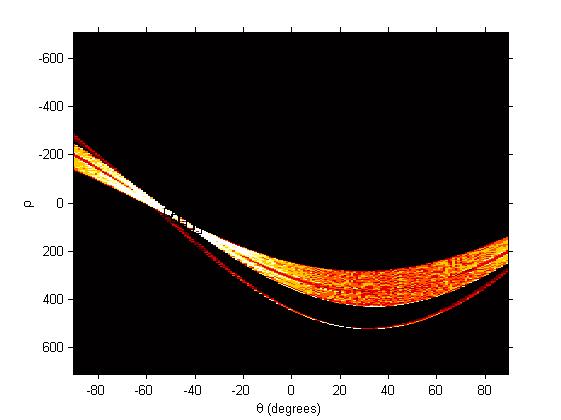
如图 所示，对于原图内任一点(x,y)都可以在参数空间形成一条直线，以图中一条直线为例有参数(γ,θ)=(69.641,30°)，所有属于同一条直线上的点会在参数空间交于一点，该点即为对应直线的参数。由该图中所有直线所得到的(γ,θ)在参数空间中得到一系列对应曲线见图 霍夫统计变换结果。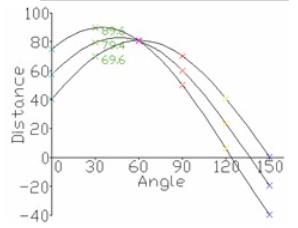

二、源代码

clear all;
close all;
clc;

img= imread('3.jpg');
img= rgb2gray(img);
%% 归一化处理
figure(1);
imshow(mat2gray(img));
hold on;
[M, N] = size(img);
%% 倾斜校正与透视变换
dot=[120,40;401,73;69,309;339,395];
%取四个点，依次是左上，右上，左下，右下,这里我取的是四个角
plot(dot(:,1),dot(:,2),'*');title('经灰度化的原图及其倾斜校正特征点');
w=round(sqrt((dot(1,1)-dot(2,1))^2+(dot(1,2)-dot(2,2))^2));     %从原四边形获得新矩形宽
h=round(sqrt((dot(1,1)-dot(3,1))^2+(dot(1,2)-dot(3,2))^2));     %从原四边形获得新矩形高         round  四舍五入取整

y=[dot(1,1) dot(2,1) dot(3,1) dot(4,1)];        %四个原顶点
x=[dot(1,2) dot(2,2) dot(3,2) dot(4,2)];

%这里是新的顶点，我取的矩形,也可以做成其他的形状
%大可以原图像是矩形，新图像是从dot中取得的点组成的任意四边形
Y=[dot(1,1) dot(1,1) dot(1,1)+h dot(1,1)+h];     
X=[dot(1,2) dot(1,2)+w dot(1,2) dot(1,2)+w];

B=[X(1) Y(1) X(2) Y(2) X(3) Y(3) X(4) Y(4)]';
%变换后的四个顶点，方程右边的值
%联立解方程组，方程的系数
A=[x(1) y(1) 1 0 0 0 -X(1)*x(1) -X(1)*y(1);             
   0 0 0 x(1) y(1) 1 -Y(1)*x(1) -Y(1)*y(1);
   x(2) y(2) 1 0 0 0 -X(2)*x(2) -X(2)*y(2);
   0 0 0 x(2) y(2) 1 -Y(2)*x(2) -Y(2)*y(2);
   x(3) y(3) 1 0 0 0 -X(3)*x(3) -X(3)*y(3);
   0 0 0 x(3) y(3) 1 -Y(3)*x(3) -Y(3)*y(3);
   x(4) y(4) 1 0 0 0 -X(4)*x(4) -X(4)*y(4);
   0 0 0 x(4) y(4) 1 -Y(4)*x(4) -Y(4)*y(4)];

fa=inv(A)*B;        %用四点求得的方程的解，也是全局变换系数  inv  求逆运算
a=fa(1);b=fa(2);c=fa(3);
d=fa(4);e=fa(5);f=fa(6);
g=fa(7);h=fa(8);

rot=[d e f;
     a b c;
     g h 1];        
%公式中第一个数是x,Matlab第一个表示y，所以我矩阵1,2行互换了
 

pix1=rot*[1 1 1]'/(g*1+h*1+1);  %变换后图像左上点
pix2=rot*[1 N 1]'/(g*1+h*N+1);  %变换后图像右上点
pix3=rot*[M 1 1]'/(g*M+h*1+1);  %变换后图像左下点
pix4=rot*[M N 1]'/(g*M+h*N+1);  %变换后图像右下点

height=round(max([pix1(1) pix2(1) pix3(1) pix4(1)])-min([pix1(1) pix2(1) pix3(1) pix4(1)]));     %变换后图像的高度
width=round(max([pix1(2) pix2(2) pix3(2) pix4(2)])-min([pix1(2) pix2(2) pix3(2) pix4(2)]));      %变换后图像的宽度
imgn=zeros(height,width);
img_mask=zeros(height,width);

if min([pix1(1) pix2(1) pix3(1) pix4(1)]) >= 0
    delta_y = -round(abs(min([pix1(1) pix2(1) pix3(1) pix4(1)])));
else
    delta_y = round(abs(min([pix1(1) pix2(1) pix3(1) pix4(1)])));            %取得y方向的负轴超出的偏移量
end;
if min([pix1(2) pix2(2) pix3(2) pix4(2)]) >= 0
    delta_x = -round(abs(min([pix1(2) pix2(2) pix3(2) pix4(2)])));
else
    delta_x = round(abs(min([pix1(2) pix2(2) pix3(2) pix4(2)])));            %取得x方向的负轴超出的偏移量
end;                                                                      
inv_rot=inv(rot);

for i = 1-delta_y:height-delta_y                        %从变换图像中反向寻找原图像的点，以免出现空洞，和旋转放大原理一样
    for j = 1-delta_x:width-delta_x
        pix=inv_rot*[i j 1]';       %求原图像中坐标，因为[YW XW W]=fa*[y x 1],所以这里求的是[YW XW W],W=gy+hx+1;
        pix=inv([g*pix(1)-1 h*pix(1);g*pix(2) h*pix(2)-1])*[-pix(1) -pix(2)]'; %相当于解[pix(1)*(gy+hx+1) pix(2)*(gy+hx+1)]=[y x],这样一个方程，求y和x，最后pix=[y x];
        
        if pix(1)>=0.5 && pix(2)>=0.5 && pix(1)<=M && pix(2)<=N
            imgn(i+delta_y,j+delta_x)=img(round(pix(1)),round(pix(2)));     %最邻近插值,也可以用双线性或双立方插值
            img_mask(i+delta_y,j+delta_x)=1;
        end  
    end
end
 
%% 显示并以文件格式保存图像
figure(2);imshow(uint8(imgn));title('倾斜校正后的图像');
print(gcf,'-djpeg','abc.jpeg');
hold on;

%% 霍夫变换，同基础算法，清除相关变量
clearvars -except imgn img_mask
I = uint8(imgn);

hgram = 225: -1 :15;
I = histeq(I, hgram);
figure(3), imshow(I, []); title('直方图规定化');
hold on;

rotI= medfilt2(I,[3 3]); %3x3矩阵的中值滤波
figure(4), imshow(rotI, []); title('中值滤波');
hold on ;
 
%% 边缘检测
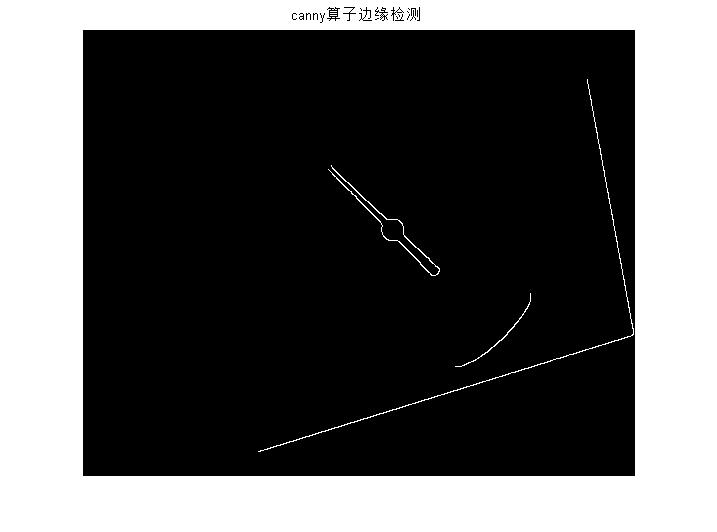
BW0 = edge(rotI,'canny',0.8);
figure(5), imshow(BW0);title('canny算子边缘检测');
hold on ;

se1=strel('disk',50);  %创建一个半径为50的平坦型圆盘结构元素
img_mask = imerode(img_mask,se1);
BW = BW0&img_mask;  %滤除边界
%% 霍夫变换检测直线
[H,T,R] = hough(BW);
figure(6),imshow(imadjust(mat2gray(H)),[],'XData',T,'YData',R,'InitialMagnification','fit');
xlabel('\\theta (degrees)'), ylabel('\\rho');
axis on, axis normal, hold on;
colormap(hot)
P  = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
x = T(P(:,2)); y = R(P(:,1));
plot(x,y,'s','color','black');
lines = houghlines(BW,T,R,P,'FillGap',52,'MinLength',35);
figure(7), imshow(uint8(imgn)),title('霍夫变换提取的直线'); hold on


%  提取指针直线
for  k = 1: length(lines)
   xy = [lines(k).point1; lines(k).point2];
   plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
 
   % Plot beginnings and ends of lines
   plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
   plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
 
end

 %% 读数

三、运行结果

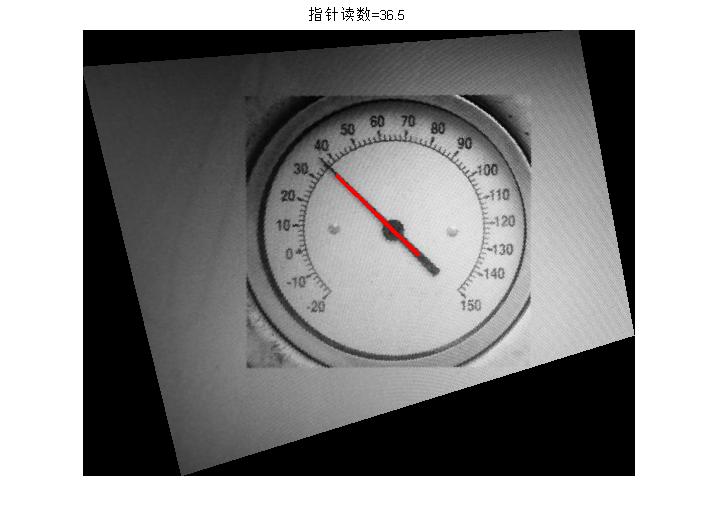
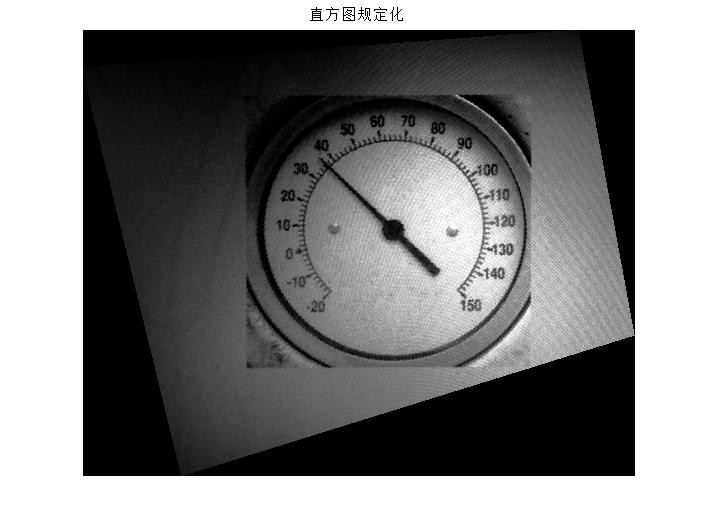
四、备注

代码下载https://www.cnblogs.com/matlabxiao/p/14883637.html