机器学习- 吴恩达Andrew Ng Week7 知识总结Support Vector Machines

Posted 2021-06-30 架构师易筋

Coursera课程地址

因为Coursera的课程还有考试和论坛，后续的笔记是基于Coursera
https://www.coursera.org/learn/machine-learning/home/welcome

Support Vector Machines 支持向量机

1. Optimization Objective 优化目标

在支持向量机（SVM）是另一种类型的监督机器学习算法。它有时更干净、更强大。

回想一下，在逻辑回归中，我们使用以下规则：

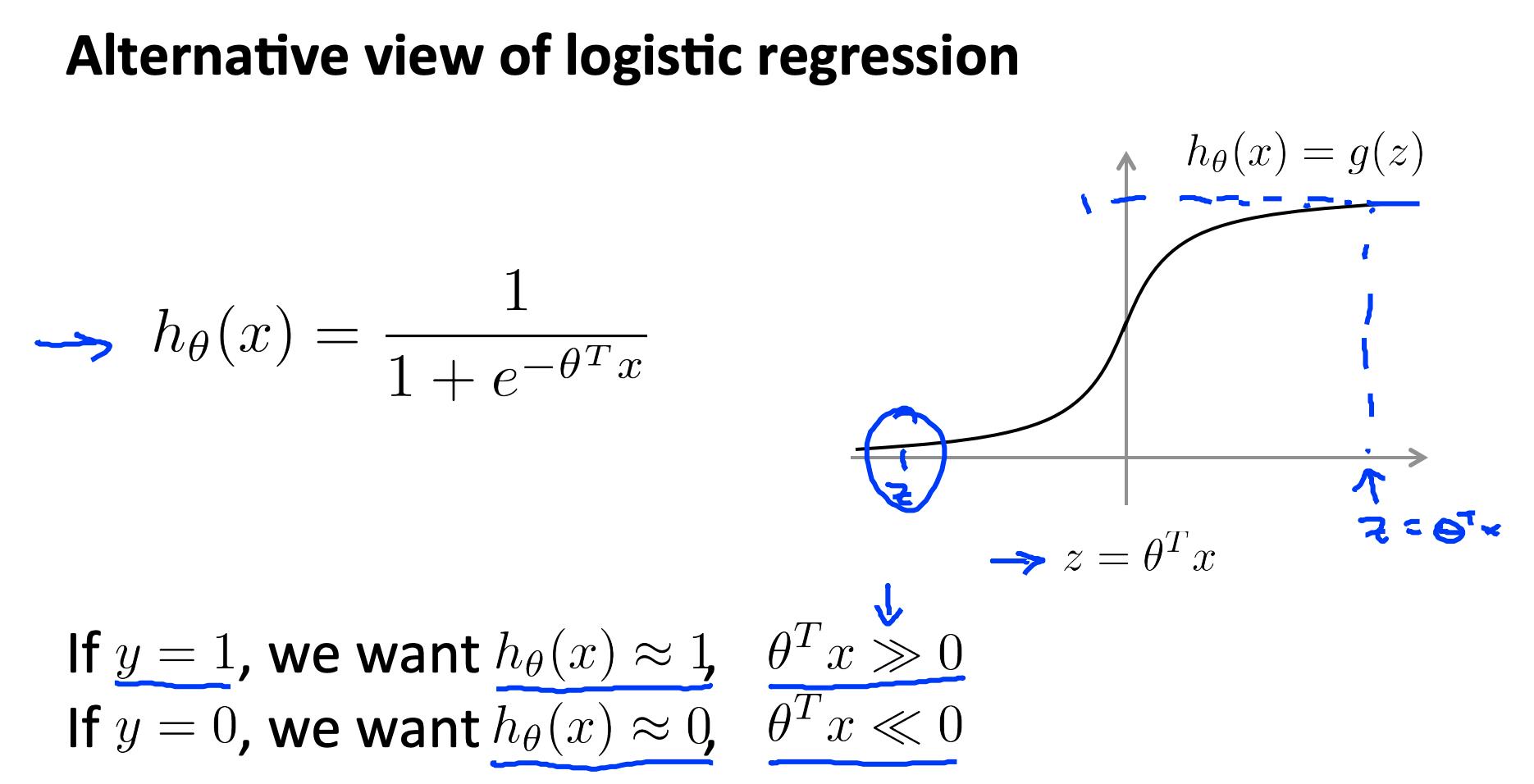
• 如果y=1，那么
  

• 如果 y=0，则
  

回想一下（非正则化）逻辑回归的成本函数：

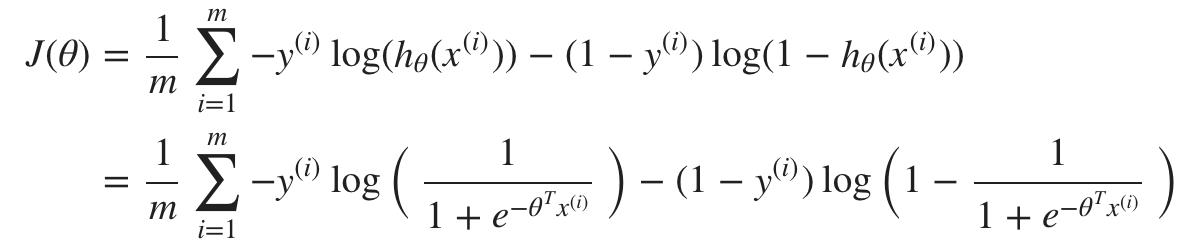
为了制作支持向量机，我们将修改成本函数的第一项

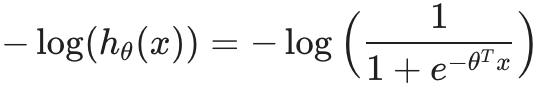
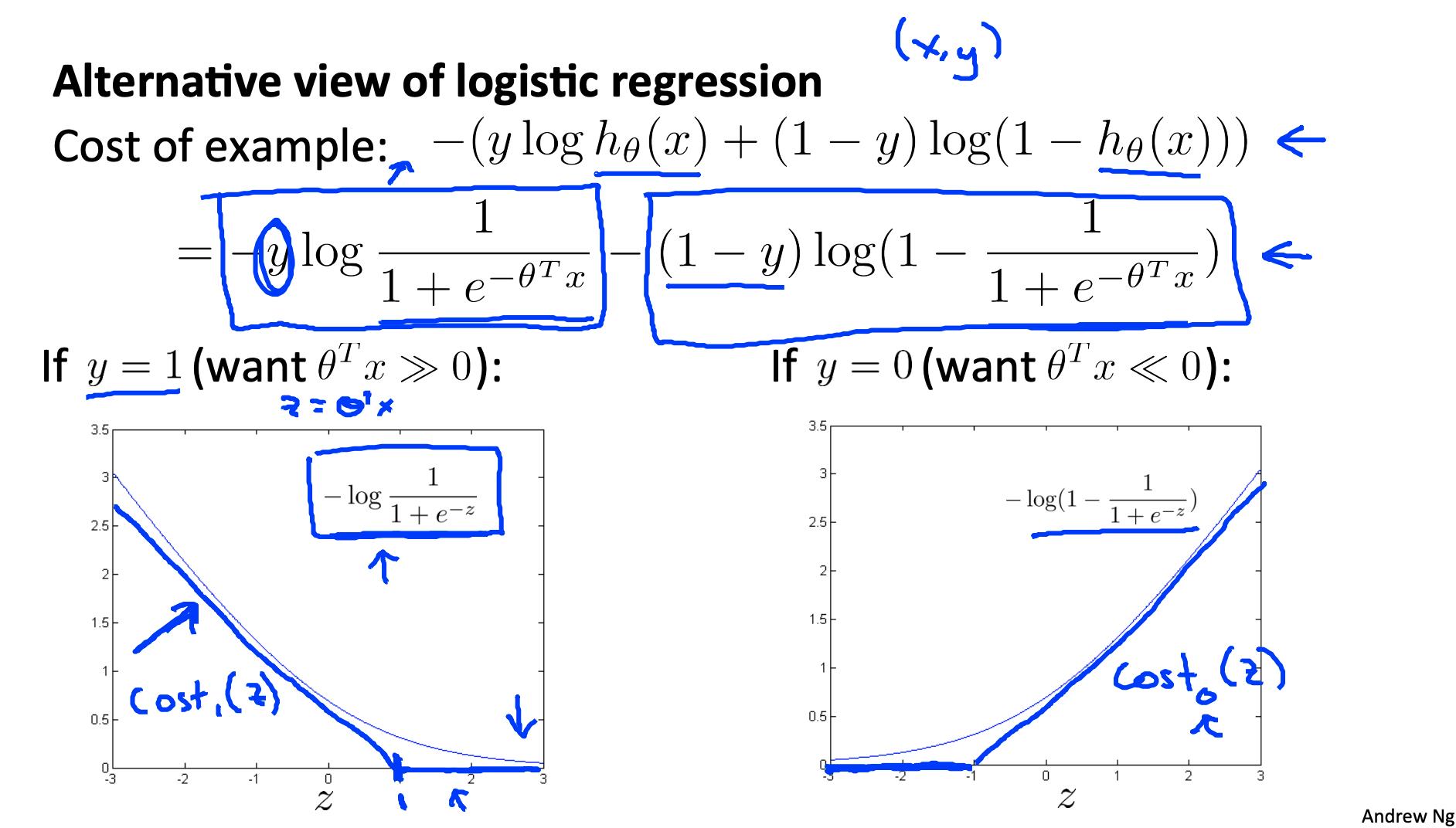
θ(T)x (从现在开始，我们将把它称为 z) 大于1，它输出 0。此外，对于 z 小于 1 的值，我们将使用直线下降线而不是 sigmoid 曲线。（在文献中，这称为铰链损失（https://en.wikipedia.org/wiki/Hinge_loss))）函数。）

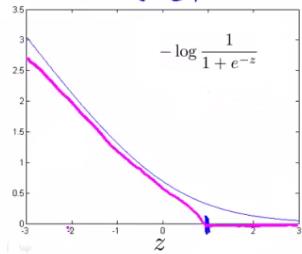
同样，我们修改成本函数的第二项

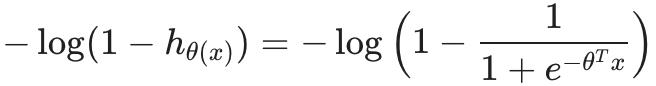
所以当 z小于-1 时，它输出 0。我们还修改它，以便对于大于 -1 的 z 值，我们使用直线增加线而不是 sigmoid 曲线。

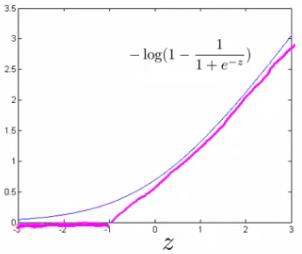
我们将这些表示为cost1(z) 和 cost0(z) （分别注意， cost1(z) 是当 y=1 时的分类成本，并且 cost0(z) 是当 y=0 时的分类成本），我们可以将它们定义如下（其中 k 是定义直线斜率大小的任意常数）：

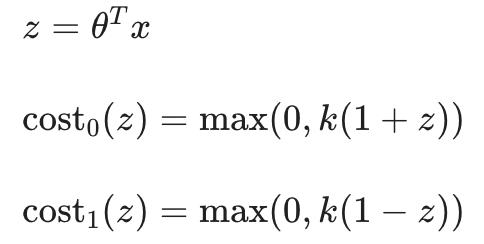
回忆一下（正则化）逻辑回归中的完整成本函数：

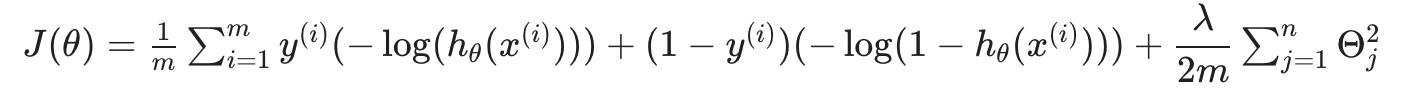
请注意，负号已分配到上述等式中的总和中。

我们可以通过代入将其转化为支持向量机的成本函数cost0(z) 和 cost1(z) :

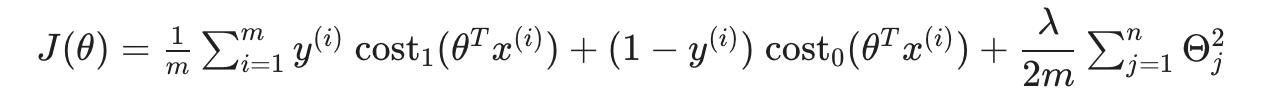
我们可以通过将其乘以 m 来优化它（从而去除分母中的 m 因子）。请注意，这不会影响我们的优化，因为我们只是将成本函数乘以一个正常数（例如，minimizing (u-5)^2 + 1 给我们 5；乘以 10 使其成为10(u-5)^2 + 10 最小化时仍然给我们 5）。

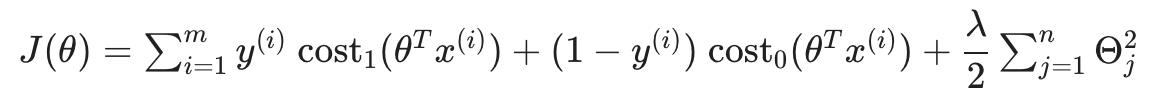
此外，约定要求我们使用因子 C 而不是 λ 进行正则化，如下所示：

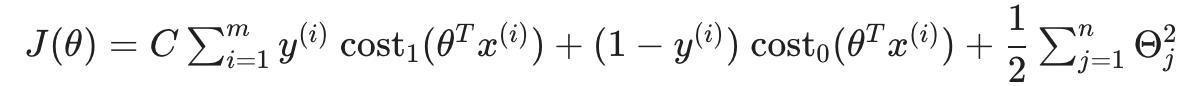
这相当于将方程乘以 C = 1 / λ ，因此在优化时会产生相同的值。现在，当我们希望更多地正则化（即减少过拟合）时，我们减小C，而当我们希望更少地正则化（即减少欠拟合）时，我们增加C。

最后，请注意支持向量机的假设不被解释为 y 为 1 或 0 的概率（就像逻辑回归假设一样）。相反，它输出 1 或 0。（用技术术语来说，它是一个判别函数。）

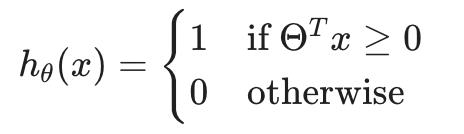
2. 大边距直觉 Large Margin Intuition

考虑支持向量机的一种有用方法是将它们视为大边距分类器。

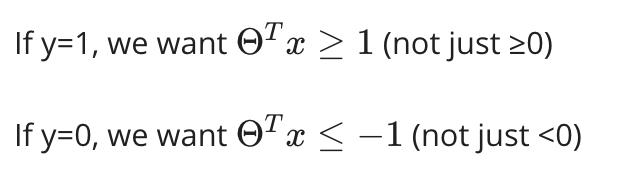
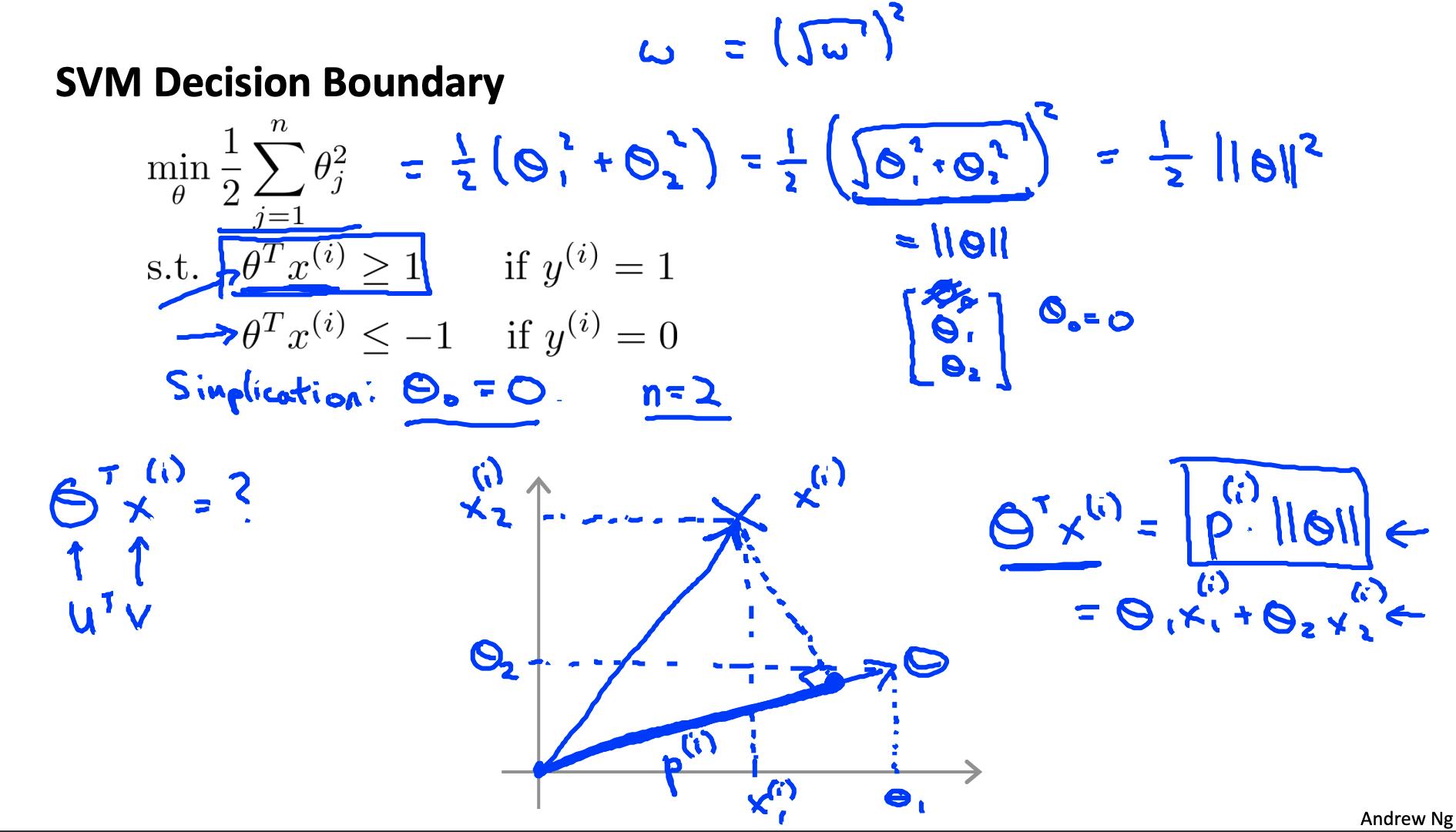
现在，当我们将常数 C 设置为一个非常大的值（例如 100,000）时，我们的优化函数将约束 Θ，使得方程 A（每个示例的成本总和）等于 0。我们对 Θ 施加以下约束：

如果 C 非常大，我们必须选择 Θ 参数使得：

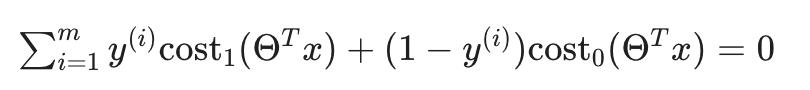
这将我们的成本函数减少为：

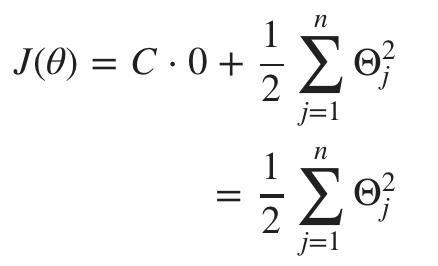
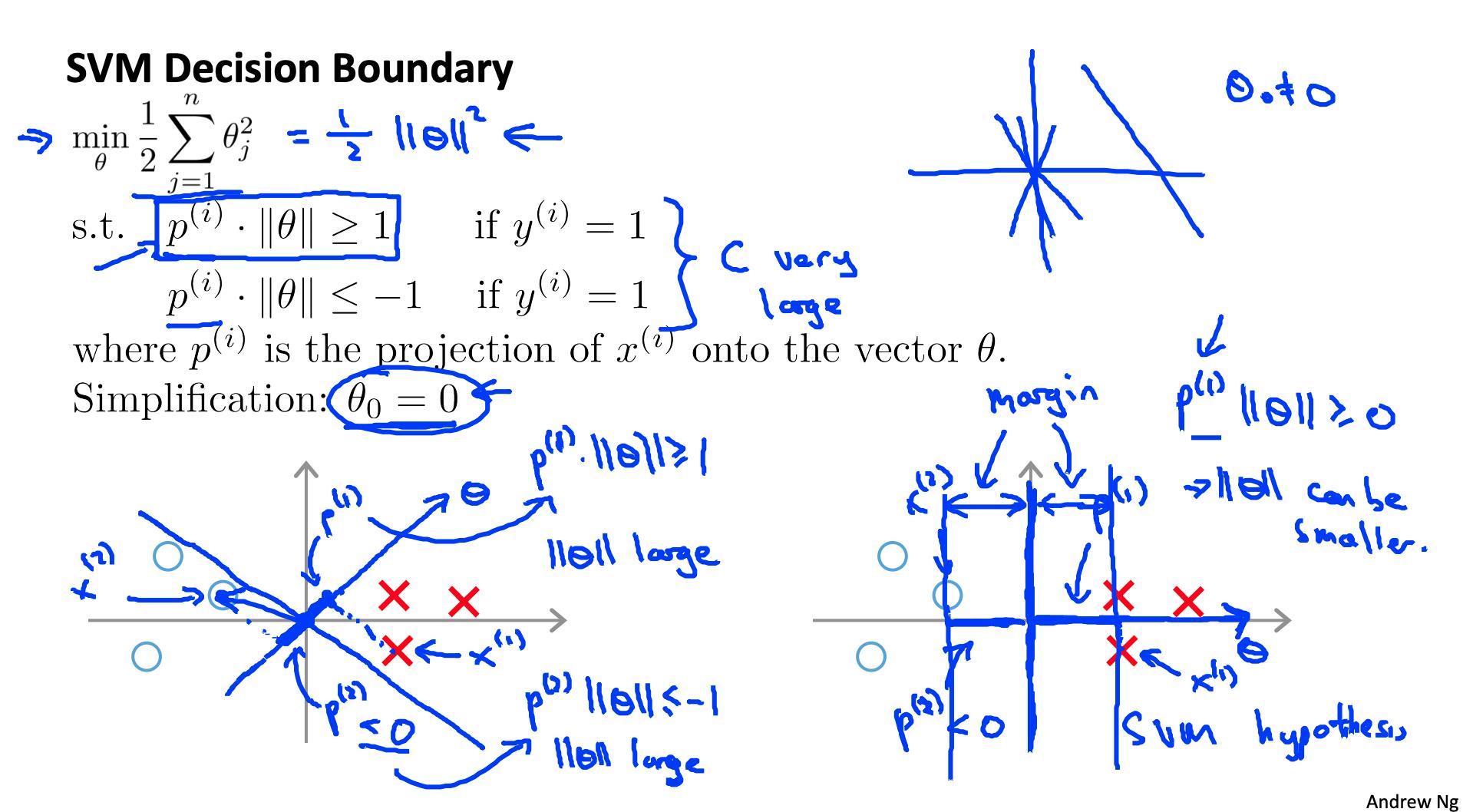
回想一下逻辑回归中的决策边界（分隔正例和负例的线）。在 SVM 中，决策边界具有一个特殊的特性，即它尽可能远离正例和反例。

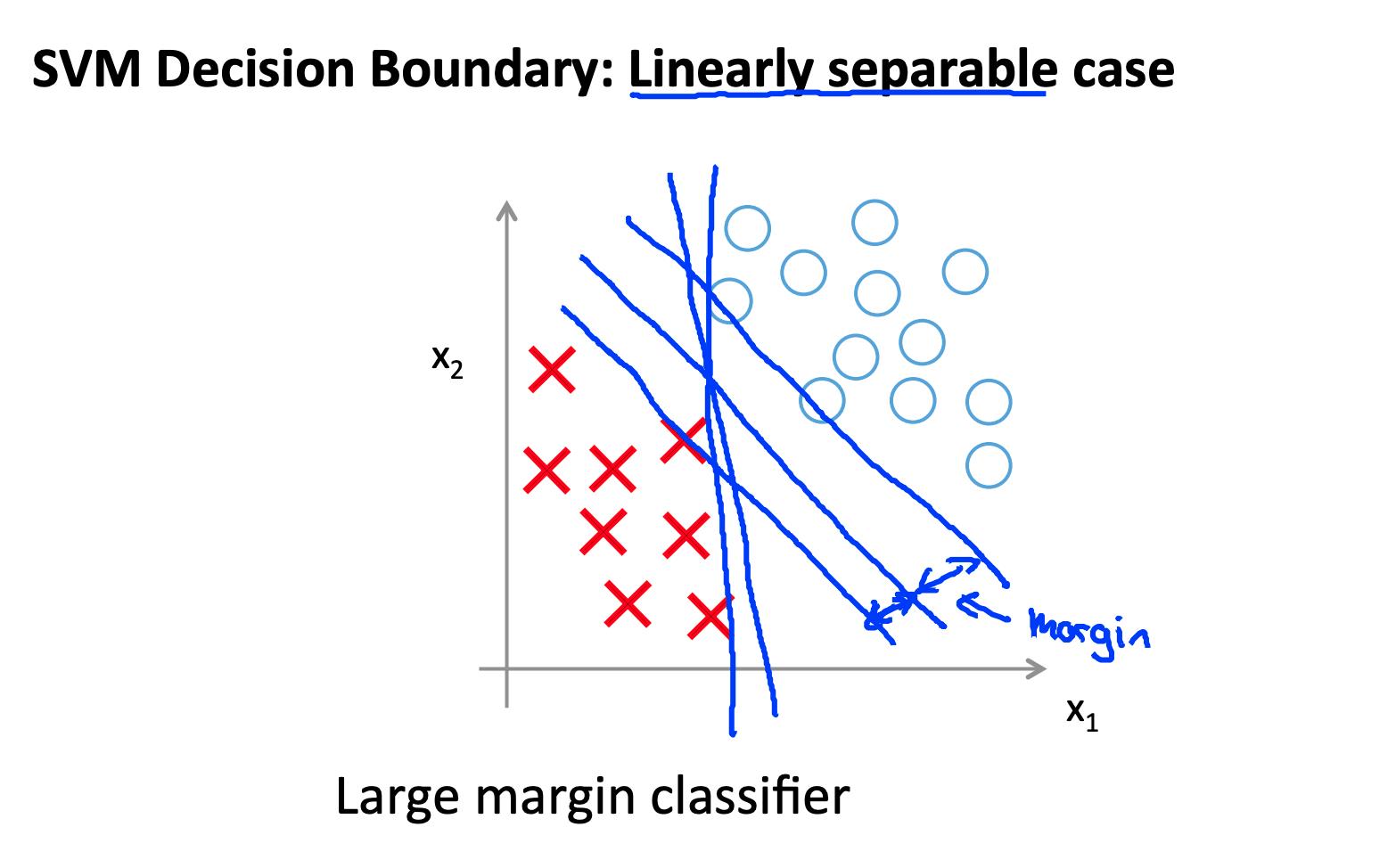
决策边界到最近示例的距离称为边距。由于 SVM 最大化了这个裕度，所以它通常被称为大裕度分类器。

SVM 将负例和正例分开很大。

只有在C 非常大时才能实现如此大的裕度。

当一条直线可以将正例和负例分开时，数据是线性可分的。

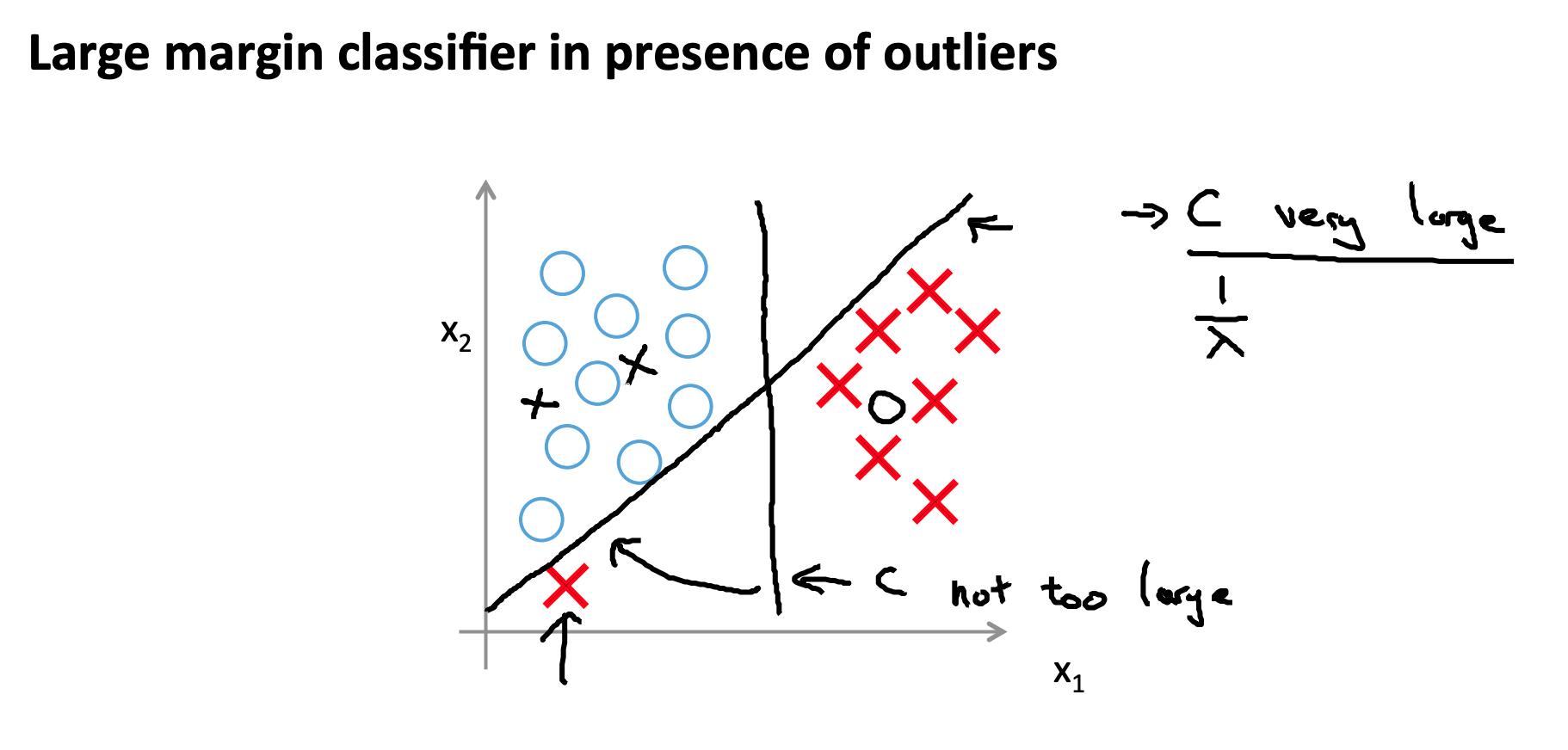
如果我们有不想影响决策边界的异常样本，那么我们可以减少C。

增加和减少C类似于分别减少和增加λ，可以简化我们的决策边界。

3. 大边距分类背后的数学（可选）Mathematics Behind Large Margin Classification (Optional)

矢量内积
假设我们有两个向量，u 和 v：

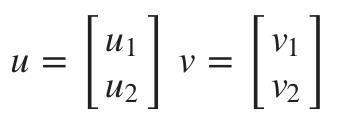
向量 v的长度表示为||v||，它描述了图上从原点 (0,0) 到 (v1,v2)

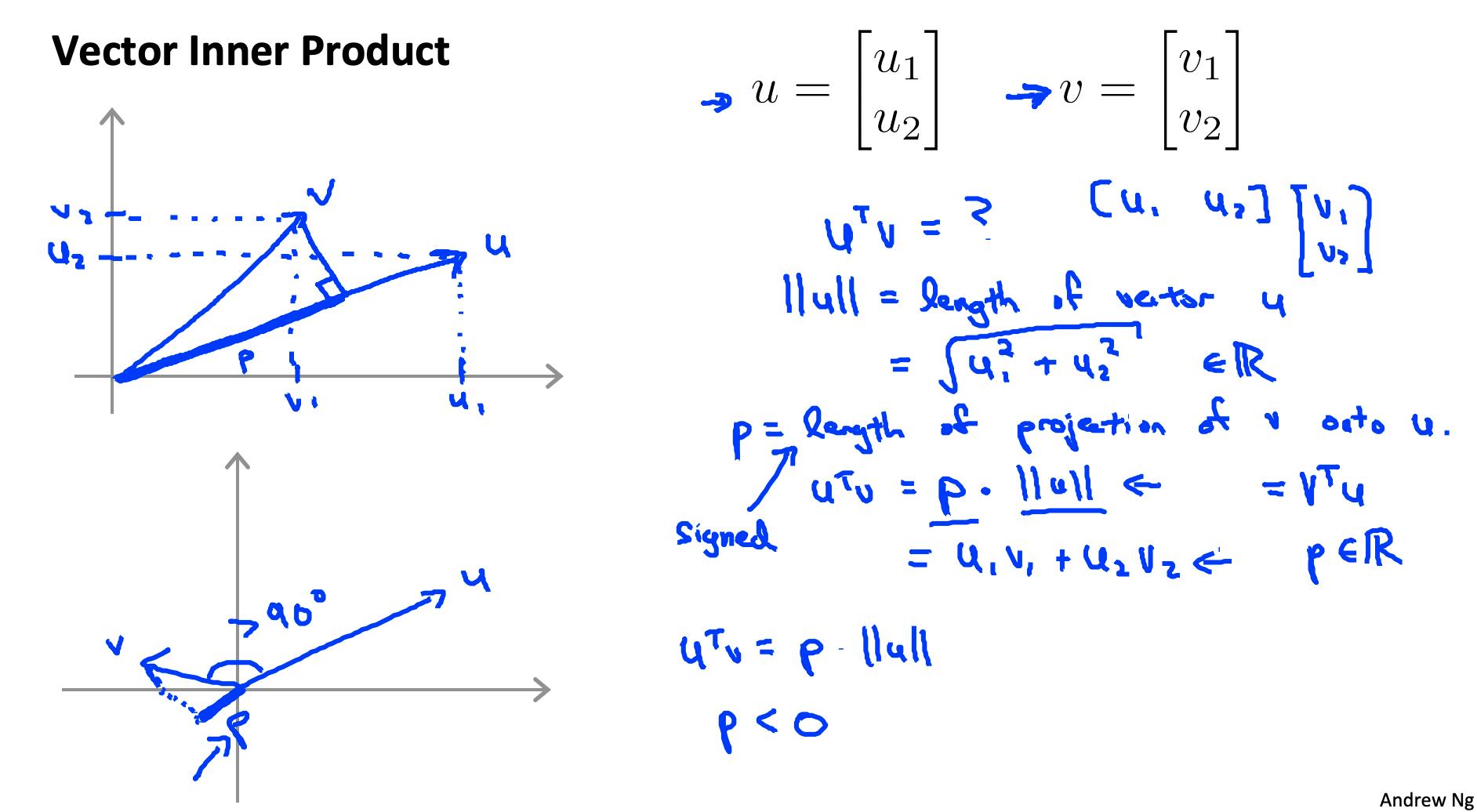
向量 v 的长度可以计算为

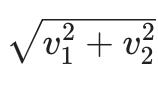
根据勾股定理。

向量 v 到向量 u的投影是通过从 u 到 v 的末端取直角，创建一个直角三角形来找到的。

如果v 和 u 的线之间的角度大于 90 度，则投影 p 将为负。

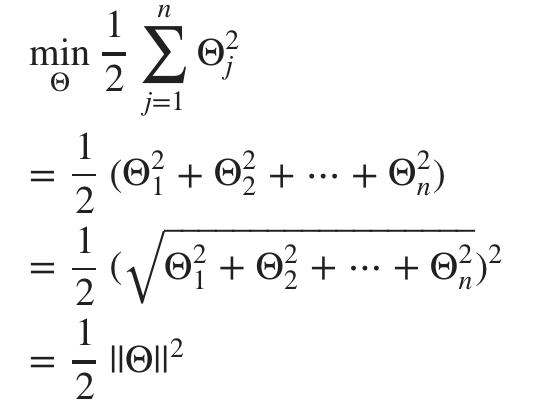
4. 内核 I

内核允许我们使用支持向量机制作复杂的非线性分类器。

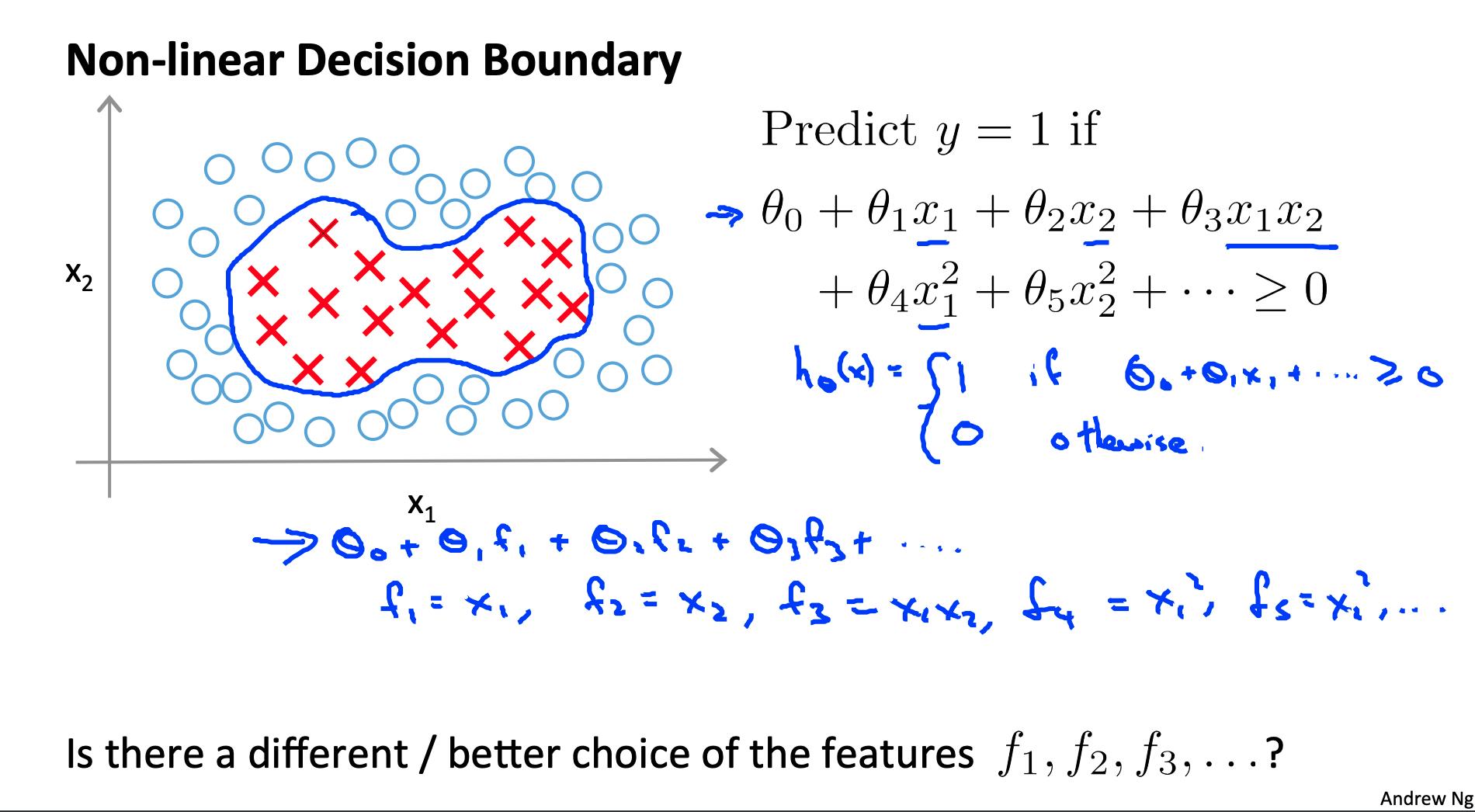
给定 x，根据与地标的接近程度计算新特征 L(1), L(2), L(3).
为此，我们找到 x 和某个地标的“相似性” L(i).

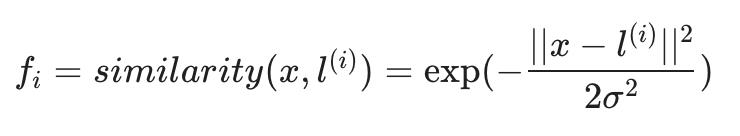
这种“相似性”函数称为Gaussian Kernel高斯内核。它是内核的一个具体示例。

相似度函数也可以写成：

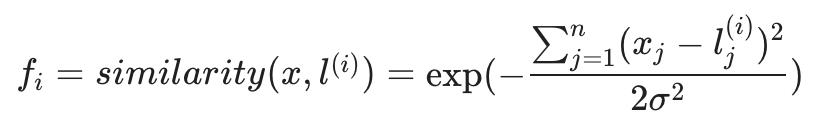
相似度函数有几个属性

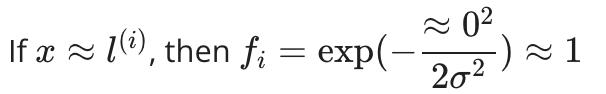
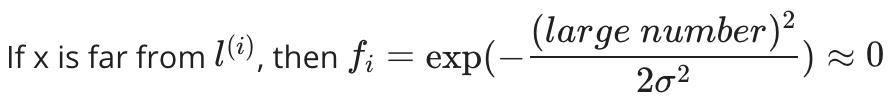
换句话说，如果 x 和地标相近，那么相似度就会接近 1，如果 x 和地标相距很远，那么相似度就会接近于 0。

每个地标都为我们提供了假设中的特征：

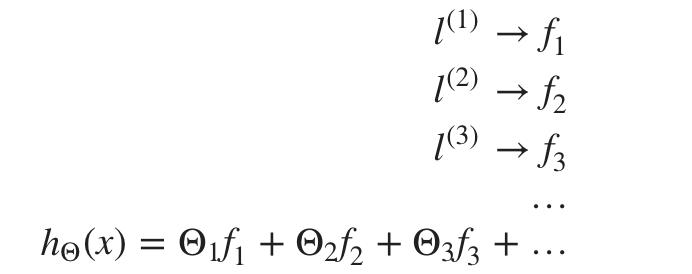
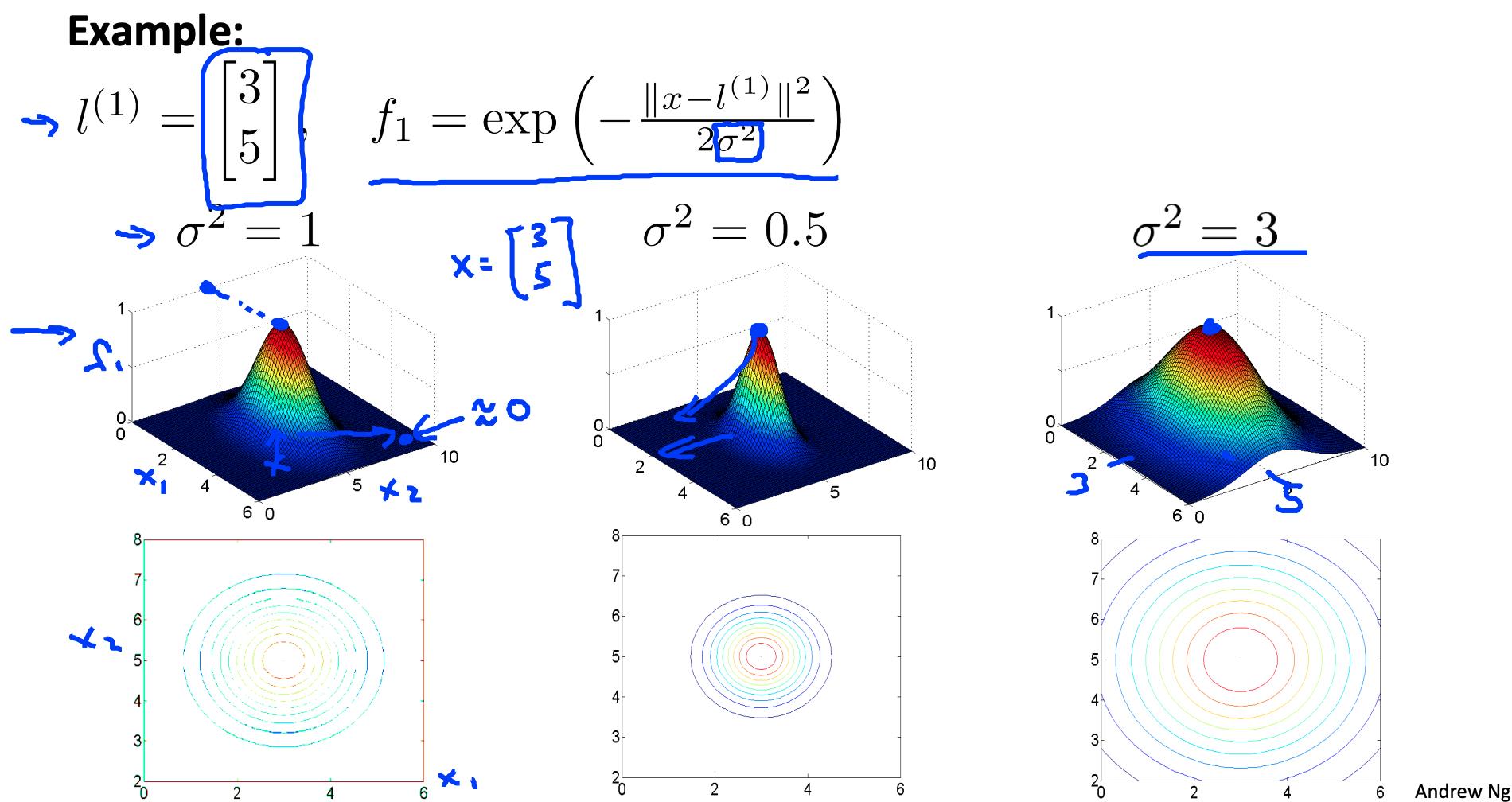
σ^2是高斯核的一个参数，可以修改它来增加或减少我们特征的下降f(i). 结合查看 Θ 内部的值，我们可以选择这些地标来获得决策边界的大致形状。

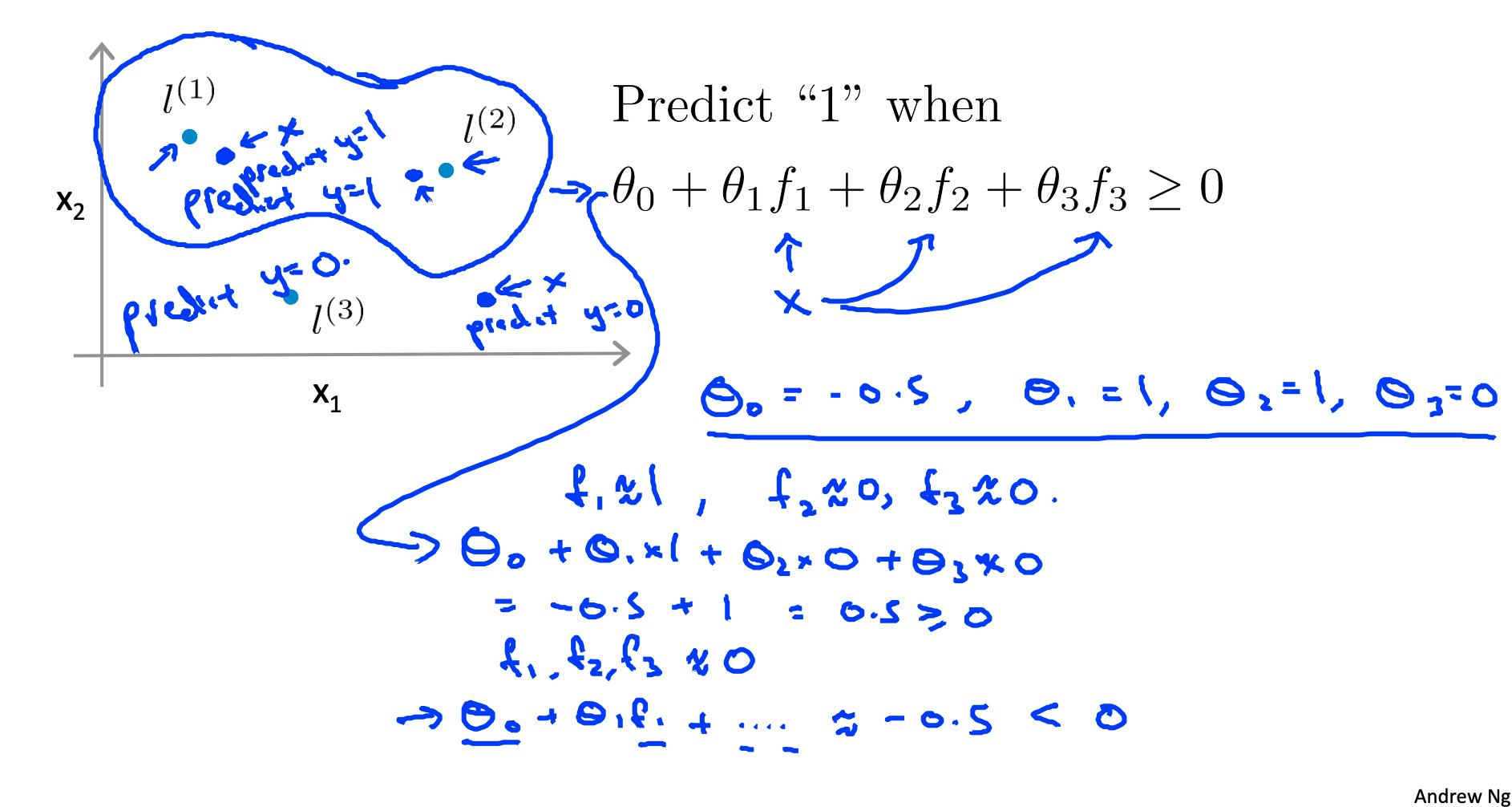
5. 内核II

获取地标的一种方法是将它们放在与所有训练示例完全相同的位置。这为我们提供了 m 个地标，每个训练示例有一个地标。

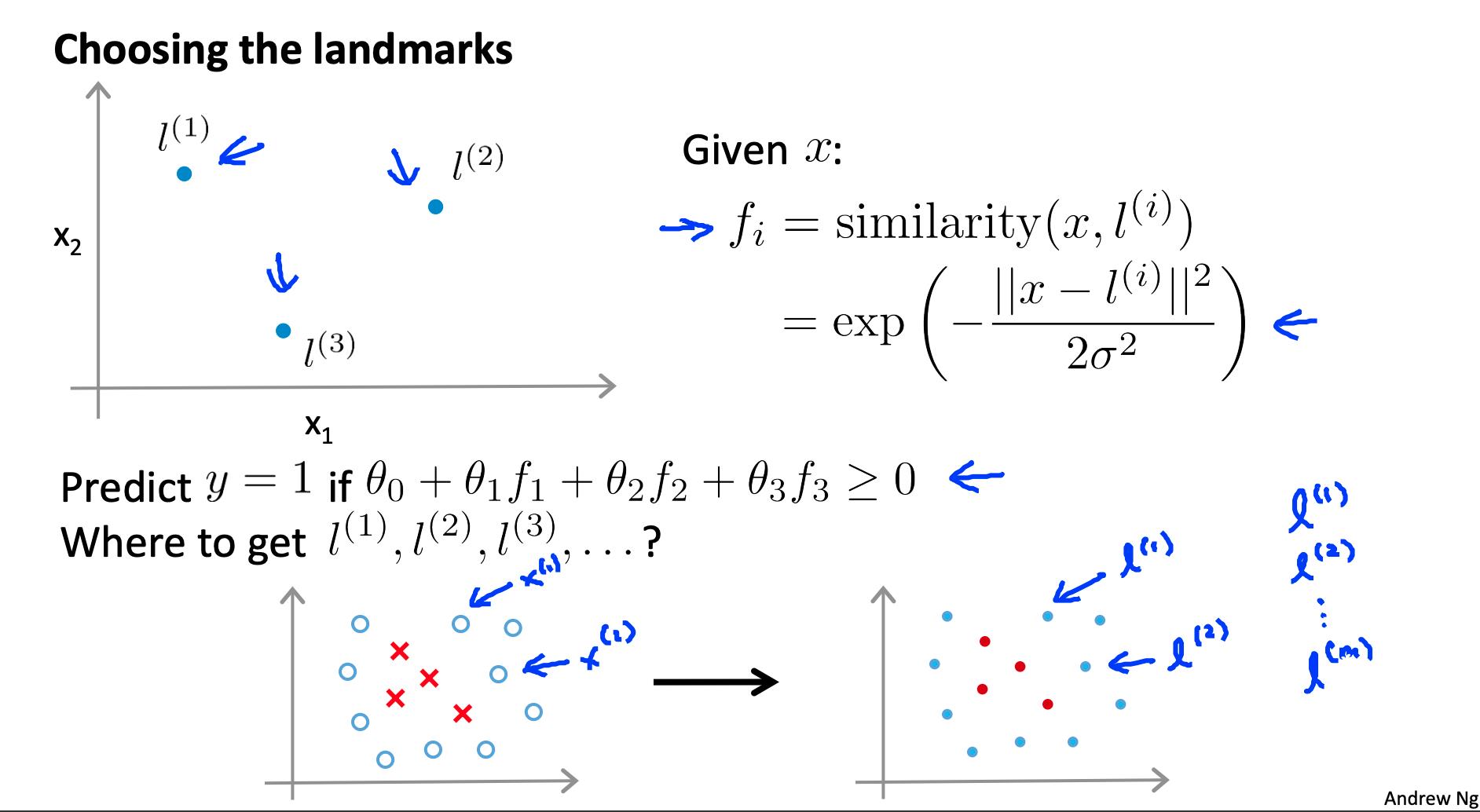
给定示例 x：

使用内核生成 f(i) 不仅限于 SVM，也可以应用于逻辑回归。然而，由于 SVM 上的计算优化，内核与 SVM 结合比其他算法快得多，因此几乎总是发现内核仅与 SVM 结合。

5.1 选择 SVM 参数

选择 C（回想一下 C = 1 / λ

• 如果 C 很大，那么我们会得到更高的方差/更低的偏差
• 如果 C 很小，那么我们会得到较低的方差/较高的偏差
  我们必须选择的另一个参数是 σ^2 从高斯核函数：

带着大 σ^2 ，特征 fi 变化更平滑，导致更高的偏差和更低的方差。

带着小 σ^2，特征 fi 变化不太平滑，导致较低的偏差和较高的方差。

6. 使用 SVM

已经编写了很多好的 SVM 库。A. Ng 经常使用“liblinear”和“libsvm”。在实际应用中，您应该使用这些库之一，而不是重写函数。

在实际应用中，您需要做出的选择是：

• 参数C的选择
• 核的选择（相似函数）
• 无核（“线性”核）——给出标准的线性分类器
• 当 n 大时选择 m 小时
• Gaussian Kernel（上）——需要选择 σ^2
• 当 n 较小且 m 较大时选择

该库可能会要求您提供内核函数。

注意：在使用高斯核之前一定要进行特征缩放。

注意：并非所有相似度函数都是有效的内核。它们必须满足“Mercer 定理”，以保证 SVM 包的优化正确运行并且不会发散。

您想使用训练和交叉验证数据集训练 C 和核函数的参数。

6.1 多类分类

许多 SVM 库都内置了多类分类。

您可以使用一对多的方法，就像我们对逻辑回归所做的那样，其中y ∈1 、2 、3 、… K with Θ(1) ,Θ(2) ,…,Θ(K)

我们选择最大的类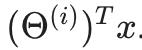

6.2 逻辑回归与 SVM

如果 n 很大（相对于 m），则使用逻辑回归或没有内核的 SVM（“线性内核”）

如果 n 很小而 m 是中间值，则使用带有高斯核的 SVM

如果 n 小而 m 大，则手动创建/添加更多特征，然后使用逻辑回归或没有内核的 SVM。

在第一种情况下，我们没有足够的例子来需要复杂的多项式假设。在第二个例子中，我们有足够多的例子，我们可能需要一个复杂的非线性假设。在最后一种情况下，我们希望增加我们的特征，以便逻辑回归变得适用。

注意：神经网络可能适用于任何这些情况，但训练速度可能较慢。

6.3 其他参考

“支持向量机的白痴指南”：http://web.mit.edu/6.034/wwwbob/svm-notes-long-08.pdf

参考

https://www.coursera.org/learn/machine-learning/resources/Es9Qo

https://www.coursera.org/learn/machine-learning/supplement/pSe2X/lecture-slides