LeetCode 149. 直线上最多的点数 / NC14 二叉树的之字形层序遍历 / NC37 合并区间

Posted 2021-06-30 Zephyr丶J

149. 直线上最多的点数

2021.6.24每日一题

题目描述

给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。


示例 1：

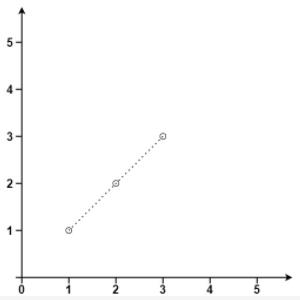
输入：points = [[1,1],[2,2],[3,3]]
输出：3
示例 2：

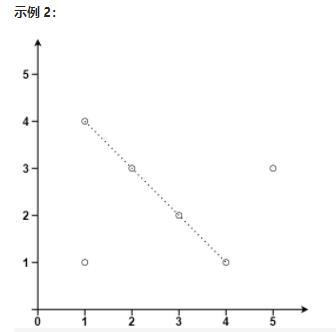
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/max-points-on-a-line
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

两点确定一条直线，然后去遍历第三个点，看是否在这条直线上
因为点的个数小于等于300，所以O(n^3)能过应该
需要注意计算斜率的时候，会出现除数为0的情况，要特别考虑
另外计算斜率的时候，整数相除不会得出一个浮点数，因此要用double类型
提交超过80%，哇，困难题做出来心情舒畅

class Solution {
    public int maxPoints(int[][] points) {
        //两个点可以确定一条直线，要判断有几个点在一条直线上，需要一个一个遍历吧
        //枚举点，和另一个点组成一条直线，然后判断其他点是否在这个直线上,复杂度在10^7次左右
        //
        int res = 0;
        int max = 2;
        int l = points.length;
        if(l == 1)
            return 1;
        for(int i = 0; i < l - 1; i++){
            for(int j = i + 1; j < l; j++){
                int[] p1 = points[i];
                int[] p2 = points[j];
                double k = 0.0;
                if(p2[0] - p1[0] != 0)
                    k = (p2[1] - p1[1]) * 1.0 / (p2[0] - p1[0]);
                else
                    k = Double.MAX_VALUE;
                
                for(int t = j + 1; t < l; t++){
                    double k2 = 0.0;
                    if(points[t][0] - p1[0] != 0)
                        k2 = (points[t][1] - p1[1]) * 1.0 / (points[t][0] - p1[0]);
                    else
                        k2 = Double.MAX_VALUE;
                    if(k == k2)
                        max++;
                }
                res = Math.max(max, res);
                max = 2;
            }
        }
        return res;
    }
}

看了零神的官解，感觉自己其实做了个寂寞。可能最多当个中等题来做了
这里有个关键点，就是如果浮点型精度不够的话，需要换一种方法来统计斜率。
也就是用一个二元数组，将斜率的分子分母分别记录，但是可能出现1/2 和 2/4 这种情况，因此需要除以分子分母的最大公因数
还有就是-1 / 2 和 1 / -2 这种情况，因此需要统一一下，让分子或者分母不可能为负数
如果分子为0或者分母为0的时候，无法求最大公因数，因此需要特殊处理
另外，根据横纵坐标的取值范围，可以得到将二元组用一个数来表示，也就是 val = my + (2 * 10 ^ 4 + 1) * mx

找最大公因数，辗转相除法，学习一下，忘了
两个整数的最大公约数等于其中较小的数和两数的相除余数的最大公约数。

class Solution {
    public int maxPoints(int[][] points) {
        //官解方法
        //这里有个关键点，就是如果浮点型精度不够的话，需要换一种方法来统计斜率。
        //也就是用一个二元数组，将斜率的分子分母分别记录，但是可能出现1/2 和 2/4 这种情况，因此需要除以分子分母的最大公因数
        //还有就是-1 / 2 和 1 / -2 这种情况，因此需要统一一下，让分子或者分母不可能为负数
        //如果分子为0或者分母为0的时候，无法求最大公因数，因此需要特殊处理
        //另外，根据横纵坐标的取值范围，可以得到将二元组用一个数来表示，也就是 val  = my + (2 * 10 ^ 4 + 1) * mx
        int res = 0;
        int max = 2;
        int l = points.length;
        if(l <= 2)
            return l;

        for(int i = 0; i < l - 1; i++){
            //当我们找到一条直线经过了图中超过半数的点时，我们即可以确定该直线即为经过最多点的直线
            //当遍历到i时，此时经过点i的直线，最多的点数为l - i，所以如果此时最大值max比l-i大了，就不用遍历了
            if(res > l / 2 || res >= l - i)
                break;
            Map<Integer, Integer> map = new HashMap<>();
            for(int j = i + 1; j < l; j++){
                int x = points[j][0] - points[i][0];
                int y = points[j][1] - points[i][1];
                //特殊处理，不可能分子分母都为0
                if(x == 0)
                    y = 1;
                else if(y == 0)
                    x = 1;
                else{
                    if(y < 0){
                        x = -x;
                        y = -y;
                    }
                    //求最大公约数
                    int gcdXY = gcd(Math.abs(x), Math.abs(y));
                    x /= gcdXY;
                    y /= gcdXY;
                }
                int val = y + x * 20001;
                map.put(val, map.getOrDefault(val, 0) + 1);
            }
            //遍历这个点的结果集

            for(Map.Entry<Integer, Integer> entry : map.entrySet()){
                res = Math.max(entry.getValue() + 1, res);
            }
        }
        return res;
    }
    //找两个数的最大公因数
    //怎么找呢，就是一直找y 和 x % y 的最大公因数，如果 x % y == 0了。那么就说明可以除尽了，输出此时这个数，就是最大公因数
    public int gcd(int x, int y){
        return y == 0 ? x : gcd(y, x % y);
    }
}

三叶姐的暴力解，精度问题处理很巧妙，用的乘法，原理就是如果y1 / x1 = y2 / x2，那么 x1 * y2 = y1 * x2 ，直接超过97…

class Solution {
    public int maxPoints(int[][] ps) {
        int n = ps.length;
        int ans = 1;
        for (int i = 0; i < n; i++) {
            int[] x = ps[i];
            for (int j = i + 1; j < n; j++) {
                int[] y = ps[j];
                int cnt = 2;
                for (int k = j + 1; k < n; k++) {
                    int[] p = ps[k];
                    int s1 = (y[1] - x[1]) * (p[0] - y[0]);
                    int s2 = (p[1] - y[1]) * (y[0] - x[0]);
                    if (s1 == s2) cnt++;
                }
                ans = Math.max(ans, cnt);
            }
        }
        return ans;
    }
}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/max-points-on-a-line/solution/gong-shui-san-xie-liang-chong-mei-ju-zhi-u44s/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

三叶姐的哈希表，键是用字符串存储的，并且没有处理特殊情况，只计算了最大公因数
想了一下，确实也可行，只不过需要理解一会

class Solution {
    public int maxPoints(int[][] ps) {
        int n = ps.length;
        int ans = 1;
        for (int i = 0; i < n; i++) {
            Map<String, Integer> map = new HashMap<>();
            // 由当前点 i 发出的直线所经过的最多点数量
            int max = 0;
            for (int j = i + 1; j < n; j++) {
                int x1 = ps[i][0], y1 = ps[i][1], x2 = ps[j][0], y2 = ps[j][1];
                int a = x1 - x2, b = y1 - y2;
                //这里如果是2 -1 或者 -2 1，最大公约数算出来分别是-1 1，最后除以最大公约数以后还是一样的
                int k = gcd(a, b);
                //用字符串存储
                String key = (a / k) + "_" + (b / k);
                map.put(key, map.getOrDefault(key, 0) + 1);
                //每次都更新，避免了最后的遍历
                max = Math.max(max, map.get(key));
            }
            //加上当前点
            ans = Math.max(ans, max + 1);
        }
        return ans;
    }
    int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/max-points-on-a-line/solution/gong-shui-san-xie-liang-chong-mei-ju-zhi-u44s/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

NC14 二叉树的之字形层序遍历

题目描述

给定一个二叉树，返回该二叉树的之字形层序遍历，（第一层从左向右，下一层从右向左，一直这样交替）
例如：
给定的二叉树是{3,9,20,#,#,15,7},

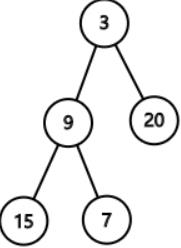
该二叉树之字形层序遍历的结果是
[
[3],
[20,9],
[15,7]
]
示例1
输入：
{1,#,2}

返回值：
[[1],[2]]

思路

又来做这道题了，层序遍历的变种，存储到队列中依然是按层序遍历存储，但是取出来的时候，如果要反方向的话，就反方向插入集合

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 * }
 */

public class Solution {
    /**
     * 
     * @param root TreeNode类 
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> zigzagLevelOrder (TreeNode root) {
        // write code here
        ArrayList<ArrayList<Integer>> res = new ArrayList<>();
        if(root == null)
            return res;
        //双向队列
        Queue<TreeNode> queue = new LinkedList<>();
        boolean order = false; //false从左到右，true从右到左
        queue.offer(root);
        while(!queue.isEmpty()){
            ArrayList<Integer> list = new ArrayList<>();
            int l = queue.size();
            while(l-- > 0){
                //弹出队列元素
                TreeNode node = queue.poll();
                //如果是从左到右，那么按顺序放入list中就行了
                if(!order)
                    list.add(node.val);
                //如果是从右到左，那么按反方向放入list中，也就是每次插入到list的头部
                else
                    list.add(0, node.val);
                
                if(node.left != null)
                    queue.offer(node.left);
                if(node.right != null)
                    queue.offer(node.right);
            }
            order = !order;
            res.add(list);
        }
        return res;
    }
}

NC37 合并区间

题目描述

描述
给出一组区间，请合并所有重叠的区间。
请保证合并后的区间按区间起点升序排列。
示例1
输入：
[[10,30],[20,60],[80,100],[150,180]]

返回值：
[[10,60],[80,100],[150,180]]

思路

记得是刚开始刷题的时候做的一道题，印象还是非常深刻的
给左端点排序，然后根据遍历，将能合并的区间合并，注意遍历到最后要有一次合并

/**
 * Definition for an interval.
 * public class Interval {
 *     int start;
 *     int end;
 *     Interval() { start = 0; end = 0; }
 *     Interval(int s, int e) { start = s; end = e; }
 * }
 */
import java.util.*;
public class Solution {
    public ArrayList<Interval> merge(ArrayList<Interval> intervals) {
        //按区间左端点排序
        Collections.sort(intervals, (a, b) -> (a.start - b.start));
        //排序以后遍历
        ArrayList<Interval> res = new ArrayList<>();
        int l = intervals.size();
        if(l == 0)
            return res;
        int start0 = intervals.get(0).start;
        int end0 = intervals.get(0).end;
        for(int i = 1; i < l; i++){
            int temps = intervals.get(i).start;
            int tempe = intervals.get(i).end;
            if(temps <= end0){
                end0 = Math.max(end0, tempe);
                
            }else{
                res.add(new Interval(start0, end0));
                start0 = temps;
                end0 = tempe;
               
            }
        }
        res.add(new Interval(start0, end0));
        return res;
    }
}