基于匈牙利算法的指派问题优化分析matlab优化算法十二

Posted 2021-06-30 张叔zhangshu

基于匈牙利算法的指派问题优化分析

匈牙利算法

1955年，库恩（ww· Kuhn）提出了匈牙利算法，它是一种关于指派问题的求解方法。匈牙利算法引用了匈牙利数学家康尼格（ D konig）的一个关于矩阵中独立0元素个数的定理：矩阵中独立0元素的个数等于能够覆盖所有0元素的最少直线数匈牙利算法的基本思想是修改效益矩阵的行或列，使得每一行或列中至少有个为零的元素，经过修正后，直至在不同行、不同列中至少有一个零元素，从而得到与这些零元素相对应的一个完全分配方案当它用于效益矩阵时，这个完全分配方案就是一个最优分配，它使总的效益为最小。这种方法总是在有限步内收敛于一个最优解。该方法的理论基础是：在效益矩阵的任何行或列中，加上或减去一个常数后不会改变最优分配。其求解步骤如下第一步，修正效益矩阵，使之变成每一行和每一列至少有一个零元素的缩减矩阵：
（1）从效益矩阵的每一行元素减去各该行中最小元素；
（2）再从所得缩减矩阵的每列减去各该列的最小元素。
第二步，试制一个完全分配方案，它对应于不同行不同列只有一个零元素的缩减矩阵，以求得最优解：
（1）如果得到分布在不同行不同列的N个零元素，那么就完成了求最优解的过程。结束。
（2）如果所分布于不同行不同列中的零元素不够N个，则转下步
第三步，作出覆盖所有零元素的最少数量的直线集合：
（1）标记没有完成分配的行。
（2）标记已标记行上所有未分配零元素所对应的列。
（3）对标记的列中，已完成分配的行进行标记。
（4）重复（2）、（3）直到没有可标记的零元素。
（5）对未标记的行和已标记的列画纵、横线，这就得到能覆盖所有零元素的最少数量的直线集合第四步，修改缩减矩阵，以达到每行每列至少有一个零元素的目的：
（1）在没有直线覆盖的部分中找出最小元素。
（2）对没有画直线的各元素都减去这个元素。
（3）对画了横线和直线交叉处的各元素都加上这个最小元素。
（4）对画了一根直线或横线的各元素保持不变。（5）转第二步。

262匈牙利算法计算实例步骤

以下列矩阵为例：

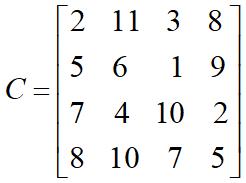
计算步骤如下
（1）先让矩阵C中每行元素减去该行元素中的最小值，再让每列元素减去该列元素中的最小值，这样每行必然会产生至少一个零元素：

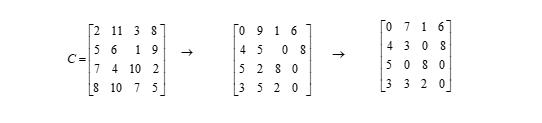
（2）先找出仅有一个“0”元素的行，并划去与该“0”同列的其他“0”元素，然后找出仅有一个“0”元素的列，并划去与该“0”同行的其他“0”元素。

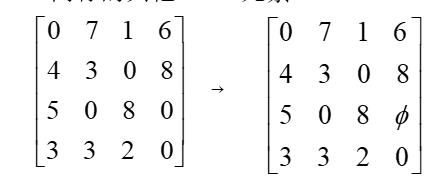
（3）观察矩阵中的零元素的个数是否等于矩阵的阶数，若两者相等则算法结束，否则需要对矩阵进行变化。直到矩阵中零元的个数与矩阵的阶数相等则算法结束。

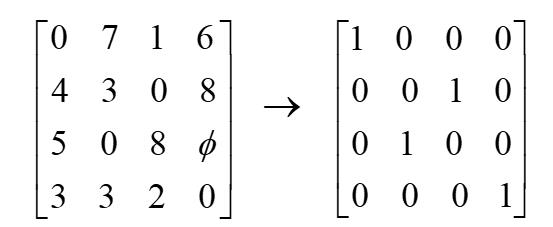
数学模型

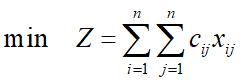
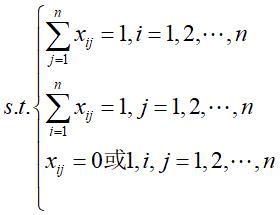
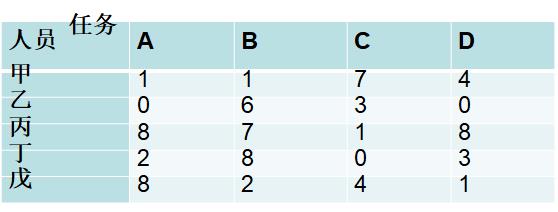
有结果可知，甲做B任务，乙做A任务，丙不做任务，丁做C任务，戊做D任务匈牙利算法对于目标分配是适用的，且仿真速度较快。
代码下载地址