数据结构&算法-图关键路径

Posted 2021-06-30 彩色墨水

图关键路径介绍

AOE网与AOV网都是用来对工程建模的，但它们还是很大的不同，主要体现在AOV网是顶点表示活动的网，它只描述活动之间的制约关系，而AOE网是用边表示活动的网，边上的权值表示活动持续的时间。

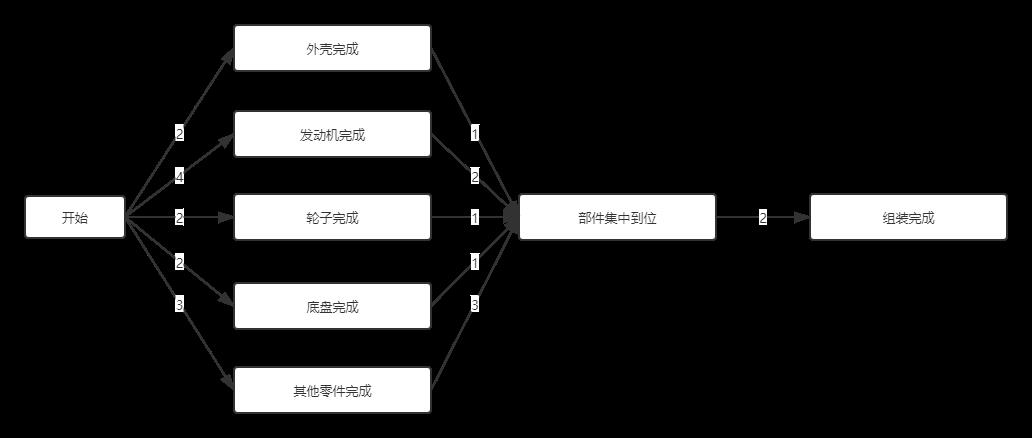
路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。

事件的最早发生时间etv
事件的最晚发生时间ltv
活动的最早开工时间ete
活动的最晚开工时间lte

运行结果

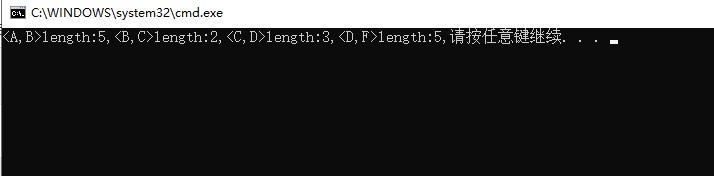
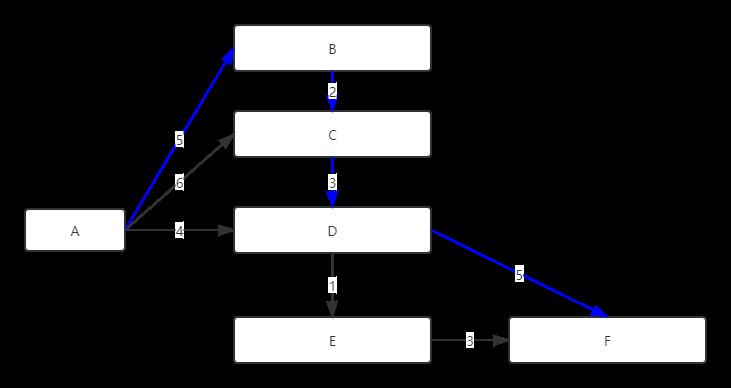
代码

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace CriticalPath
{
    class Program
    {
        static void Main(string[] args)
        {
            OperGL operGL = new OperGL();
            operGL.CreatAlGraph();
            operGL.CriticalPath();
        }

    }

    /// <summary>
    /// 边表结点
    /// </summary>
    class EdgeNode
    {
        /// <summary>
        /// 领接点域，存储该顶点对应的下标
        /// </summary>
        public int adjvex;
        /// <summary>
        /// 用于存储权值，对于非网图可以不需要
        /// </summary>
        public int weight = 0;
        /// <summary>
        /// 链域，指向下一个领接点
        /// </summary>
        public EdgeNode next;

        public EdgeNode(int adjvex, int weight)
        {
            this.adjvex = adjvex;
            this.weight = weight;
        }
        public EdgeNode(int adjvex)
        {
            this.adjvex = adjvex;
        }
    }

    /// <summary>
    /// 顶点表结点
    /// </summary>
    class VertexNode
    {
        /// <summary>
        /// 入度
        /// </summary>
        public int inDeg = 0;
        /// <summary>
        /// 存储顶点信息
        /// </summary>
        public string data;
        /// <summary>
        /// 边表头
        /// </summary>
        public EdgeNode firstedge;

        public VertexNode(string data)
        {
            this.data = data;
            this.firstedge = null;
        }
    }
    /// <summary>
    /// 有向图
    /// </summary>
    class Digraph
    {
        /// <summary>
        /// 顶点数组
        /// </summary>
        public VertexNode[] verList;
        /// <summary>
        /// 图顶点数
        /// </summary>
        public int numVertexes;
        /// <summary>
        /// 图边数
        /// </summary>
        public int numEdges;

        /// <summary>
        /// 创建图信息
        /// </summary>
        /// <param name="m">顶点数</param>
        /// <param name="n">边数</param>
        /// <param name="data">顶点信息集合</param>
        public Digraph(int m, int n, string data)
        {
            numVertexes = m;
            numEdges = n;
            string[] fruit = data.Split(',');
            verList = new VertexNode[numVertexes];
            for (int i = 0; i < this.numVertexes; i++)
            {
                verList[i] = new VertexNode(fruit[i]);
            }
        }
    }


    public class OperGL
    {

        private Digraph GL = new Digraph(6, 8, "A,B,C,D,E,F");

        /// <summary>
        /// 创建边
        /// </summary>
        /// <param name="fromV">起点</param>
        /// <param name="toV">终点</param>
        /// <param name="weight">权重</param>
        public void InitEdges(int fromV, int toV, int weight = 0)
        {
            EdgeNode temp = new EdgeNode(toV, weight);//边


            if (GL.verList[fromV].firstedge == null)//如果表头为空，则把生成的边表节点放进去
            {
                GL.verList[fromV].firstedge = temp;
            }
            else//如果表头不为空，则往下找next，找到空的为止
            {
                EdgeNode ee = GL.verList[fromV].firstedge;
                while (true)
                {
                    if (ee.next == null)
                    {
                        ee.next = temp;
                        break;
                    }
                    else
                    {
                        ee = ee.next;
                    }
                }
            }

            ++GL.verList[toV].inDeg;//添加一条弧，增加入度
        }


        /// <summary>
        /// 创建有向图
        /// </summary>
        public void CreatAlGraph()
        {

            InitEdges(0, 1, 5);
            InitEdges(0, 2, 6);
            InitEdges(0, 3, 4);
            InitEdges(1, 2, 2);
            InitEdges(2, 3, 3);
            InitEdges(3, 4, 1);
            InitEdges(4, 5, 3);
            InitEdges(3, 5, 5);

        }

        /// <summary>
        /// 展示图信息
        /// </summary>
        public void ShowALGraph()
        {
            for (int i = 0; i < GL.numVertexes; i++)
            {
                Console.WriteLine("顶点" + i + "为：" + GL.verList[i].firstedge + "--FirstEdge--");
                EdgeNode temp = new EdgeNode(0, 0);
                temp = GL.verList[i].firstedge;
                while (temp != null)
                {
                    Console.WriteLine(temp.adjvex + "--Next--");
                    temp = temp.next;
                }
                Console.WriteLine("END" + GL.verList[i].data);
            }
        }

        /// <summary>
        /// 事件最早发生时间
        /// </summary>
        int[] etv;
        /// <summary>
        /// 时间最迟发生时间
        /// </summary>
        int[] ltv;
        /// <summary>
        /// 用于存储拓扑序列的栈
        /// </summary>
        Stack<int> stack2 = new Stack<int>();

        /// <summary>
        /// 拓扑排序，用于关键路径计算
        /// </summary>
        /// <returns></returns>
        public bool TopologicalSort()
        {

            EdgeNode e;
            int i, k, gettop;

            int count = 0;//统计输出顶点的个数
            Stack<int> stack = new Stack<int>();//存储入度为0 的顶点


            for (i = 0; i < GL.numVertexes; i++)
            {
                if (GL.verList[i].inDeg == 0)
                {
                    stack.Push(i);//将入度为0的顶点入栈
                }
            }

            etv = new int[GL.numVertexes];
            for (i = 0; i < GL.numVertexes; i++)
            {
                etv[i] = 0;
            }
            while (stack.Count != 0)
            {
                gettop = stack.Pop();//出栈
                //Console.Write(GL.verList[gettop].data);//打印此顶点
                count++;//统计输出顶点数
                stack2.Push(gettop);
                for (e = GL.verList[gettop].firstedge; e != null; e = e.next)//对顶点弧表遍历
                {
                    k = e.adjvex;
                    if ((--GL.verList[k].inDeg) == 0)//将k号顶点领接点的入度减1
                    {
                        stack.Push(k);//为0则入栈
                    }
                    if (etv[gettop] + e.weight > etv[k])
                    {
                        etv[k] = etv[gettop] + e.weight;
                    }
                }

            }
            if (count < GL.numVertexes)//如果count小于顶点数，说明存在环
            {
                return false;
            }
            else
            {
                return true;
            }
        }

        /// <summary>
        /// 求关键路径，GL为有向网，输出GL的各项关键活动
        /// </summary>
        public void CriticalPath()
        {
            EdgeNode e;
            int gettop, k;

            int ete, lte;//声明活动最早发生时间和最迟发生时间变量
            TopologicalSort();
            ltv = new int[GL.numVertexes];
            for (int i = 0; i < GL.numVertexes; i++)
            {
                ltv[i] = etv[GL.numVertexes - 1];//初始化ltv
            }
            while (stack2.Count != 0)//计算ltv
            {
                gettop = stack2.Pop();//将拓扑序列出栈，后进先出
                for (e = GL.verList[gettop].firstedge; e != null; e = e.next)
                {
                    //求各顶点事件的最迟发生时间ltv值
                    k = e.adjvex;
                    if (ltv[k] - e.weight < ltv[gettop])//求各顶点事件最晚发生时间ltv
                    {
                        ltv[gettop] = ltv[k] - e.weight;
                    }
                }
            }
            for (int j = 0; j < GL.numVertexes; j++)//求ete，lte和关键活动
            {
                for (e = GL.verList[j].firstedge; e != null; e = e.next)
                {
                    k = e.adjvex;
                    ete = etv[j];//活动最早发生时间
                    lte = ltv[k] - e.weight;//活动最迟发生时间
                    if (ete == lte)//两者相等即在关键路径上
                    {
                        Console.Write("<{0},{1}>length:{2},", GL.verList[j].data, GL.verList[k].data, e.weight);
                    }
                }
            }
        }
    }

}