回溯(Flash back)学习
Posted 楠c
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了回溯(Flash back)学习相关的知识,希望对你有一定的参考价值。
回溯是一种通过穷举所有可能情况来找到所有解的思想。如果一个候选解最后被发现并不是可行解,回溯思想会舍弃它,并在前面的一些步骤做出一些修改,并重新尝试找到可行解。回溯一般会结合在搜索算法中
电话号码组合

Map建立号码与字符串映射。
在代码中,DFS里,curStr+e即一个回溯的过程。例如当前是cur是空串,e依次被映射为abc,先从a开始,继续调用DFS,由于index++,所以e依次被映射到def,所以curStr现在是a,就开始和def两两组合,符合条件入结果数组。执行完后回溯,curStr成为b,又开始新的一轮。
class Solution {
private:
unordered_map<char,string> Map;
void DFS(const string& digits,vector<string>& Allret,string curStr,int idx)
{
if(idx==digits.size())
{//只有和字符串大小相等时才加入数组当中,然后结束当前深搜
Allret.push_back(curStr);
return;
}
//取出当前字符对应的字符串
string curMap=Map[digits[idx]];
for(char e:curMap)
{
//curStr+e,即为一个回溯的过程
//从DFS返回他就又成为了curStr
//curStr+e是个临时变量,所以形参不能是引用
DFS(digits,Allret,curStr+e,idx+1);
}
}
public:
vector<string> letterCombinations(string digits) {
vector<string> Allret;
if(digits.size()==0)
return Allret;
Map={{'2',"abc"},{'3',"def"},{'4',"ghi"},{'5',"jkl"},{'6',"mno"},{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"}};
DFS(digits,Allret,"",0);
return Allret;
}
};
组合总和
最精华的部分就是DFS中的for循环,从prev开始,因为题目中的2 2 3和3 2 2这种组合不能重复出现,即现在是3,不能向前回退去找2。又因为当前元素可以重复,所以在此调用的时候,需要从i开始,即形参prev的实参为i。
class Solution {
private:
void DFS(vector<int>& candidates, int target,vector<vector<int>>& ret,vector<int>& temp,int sum,int prev)
{
//大于返回,等于,先添加进结果数组再返回。
if(sum>=target)
{
if(sum==target)
{
ret.push_back(temp);
}
return;
}
//从上一个开始,例如2 2 3,回溯之后为2 2,可以从2 2开始继续试探
//不能从第一个重新开始,因为有可能造成 2 2 3 和 3 2 2这种情况,就成为了重复的组合
for(int i=prev;i<candidates.size();i++)
{
temp.push_back(candidates[i]);
//回溯
//1. 当前Dfs结束sum+candidates[i],就会变成sum
//2. temp里面也要删
//prev继续传i表示,上一个相加的位可以重复使用
DFS(candidates,target,ret,temp,sum+candidates[i],i);
temp.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ret;
if(candidates.empty())
return ret;
vector<int> temp;
DFS(candidates,target,ret,temp,0,0);
return ret;
}
};
二进制手表
分钟和小时的组合不一样,所以要区分开,依旧是i=prev,prev代表上次的位置,因为它不允许向前回退,但又由于上次的元素不能重复,所以下次调用时,形参的prev实参需要变成i+1。
回溯的过程,结合代码注释,在体会体会。
class Solution {
private:
vector<int> v;
// v={1,2,4,8,16,32};
void DFS(vector<string>& ret,int hour,int minutes,int prev,int turnedOn)
{
//边界
if(hour>=12||minutes>=60)
{
return;
}
//每次减一,等于0,说明组合满足,时放入结果数组
//例如turned=2,就是两两组合
if(turnedOn==0)
{
//m和h:先用整形计算,后转换成字符串
string m=to_string(minutes);
//字符串小于两位,前面补个0
m=m.size()>=2?m:'0'+m;
string h=to_string(hour);
ret.push_back(h+":"+m);
return;
}
for(int i=prev;i<10;i++)
{
//小于6,先和分钟组合
if(i<6)
{ //从i=0开始,turnedOn为2-1。
//第一次搜索以1为基准,i<6算分钟,去匹配 1+2 1+4 1+8 1+16 1+32(即0:03,0:05,....)
// i>6算小时,去匹配 1:01 2:01 4:01 8:01
//回溯回来以2为基准, i<6算分钟,去匹配 2+4 2+8 2+16 2+32(即0:06,0:10,...)
// i>6算小时,去匹配 1:02 2:02 4:02 8:02
//处理完2回溯回来到3
//i+1表示下一次不算本身,例如以1为基准组合,从2开始。以2为基准组合,从4开始
DFS(ret,hour,minutes+v[i],i+1,turnedOn-1);
}//大于6,和小时组合
else
{
DFS(ret,hour+v[i-6],minutes,i+1,turnedOn-1);
}
}
}
public:
vector<string> readBinaryWatch(int turnedOn) {
vector<string> ret;
if(turnedOn>=9)
return ret;
//小时和分钟的前四个一样,那么写成一个,等会做个区分就可以
//用两个vector也可
v={1,2,4,8,16,32};
DFS(ret,0,0,0,turnedOn);
return ret;
}
};
字符串排列

题目的样例要求向前回退,即b可以匹配a,所以在循环中我们每次都要从0开始,但是这样肯定会有aaa,aab,aac,等这种一个元素重复使用的情况。
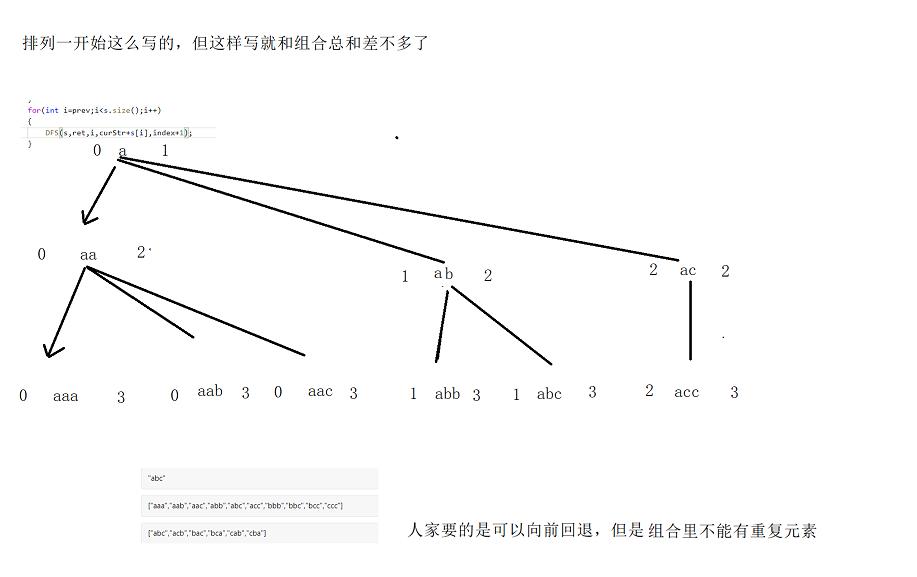

vis是一个标记数组

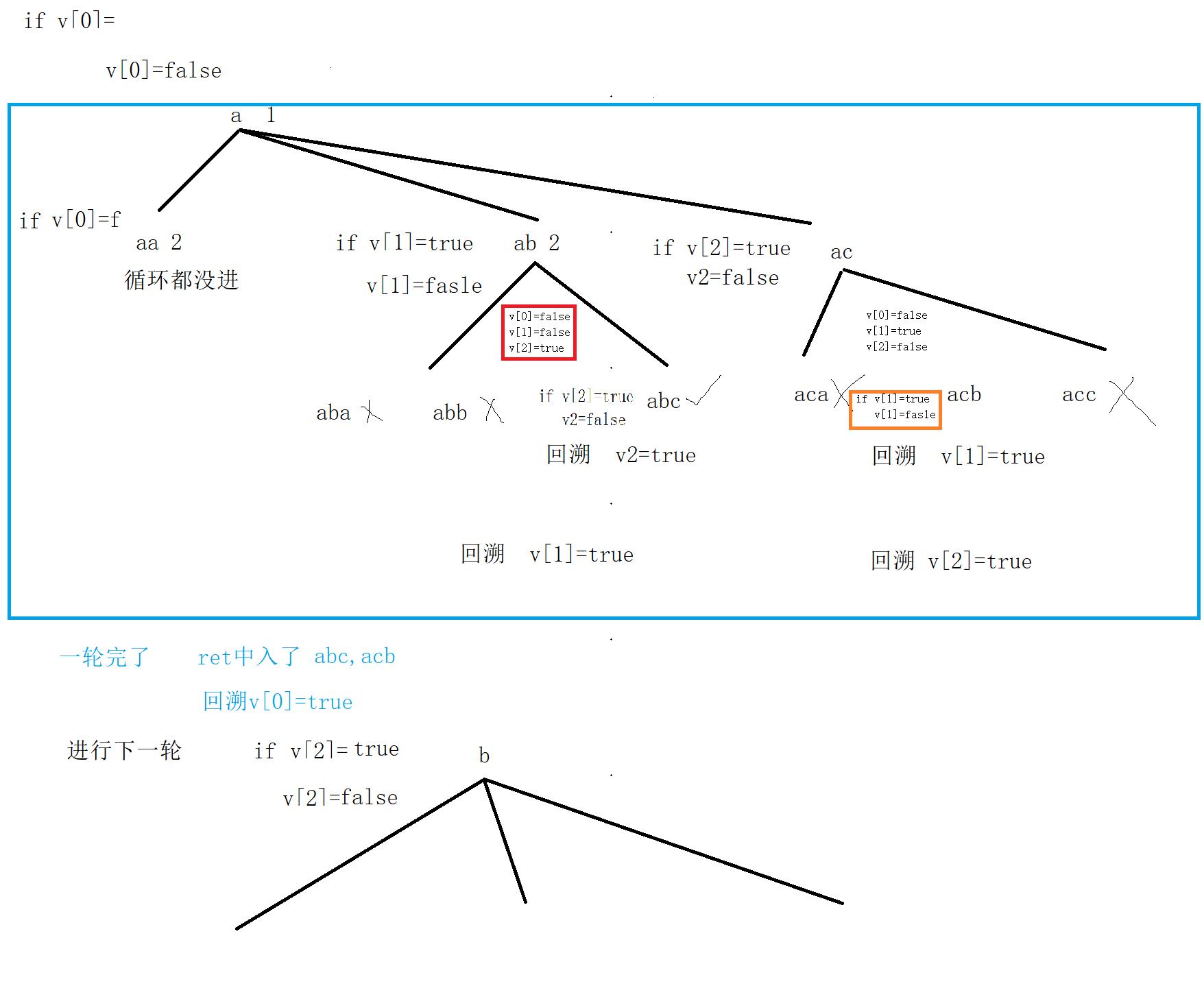
这样就避免了重复使用一个元素。

class Solution {
private:
void DFS(string s,unordered_set<string>& ret,vector<bool>& vis,string curStr,int index)
{
//放入哈希set当中,这样做的原因是防止字符串中有重复的例如"aab"
if(index==s.size())
{
ret.insert(curStr);
return;
}
for(int i=0;i<s.size();i++)
{
if(vis[i])
{
vis[i]=false;
DFS(s,ret,vis,curStr+s[i],index+1);
vis[i]=true;
}
}
}
public:
vector<string> permutation(string s) {
unordered_set<string> ret;
vector<bool> vis(s.size(),true);
DFS(s,ret,vis,"",0);
//去重之后再放进数组中返回
vector<string> ret1(ret.begin(),ret.end());
return ret1;
}
};
在和这两个对比一下


活字印刷
可以向前回退,但重复元素不能使用。即循环从0开始,且需要标记数组
class Solution {
private:
void DFS(string tiles,unordered_set<string>& ret,vector<bool>& vis,string curStr)
{
if(curStr!="")
{
ret.insert(curStr);
}
for(int i=0;i<tiles.size();i++)
{
if(vis[i])
{
vis[i]=false;
DFS(tiles,ret,vis,curStr+tiles[i]);
vis[i]=true;
}
}
}
public:
int numTilePossibilities(string tiles) {
unordered_set<string> ret;
vector<bool> vis(tiles.size(),true);
DFS(tiles,ret,vis,"");
return ret.size();
}
};
N皇后
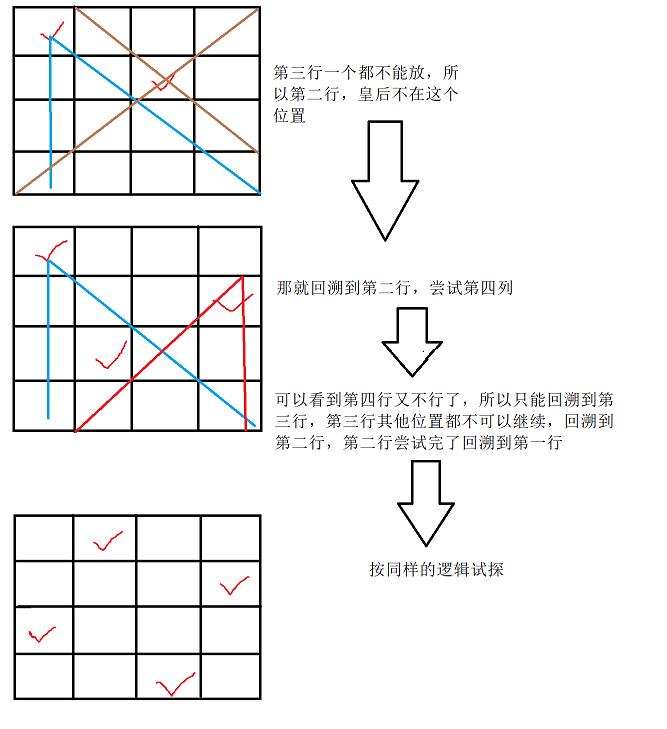
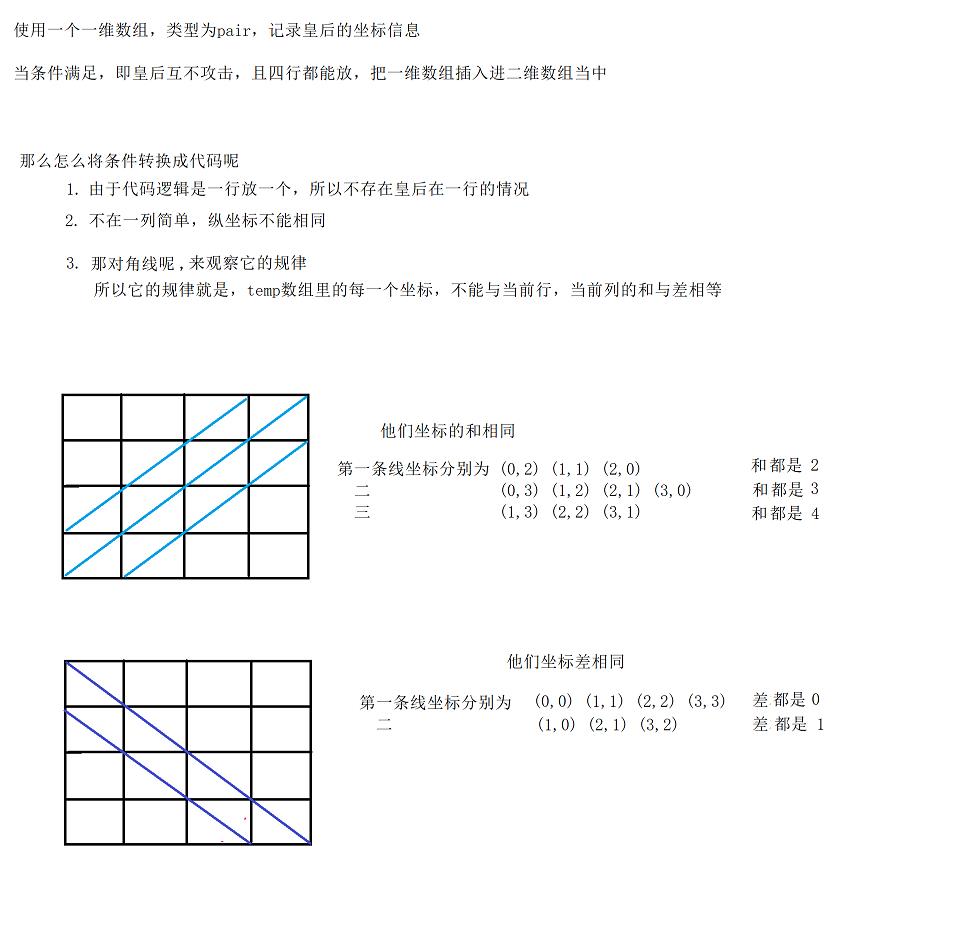
class Solution {
void DFS(vector<vector<pair<int,int>>>& ret,vector<pair<int,int>>& temp,int curRow,int n)
{
if(curRow==n)
{
//临时数组坐标全部符合,curRow才能加到n,才能入结果数组
ret.push_back(temp);
}
for(int col=0;col<n;col++)
{
//坐标有效才插入临时数组
//临时数组:(保护当前一种方法的所有皇后坐标)
if(isValid(temp,curRow,col))
{
temp.push_back(make_pair(curRow,col));
DFS(ret,temp,curRow+1,n);
temp.pop_back();
}
}
}
//皇后坐标是否有效
bool isValid(vector<pair<int,int>>& temp,int curRow,int col)
{
for(auto& e:temp)
{
if(e.second==col||e.first+e.second==curRow+col||e.first-e.second==curRow-col)
return false;
}
return true;
}
//输出有点奇怪,所以要转换
vector<vector<string>> transRet(vector<vector<pair<int,int>>> ret,int n)
{
vector<vector<string>> vv;
for(auto& v:ret)
{
//观察输出,二维数组,每个一维数组由4个string组成,每个string都有四个'.'
vector<string> vs(n,string(n,'.'));
for(auto& e:v)
{
vs[e.first][e.second]='Q';
}
vv.push_back(vs);
}
return vv;
}
public:
vector<vector<string>> solveNQueens(int n) {
vector<vector<pair<int,int>>> ret;
vector<pair<int,int>> temp;
DFS(ret,temp,0,n);
vector<vector<string>> vv=transRet(ret,n);
return vv;
}
};
N皇后||
我们用一维临时数组来存储当前方法的皇后坐标。有几种方法就插入几次二维数组。最后二维数组的size就是方法数量
class Solution {
private:
void DFS(vector<vector<pair<int,int>>>& ret,vector<pair<int,int>>& temp,int curRow,int n)
{
if(curRow==n)
{
ret.push_back(temp);
return;
}
for(int col=0;col<n;col++)
{
if(isVaild(temp,curRow,col))
{
temp.push_back(make_pair(curRow,col));
DFS(ret,temp,curRow+1,n);
temp.pop_back();
}
}
}
bool isVaild(vector<pair<int,int>> temp,int curRow,int col)
{
for(auto&e :temp)
{
if(col==e.second||curRow+col==e.first+e.second||curRow-col==e.first-e.second)
return false;
}
return true;
}
public:
int totalNQueens(int n) {
vector<vector<pair<int,int>>> ret;
vector<pair<int,int>> temp;
DFS(ret,temp,0,n);
return ret.size();
}
};
以上是关于回溯(Flash back)学习的主要内容,如果未能解决你的问题,请参考以下文章