8.16 记忆增强神经网络:MANN神经网络图灵机
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了8.16 记忆增强神经网络:MANN神经网络图灵机相关的知识,希望对你有一定的参考价值。
文章目录
👉8.7 Meta learning元学习全面理解、MAML、Reptile
记忆增强神经网络(MANN)进行元学习解决one-shot问题。
传统的基于梯度的网络需要学习大量的数据,通常是通过大量的迭代训练。当遇到新数据时,模型必须低效地重新学习它们的参数,以便在不产生灾难性干扰的情况下充分整合新信息。
神经图灵机是MANN的一个完全可微的实现。它由一个记忆库和控制器组成,控制器如前馈网络或LSTM,使用多个读写头与外部记忆模块交互。NTM外部记忆模块中的记忆编码和信息检索是快速的,每个时间步都有可能将向量表示放入或取出记忆。
这种能力使NTM成为元学习和低概率预测的完美候选,因为它既可以通过其权重的缓慢更新进行长期记忆,也可以通过其外部记忆模块进行短期记忆。因此,如果一个NTM可以学习通用的策略,什么样的表征应该放入记忆中和如何使用这些表征预测。这样,它就可以利用自己的速度对只见过一次的数据做出准确的预测。
mann快速吸收新数据的能力,并利用这些数据在少量样本后做出准确的预测。
mann能够在具有显著短期和长期记忆需求的任务中进行元学习。仅在几次训练后,就成功地对从未见过的Omniglot类进行了人类精确度的分类,并基于少量样本进行了原则性的函数估计。此外,还引入了一种最近最少使用方法来写外部记忆,而不是像NTM的原始实现那样使用额外记忆位置寻址。
mann结合了两个方面的优点:一是通过梯度下降慢慢学习抽象方法以获得原始数据的有用表征,二是通过外部记忆模块在一次训练后快速获取从未见过的信息。这种组合支持稳健的元学习,扩展了深度学习可以有效应用的问题范围。
1.神经网络图灵机
前言
一般的神经网络不具有记忆功能,输出的结果只基于当前的输入;而LSTM网络的出现则让网络有了记忆:能够根据之前的输入给出当前的输出。但是,LSTM的记忆程度并不是那么理想,对于比较长的输入序列,LSTM的最终输出只与最后的几步输入有关,也就是long dependency问题,当然这个问题可以由注意力机制解决,然而却不能从根本上解决长期记忆的问题,原因是由于LSTM是假设在时间序列上的输入输出:由t-1时刻得到t时刻的输出,然后再循环输入t时刻的结果得到t+1时刻的输出,这样势必会使处于前面序列的输入被淹没,导致这部分记忆被“丢掉“。
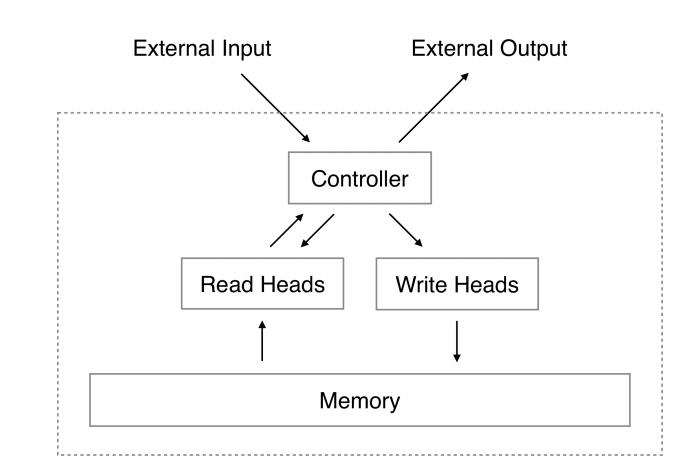
神经图灵机通过引入外部记忆解决了这个问题。 举个简单的例子,我们人类在记忆一些事情的时候,除了用脑袋记,还会写在备忘录上,当我们想不起来的时候,就可以去翻阅备忘录,从而获得相关的记忆。神经图灵机模仿人类记忆的过程:其中的控制器(controller)相当于我们人类的大脑,用于把输入事物的特征提取出来;外部记忆(memory)相当于我们的备忘录,把事物的特征记录在上面,那么完整的过程就是:控制器将当前输入转化为特征,写入记忆,再读取与当前输入特征有关的记忆作为最后的输出。整个过程与图灵机的读写很像,只不过神经图灵机这里让所有的读写操作都可微分化,因此可以用神经网络误差后向传播的方式去训练模型。
神经图灵机除了在memory中进行读之外,还可以在memory中写。
图
一
:
神
经
图
灵
机
图一:神经图灵机
图一:神经图灵机
从图一可以看出,神经图灵机包含两个基本组成部分:神经网络控制器和记忆库。
- 控制器: 这是一个基础的前馈神经网络或者RNN,其主要负责从记忆库中读取信息或者在记忆库中写入信息,控制器通过输入输出向量和外界交互。
- 记忆库: 记忆库通常是记忆矩阵,可以进行存储信息。记忆矩阵一般是二维 N × M N \\times M N×M ,通过使用控制器在记忆矩阵进行读或写信息,因此,控制器可以从额外的环境中接受内容,并且能够通过与记忆矩阵的交互来做出反应。
- 读头和写头:由控制器生成,读头和写头是包含记忆库位置的两个指针,记忆库位置指的是需要读取的位置和需要写入的位置。
读记忆 (Read Heads)
令
M
t
M_t
Mt 为
N
×
M
N\\times M
N×M 在时间
t
t
t 的记忆矩阵,其中
N
N
N 是记忆位置的数目,而
M
M
M是每个位置的向量的大小。设
w
t
\\mathrm{w}_{t}
wt是一个在
t
t
t时刻读头输出的在
N
N
N个位置上的权重向量。由于所有的权重都是归一化的,
w
t
\\mathbf{w}_{t}
wt中的
N
N
N 个元素
w
t
(
i
)
w_{t}(i)
wt(i)服从以下约束:
∑
i
w
t
(
i
)
=
1
,
0
≤
w
t
(
i
)
≤
1
,
∀
i
(1)
\\large \\color{green}{\\sum_{i} w_{t}(i)=1, \\quad 0 \\leq w_{t}(i) \\leq 1, \\forall i\\tag{1}}
i∑wt(i)=1,0≤wt(i)≤1,∀i(1)
那么,时刻
t
t
t读取到的值
r
t
\\mathrm{r}_{t}
rt ,由记忆矩阵中行向量
M
t
(
i
)
\\mathbf{M}_{t}(i)
Mt(i) 与权重相乘组成:
r
t
=
∑
i
w
t
(
i
)
M
t
(
i
)
(2)
\\large \\color{green}{\\mathbf{r}_{t} =\\sum_{i} w_{t}(i) \\mathbf{M}_{t}(i)\\tag{2}}
rt=i∑wt(i)Mt(i)(2)
这显然是对记忆和权重都是可微的。其中
r
t
\\mathrm{r}_{t}
rt长度为
M
M
M
写记忆(Write Heads)
从LSTM中的输入门和遗忘门中获得灵感, 将每个写入分解为两个部分:删除和添加。
给定写头在
t
t
t时刻输出的一个权重
w
t
\\mathbf{w}_{t}
wt,以及一个删除向量
e
t
\\mathbf{e}_{t}
et,其
M
M
M元素都在
(
0
,
1
)
(0,1)
(0,1)范围内,前一个时间步长的记忆向量
M
t
−
1
(
i
)
\\mathbf{M}_{t-1}(i)
Mt−1(i)做出如下修改:
M
~
t
(
i
)
=
M
t
−
1
(
i
)
[
1
−
w
t
(
i
)
e
t
]
(3)
\\large \\color{green}{\\tilde{\\mathbf{M}}_{t}(i)=\\mathbf{M}_{t-1}(i)\\left[1-w_{t}(i) \\mathbf{e}_{t}\\right]\\tag{3}}
M~t(i)=Mt−1(i)[1−wt(i)et](3)
其中
1
\\mathbf{1}
1是元素都是1的行向量,对记忆位置的乘法是逐点操作。因此,只有当位置的权重和删除元素都为1时,记忆位置的元素才被重置为0;如果两个中有一个为 0,记忆就保持不变。当多个写头给出了,删除操作可以按照任意的顺序进行,因为乘法实际上是可交换的。
每个写头同样还会产生一个长度为
M
M
M 的添加向量
a
t
\\mathbf{a}_{t}
at,这个会在每个删除步后执行添加记忆:
M
t
(
i
)
=
M
~
t
(
i
)
+
w
t
(
i
)
a
t
(4)
\\large \\color{green}{\\mathbf{M}_{t}(i) = \\tilde{\\mathbf{M}}_{t}(i)+w_{t}(i) \\mathbf{a}_{t}\\tag{4}}
Mt(i)=M~t(i)+wt(i)at(4)
另外,多个头进行的加法操作的顺序是不相关的。所有写头上的删除和添加操作产生了在时间
t
t
t 最终的记忆内容。删除和添加操作都是可微的,删除和添加向量有
M
M
M 个独立的部分,这样可以更好地控制在每个记忆位置上的那些需要修改的元素。所以写记忆为
M
t
(
i
)
=
M
t
−
1
(
i
)
−
w
t
(
i
)
e
t
⋅
M
t
−
1
(
i
)
+
w
t
(
i
)
a
t
(5)
\\large \\color{green}{\\mathbf{M}_{t}(i) =\\mathbf{M}_{t-1}(i) -w_{t}(i) \\mathbf{e}_{t} \\cdot \\mathbf{M}_{t-1}(i)+w_{t}(i) \\mathbf{a}_{t} \\tag{5}}
Mt(i)=Mt−1(i)−wt(i)et⋅Mt−1(i)+wt(i)at(5)
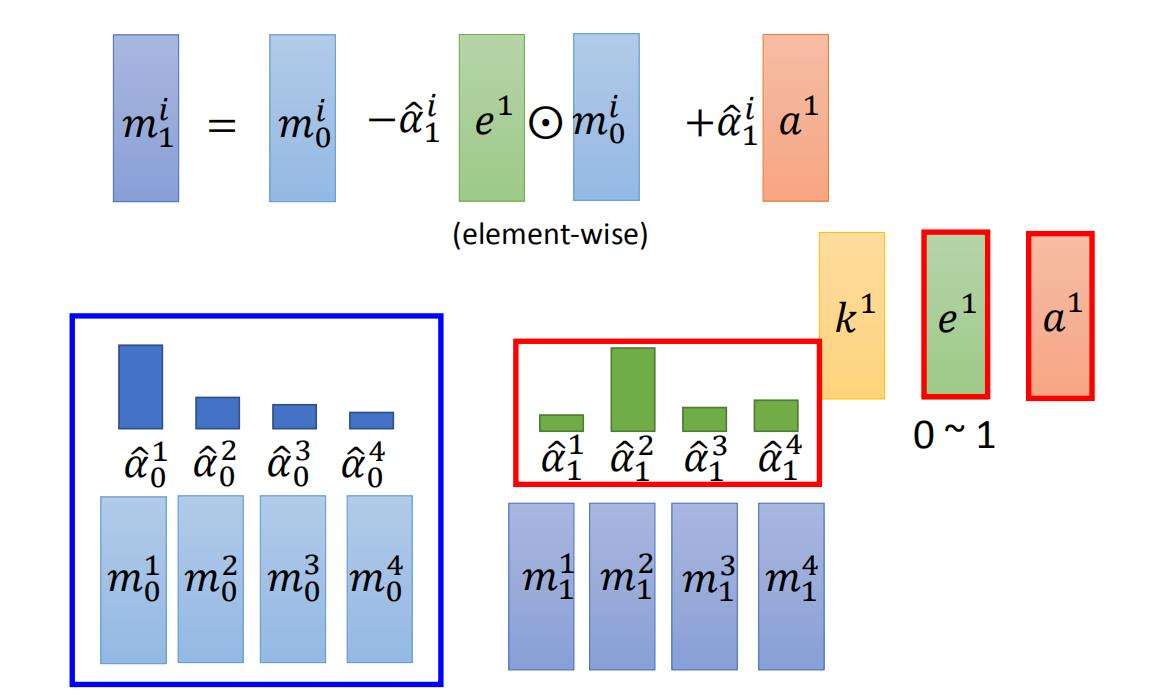
继续看原理图, 在图中我们算出了 e 1 e^{1} e1 和 a 1 , e 1 a^{1}, e^{1} a以上是关于8.16 记忆增强神经网络:MANN神经网络图灵机的主要内容,如果未能解决你的问题,请参考以下文章