7.5图卷积编码器-解码器
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了7.5图卷积编码器-解码器相关的知识,希望对你有一定的参考价值。
1、前言
图卷积编码是让编码器能够访问丰富的语法信息,但让它决定语法的哪些方面对MT(机器翻译)有益,而不是对语法和翻译任务之间的交互执行严格的约束,因为严格的语法限制通常会损害机器翻译。
基于 Seq2seq +Attention的NMT系统,将源句词表示为编码器中的潜在特征向量,并在生成翻译时使用这些向量。
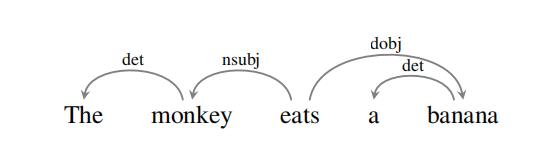
图卷积编码目标是将源词的语法邻域信息自动合并到这些特征向量中,从而潜在地提高翻译输出的质量。因为向量对应于单词,所以很自然地使用依赖语法。依赖树(见图1)表示单词之间的句法关系:例如,monkey是谓语eat的主语,banana是谓语eat的宾语。
图
1
:
依
赖
树
图1:依赖树
图1:依赖树
使用GCN生成单词的语法感知特征表征,GCN可以被视为基于节点的k阶邻域(即距离节点最多k跳的节点)计算节点(即实值向量)的潜在特征表征。
2、图卷积神经网络
GCN是一个多层神经网络,它直接在图上运行,将节点的邻域信息编码为实值向量。在每个GCN层中,信息沿着图的边流动;换句话说,每个节点接收来自其所有邻居的消息。当多个GCN层被堆叠时,关于更大邻居的信息就会被集成。例如,在第二层中,一个节点将从它的邻居接收信息,但是这些信息已经包含了来自它们各自的邻居的信息。通过选择GCN层数, 调节了信息传播的距离:在 k k k层中,一个节点接收来自邻居的信息最多有 k k k个跳数。
形式上,考虑一个无向图 G = \\mathcal{G}= G= ( V , E ) (\\mathcal{V}, \\mathcal{E}) (V,E),其中 V \\mathcal{V} V是一个 n n n节点的集合,而 E \\mathcal{E} E是一个边的集合。每个节点都被假定是连接到自己的,即 ∀ v ∈ V : ( v , v ) ∈ E \\forall v \\in \\mathcal{V}:(v, v) \\in \\mathcal{E} ∀v∈V:(v,v)∈E。
设
X
∈
R
d
×
n
X \\in \\mathbb{R}^{d \\times n}
X∈Rd×n是一个包含所有
n
n
n节点及其特征的矩阵,其中
d
d
d是特征向量的维数。
X
X
X将包含单词嵌入,但通常它可以包含任何类型的特征。对于1层GCN,新的节点表征计算如下:
h
v
=
ρ
(
∑
u
∈
N
(
v
)
W
x
u
+
b
)
\\mathbf{h}_{v}=\\rho\\left(\\sum_{u \\in \\mathcal{N}(v)} W \\mathbf{x}_{u}+\\mathbf{b}\\right)
hv=ρ⎝⎛u∈N(v)∑Wxu+b⎠⎞
其中
W
∈
R
d
×
d
W \\in \\mathbb{R}^{d \\times d}
W∈Rd×d是一个权重矩阵,
b
∈
R
d
\\mathbf{b} \\in \\mathbb{R}^{d}
b∈Rd是一个偏置向量。
ρ
\\rho
ρ是一个激活函数,例如ReLU。
N
(
v
)
\\mathcal{N}(v)
N(v)是
v
v
v的邻居集合,这里我们假设
v
v
v总是包含它自己。为了允许信息在多个跃点上流动,需要堆叠GCN层。递归计算如下:
h
v
(
j
+
1
)
=
ρ
(
∑
u
∈
N
(
v
)
W
(
j
)
h
u
(
j
)
+
b
(
j
)
)
\\mathbf{h}_{v}^{(j+1)}=\\rho\\left(\\sum_{u \\in \\mathcal{N}(v)} W^{(j)} \\mathbf{h}_{u}^{(j)}+\\mathbf{b}^{(j)}\\right)
hv(j+1)=ρ⎝⎛u∈N(v)∑W(j)hu(j)+b(j)⎠⎞
其中j索引层,和
h
v
(
0
)
=
x
v
\\mathbf{h}_{v}^{(0)}=\\mathbf{x}_{v}
hv(0)=xv
3、语法GCN
方向性
为了处理边的方向性,分别对入边和出边使用权重矩阵。遵循这样的约定:在依赖树中,头指向它们的依赖项,因此,输出边用于 head-to-dependent 的连接,传入边用于dependent-to-head的连接。修改方向性的循环计算,得到:
h
v
(
j
+
1
)
=
ρ
(
∑
u
∈
N
(
v
)
W
dir
(
u
,
v
)
(
j
)
h
u
(
j
)
+
b
dir
(
u
,
v
)
(
j
)
)
\\mathbf{h}_{v}^{(j+1)}=\\rho\\left(\\sum_{u \\in \\mathcal{N}(v)} W_{\\operatorname{dir}(u, v)}^{(j)} \\mathbf{h}_{u}^{(j)}+\\mathbf{b}_{\\operatorname{dir}(u, v)}^{(j)}\\right)
hv(j+1)=ρ⎝⎛u∈N(v)∑Wdir(u,v)(j)hu(j)+bdir(u,v)(j)⎠⎞
其中
dir
(
u
,
v
)
\\operatorname{dir}(u, v)
dir(u,v)选择与
u
u
u和
v
v
v之间的边的方向性相关的权值矩阵(即
W
I
N
W_{\\mathrm{IN}}
WIN :
u
u
u -to-
v
,
W
OUT
v, W_{\\text {OUT }}
v,WOUT :
v
v
v -to-
u
u
u ,
W
LOOP
W_{\\text {LOOP }}
WLOOP :
v
v
v -to-
v
v
v )。注意,自循环是单独建模的,因此现在有三倍于非定向GCN的参数。
标签
考虑到上述方向性的修改,使GCN对标签敏感是很简单的。不再为每个方向使用单独的矩阵,现在为每个方向和标签组合定义单独的矩阵:
h
v
(
j
+
1
)
=
ρ
(
∑
u
∈
N
(
v
)
W
lab
(
u
,
v
)
(
j
)
h
u
(
j
)
+
b
lab
(
u
,
v
)
(
j
)
)
\\mathbf{h}_{v}^{(j+1)}=\\rho\\left(\\sum_{u \\in \\mathcal{N}(v)} W_{\\operatorname{lab}(u, v)}^{(j)} \\mathbf{h}_{u}^{(j)}+\\mathbf{b}_{\\operatorname{lab}(u, v)}^{(j)}\\right)
hv(j+1)=ρ⎝⎛u∈N(v)∑Wlab(u,v)(j)hu(j)+blab(u,v)(j)⎠⎞
将一条边的方向性直接合并到它的标签中。
重要的是,为了防止过度参数化,只有偏置项是特定于标签的,换句话说: W lab ( u , v ) = W dir ( u , v ) W_{\\operatorname{lab}(u, v)}=W_{\\operatorname{dir}(u, v)} Wlab(u,v)=Wdir(u,v)
生成的语法GCN如图2所示(显示在CNN之上,将在后面的小节中解释)。
逐边门
句法GCN还包括门,可以降低单个边的贡献。它们还允许模型处理嘈杂的预测结构,即忽略潜在的错误的语法边缘。对于每条边,一个标量门的计算方法如下: 以上是关于7.5图卷积编码器-解码器的主要内容,如果未能解决你的问题,请参考以下文章
g
u
,
v
(
j
)
=
σ
(
h
u
(
j
)
⋅
w