opencv学习笔记第七篇：离散傅里叶变换

Posted 2021-06-30 非晚非晚

1. 离散傅里叶变换原理

离散傅里叶变换(Discrete Fourier Transform, DFT)， 是指傅里叶变换在时域和频域都呈现离散的形式，将时域信号的采样变换为在离散时间傅里叶变换(DTFT)频域的采样。

对一幅图使用傅里叶变换就是将它分解成正弦和余弦两部分，也就是图像从空间域(spatial domain)转换到频域(frequency domain)。

这一转换的理论基础为：

任意函数都可以表示成无数个正弦和余弦函数的和的形式。傅里叶变换就是一个用来将函数分解的工具。

二维图像的傅里叶变换可以用以下数学公式表示：

$$F(k,l)=\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}f(i,j)e^{-i2\pi \frac{ki}{N}\frac{lj}{N}}$$

$$e^{ix}=cosx+isinx$$

其中：f是空间域(spatial domain)值，F是频域(frequency domain)的值

在频域里面，对于一幅图像，高频部分代表了图像细节、纹理信息；低频部分代表了图像的轮廓信息。因此可以通过傅里叶变换可以做到图像增强与图像去噪、图像分割之边缘检测、图像特征提取、图像压缩等作用。

2. 离散傅里叶变换相关函数

2.1 dft()函数

dft函数的作用是对一维或二维浮点数数组进行正向或反向离散傅里叶变换，其函数原型如下：

void dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0);

参数解释：

• src：输入矩阵，可以为实数或者虚数；
• dst：运算结果，其尺寸和类型取决于第三个参数flags。
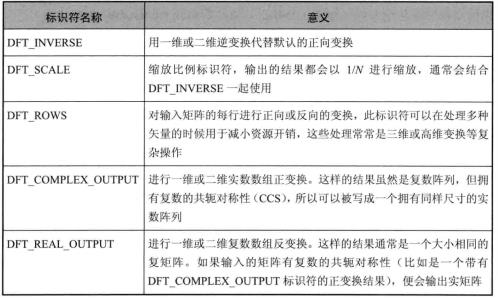
• flags：转化的标识符，其意义如下：
• nonzeroRows：设置为非零值时，表示只有输入矩阵的第一个非零行包含非零元素，或只有输出矩阵的第一个非零行包含非零元素。提高函数的处理效率。

2.2 getOptimalDTFSize()函数

getOptimalDTFSize函数返回给定向量尺寸的傅里叶最优尺寸大小。为了提高离散傅里叶变换的运行速度，需要扩充图像，而具体扩充多少，有这个函数决定。它的函数原型如下：

int getOptimalDFTSize(int vecsize);

参数解释：

• vecsize：向量尺寸，即图片的rows、clos。

2.3 copyMarkBorder()函数

copyMarkBorder函数的作用是扩充图像边界，其函数原型如下：

void copyMakeBorder(InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar& value=Scalar() )；

参数解释：

• src：输入图像，即源图像。
• dst：函数调用后的结果，和源图像尺寸和类型一致；
• top、bottom、left和right：源图像的四个方向上扩充多少个像素。
• borderType：边界类型，常见取值为BORDER_CONSTANT。
• value：默认值Scalar()可以理解为默认参数为0，当borderType的取值为BORDER_CONSTANT时，这个参数表示边界值。

2.4 magnitude()函数

magnitude用于计算二维矢量的幅值。其函数原型如下：

C++: void magnitude(InputArray x, InputArray y, OutputArray magnitude)；

参数解释：

• x：表示浮点型X坐标值，也就是实部；
• y：表示浮点型Y坐标值，也就是虚部；
• magnitude：输出的赋值，与第一个参数x有同样的尺寸和类型。

magnitude()函数原理如下：
$$dst(t)=\sqrt{x(I{)}^2+y(I{)}^2}$$

2.5 log()函数

log函数的功能是计算每个数组元素绝对值的自然对数。其函数原型如下：

void log(InputArray src, OutputArray dst);

参数解释：

• src：表示输入图像；
• dst：表示输出图像；

log函数原理如下：

$$dst(I)=\{\begin{array}{lc}\log |src(I)|& ifsrc(I)!=0\\ C& otherwise\end{array}$$

2.6 normalize()函数

normalize函数的功能为进行矩阵归一化。其函数原型如下：

void normalize(InputArray src, OutputArray dst, double alpha=1, double beta=0, int norm_type=NORM_L2, int dtype=-1, InputArray mask=noArray() )

参数解释：

• src：输入图像，即源图像
• dst输出图像，与源图像有同样的尺寸和类型
• alpha：归一化后的最小值，默认值1；
• beta：归一化后的最大值，默认值0；
• norm_type：归一化类型，norm_type类型有下列几种
• dtype：当该参数为负数时，输出数组的类型与输入数组的类型相同，否则输出数组与输入数组只是通道数相同，而depth = CV_MAT_DEPTH(dtype)
• mask：操作掩膜版，用于指示函数是否仅仅对指定的元素进行操作。

norm_type的类型：

• NORM_INF: 归一化数组的C-范数（绝对值的最大值）
• NORM_L1: 归一化数组的L1-范数（绝对值的和）
• NORM_L2: 归一化数组的L2-范数（欧几里得）
• NORM_MINMAX: 数组的数值被平移或缩放到一个指定的范围，线性归一化，一般较常用。

3. 傅里叶变换程序实例

#include "opencv2/core.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"

#include <iostream>

using namespace cv;
using namespace std;

int main(int argc, char **argv)
{
    Mat I = imread("/home/liqiang/Data/vision/classic/lena.jpg", IMREAD_GRAYSCALE); //将读入的图像转灰度图
    if (I.empty())
    {
        cout << "Error opening image" << endl;
        return -1;
    }

    Mat padded; //expand input image to optimal size
    int m = getOptimalDFTSize(I.rows);
    int n = getOptimalDFTSize(I.cols); // on the border add zero values
    //扩充图像边界，上方和左方不做处理
    copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));

    Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
    Mat complexI;
    merge(planes, 2, complexI); // Add to the expanded another plane with zeros

    //傅里叶变换，输出到complex
    dft(complexI, complexI); // this way the result may fit in the source matrix

    // compute the magnitude and switch to logarithmic scale
    // => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
    //计算幅值，planes[0]为实部,planes[1]为虚部
    split(complexI, planes);                    // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
    magnitude(planes[0], planes[1], planes[0]); // planes[0] = magnitude
    Mat magI = planes[0];

    //! [log]
    magI += Scalar::all(1); // switch to logarithmic scale
    log(magI, magI);
    //! [log]

    //! [crop_rearrange]
    // crop the spectrum, if it has an odd number of rows or columns
    magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2));

    // rearrange the quadrants of Fourier image  so that the origin is at the image center
    int cx = magI.cols / 2;
    int cy = magI.rows / 2;

    Mat q0(magI, Rect(0, 0, cx, cy));   // Top-Left - Create a ROI per quadrant
    Mat q1(magI, Rect(cx, 0, cx, cy));  // Top-Right
    Mat q2(magI, Rect(0, cy, cx, cy));  // Bottom-Left
    Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right

    Mat tmp; // swap quadrants (Top-Left with Bottom-Right)
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);

    q1.copyTo(tmp); // swap quadrant (Top-Right with Bottom-Left)
    q2.copyTo(q1);
    tmp.copyTo(q2);
    //! [crop_rearrange]

    //! [normalize]
    normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a
                                              // viewable image form (float between values 0 and 1).
                                              //! [normalize]

    imshow("Input Image", I); // Show the result
    imshow("spectrum magnitude", magI);
    while(waitKey(0) !='q'){}

    return 0;
}

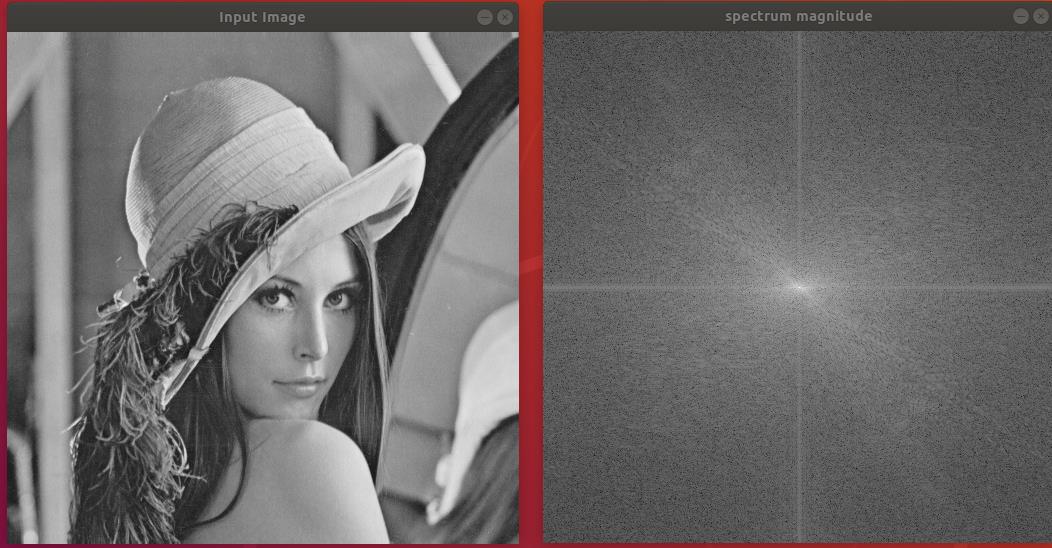
输出效果图：