数据结构知识点总复习
Posted karshey
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构知识点总复习相关的知识,希望对你有一定的参考价值。
考试范围
重点:第2、5、6、7、8章。
略考:第1,3章。
第四章不考。
不考的其他内容:
广义表、KMP、线索化二叉树、十字链表、邻接多重表、拓扑排序、关键路径、平衡二叉树,B树,B+树,分块查找,希尔排序,折半插入,基数排序,外部排序。
复习指南:课件,PTA。PTA所有主观题和课本后的所有习题。
本篇是课件的总结。可能不全。
第一章
本章重点:数据结构相关名词术语的含义。难点:时间复杂度的估算。
数据:是客观事物的符号表示。能被输入到计算机中被程序处理的符号的总称。
数据元素:也称顶点,结点或记录。数据的基本单位。
数据项:最小单位。
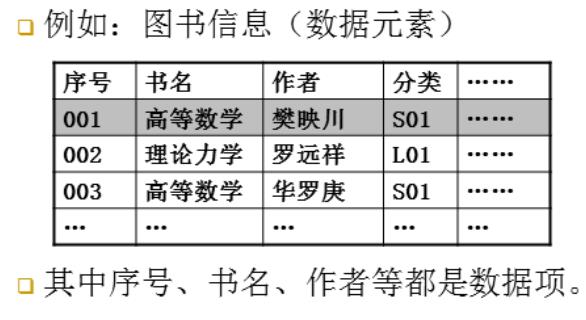
数据对象:性质相同的数据元素集合。
数据结构:带结构的相同性质数据元素集合。结构是一种或多种关系。
以上不知道怎么背,随便过过吧。
逻辑结构=数据元素+关系。
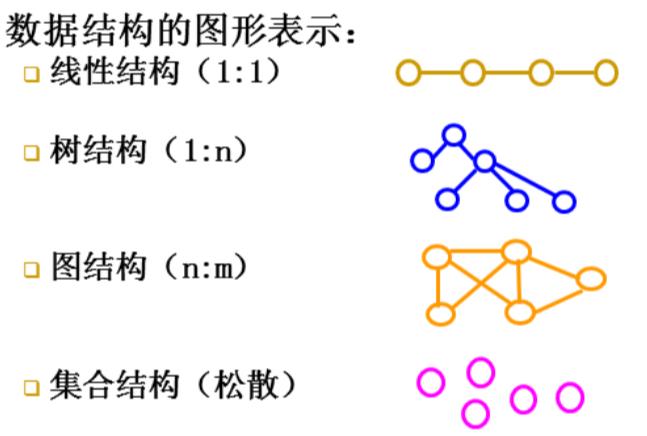
四类基本结构:
- 线性结构:一对一,如线性表,栈和队列,字符串,数组,广义表
- 树结构:一对多
- 图/网状结构:多对多
- 集合结构。
后三个是非线性结构。(即四类中除了线性结构的)
两种存储结构:顺序存储(数组),链式存储(结构体和指针)。
差别:
顺序存储:相邻位置表示元素逻辑关系。
链式存储:指针信息表示元素逻辑关系。
算法:
五特性:有穷,确定,可行,输入,输出。
优劣标准:正确性,可读性,健壮性,高效性。
时间复杂度:一般是最深层循环内的语句频度。
两个没什么用的表:(?)


第二章
重难点:顺序表和链表。
概念:非空的线性表或线性结构是一个有限数据元素的有序集合。
特点:存在唯一一个第一个,最后一个数据元素;每个数据元素只有一个前驱(除第一个)和后继(除最后一个)。
存储:连续地址。是随机存储结构。
线性表
线性表的一些操作:
GetElem:
i是位置。注意特判范围。第1个存在0号位,故取值要i-1;
if(i<1||i>=L.length) return ERROR;
e=L.elem[i-1];
LocateElem:存在就返回位序,不存在就返回0;
地址从0开始,位序从1开始。故return i+1;
for(int i=0;i<L.length;i++)
{
if(L.elem[i]==e) return i+1;
}
return 0;
线性表查找的算法时间效率:(n+1)/2;
InSert操作:
i的合法范围:1~L.length+1;
还要判断线性表是否满了:
if(L.length==MAXSIZE) return 0;
线性表插入移动的期望值:n/2;
Delete操作:
判断范围:i的合法范围:1~L.length;
if(i<1||i>L.length) return 0;
线性表删除移动的期望值:(n-1)/2;
| 线性表操作 | 移动期望值 |
|---|---|
| 查找 | (n+1)/2 |
| 插入 | n/2 |
| 删除 | (n-1)/2 |
链表
特点:结点位置任意,逻辑上相邻元素在物理上不一定相邻。
是顺序存取的结构。
这里的单链表都是带头结点的。

尾插法:
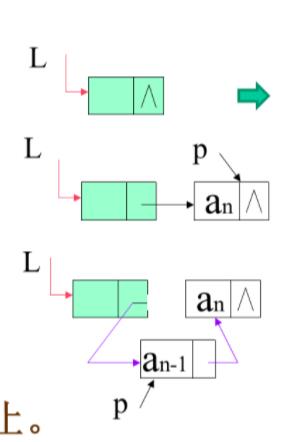
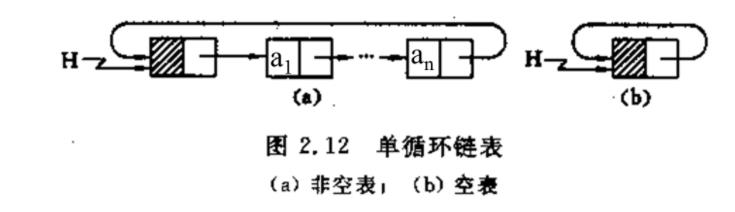
循环链表:
最后一个结点的指针域又指回头结点的链表。
双向链表:
插入删除都可以画这种图,就很容易知道指针的赋值变化了。
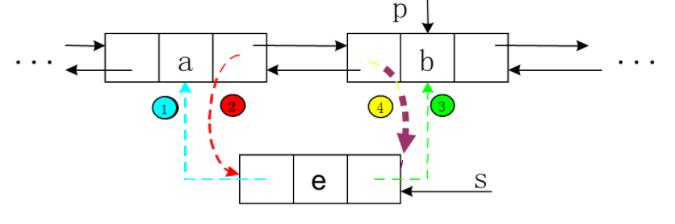
单链表总结和与线性表的比较

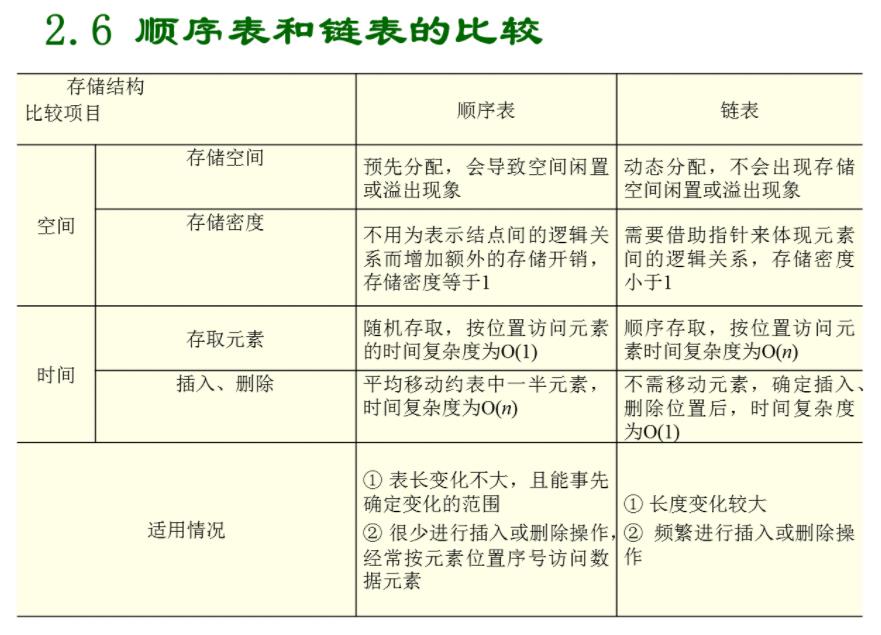
第三章
栈Stack,先进后出(像是电梯了),插入删除的一端为栈顶Top,另一端为底Bottom;
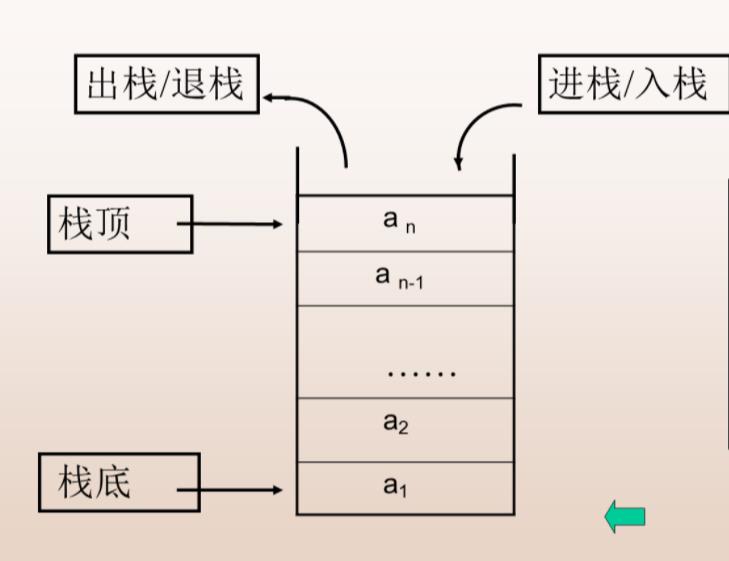
顺序栈
是利用顺序存储结构实现的栈,指针top指示栈顶在顺序栈的位置。
base为存储空间基地址,S.top-S.base 是栈中元素的个数,类似Length。
栈为空时:S.topS.base;
栈满时:S.top-S.baseMAXSIZE;
顺序栈,top在最高元素的上一个,base位置是最低元素,故取栈顶元素要取top-1的:
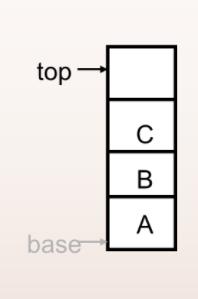
链栈
**没必要加头结点。**栈顶指针就是链表头指针。
关于阶乘的递归


队列
先进先出。头是front,尾是rear;
在非空队列中,头指针始终指向队头元素的位置(实位以在),尾指针指向队尾元素的下一个元素(虚位以待)。
队列为空时:Q.frontQ.rear;
初始化时都为0;
加入一个元素,Q.rear++;删去一个元素时,Q.front++;
队长:Q.rear-Q.front;
存在假上溢现象。
(Q.base是基地址)
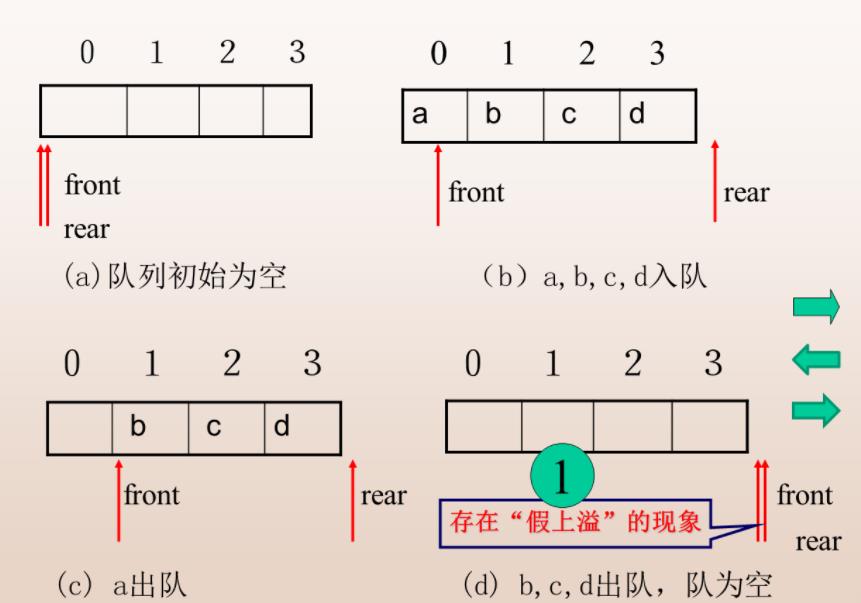
循环队列
队长:(Q.rear-Q.front+MAXSIZE)%MAXSIZE;
队满:Q.front(Q.rear+1)%MAXSIZE;
循环队列入队更新方式:
if((Q.rear+1)%MAXSIZE==Q.front) return ERROE;//满
Q.base[Q.rear]=e;//因为是虚位以待的
Q.rear=(Q.rear+1)%MAXSIZE;
出队:
if(Q.rear==Q.front) return ERROR;//空
e=Q.base[Q.front];
Q.front=(Q.front+1)%MAXSIZE;
第五章
重点:二叉树的遍历及其应用。
不特别说明,讨论的都是无序树。
树的层数:如图,4层。
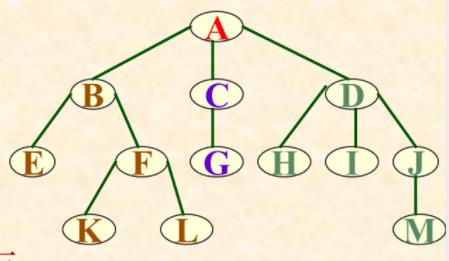
二叉树
五种基本形态:
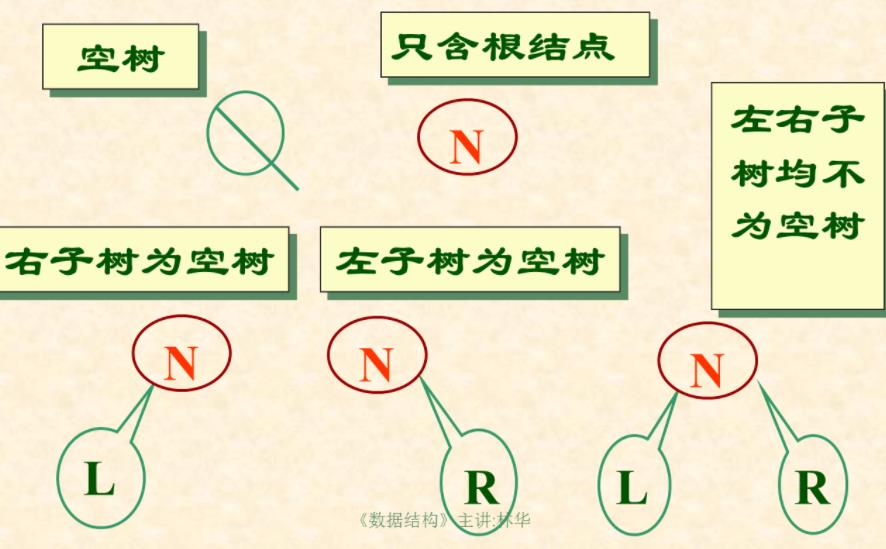
遍历二叉树
遍历:对数据结构中的每个元素都访问一次且只访问一次。
遍历的四种方法:
层次遍历:从上到下,从左到右
ABECFDGHK
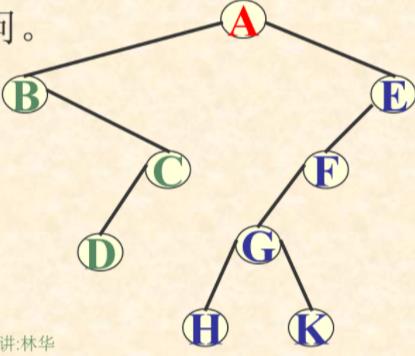
以下三个演示来自:数据结构——二叉树先序、中序、后序及层次四种遍历(C语言版)
先序遍历:根->左->右
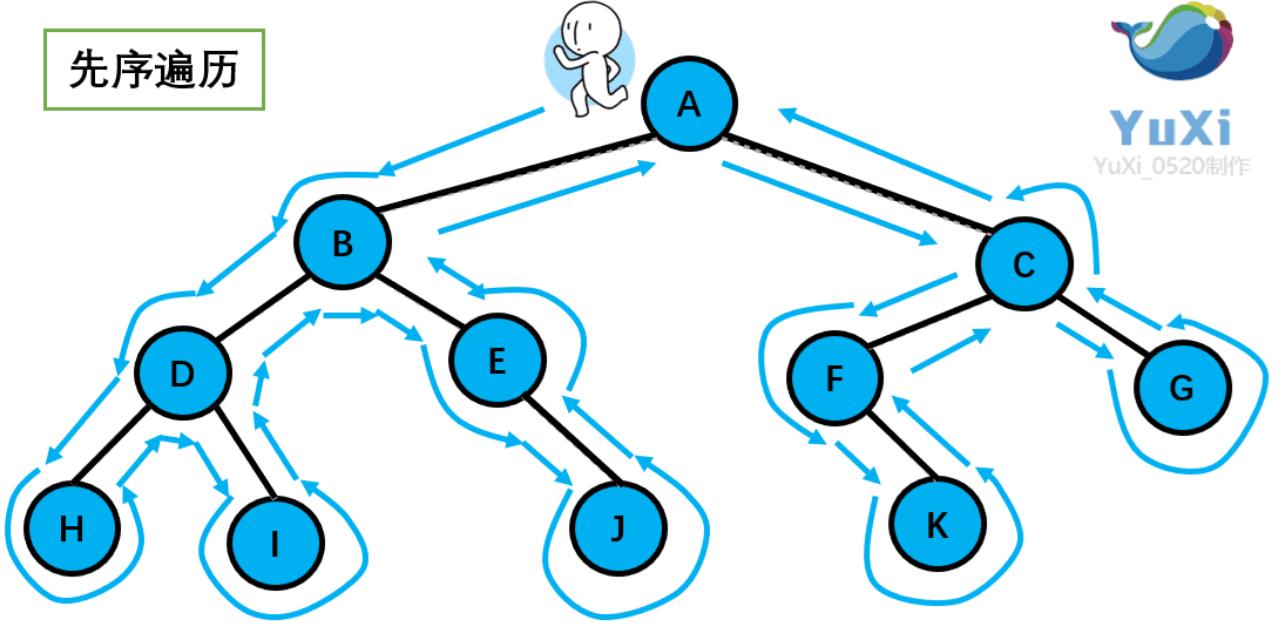
中序遍历:左->根->右
树上的结点都掉下来了
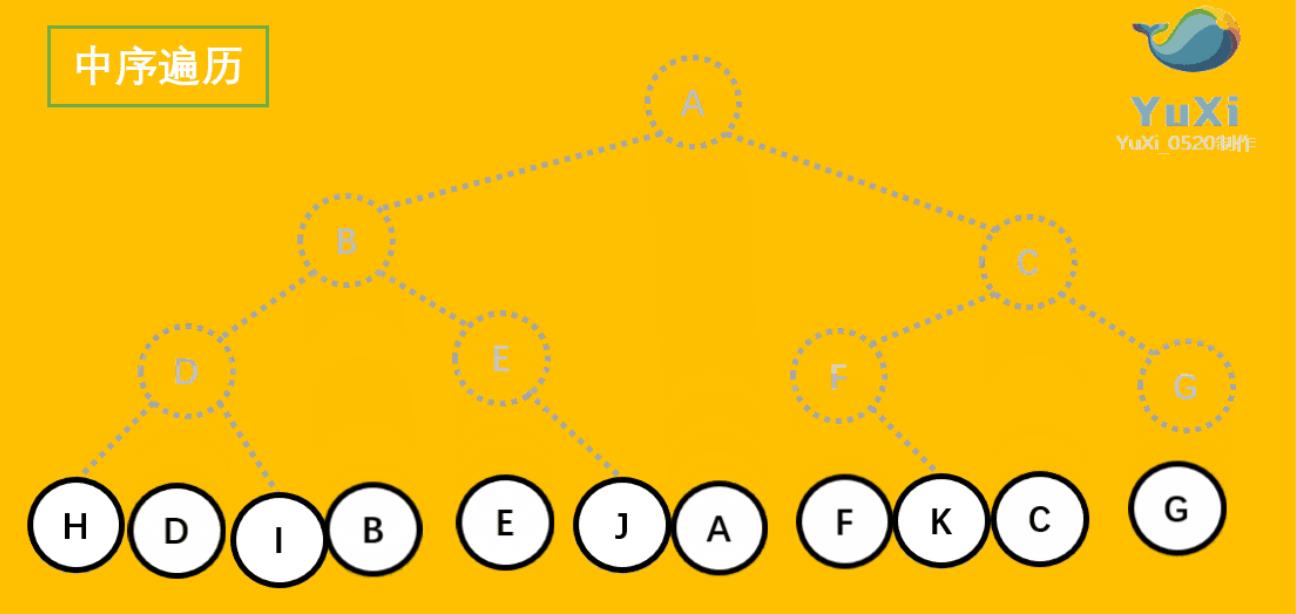
后序遍历:左->右->根
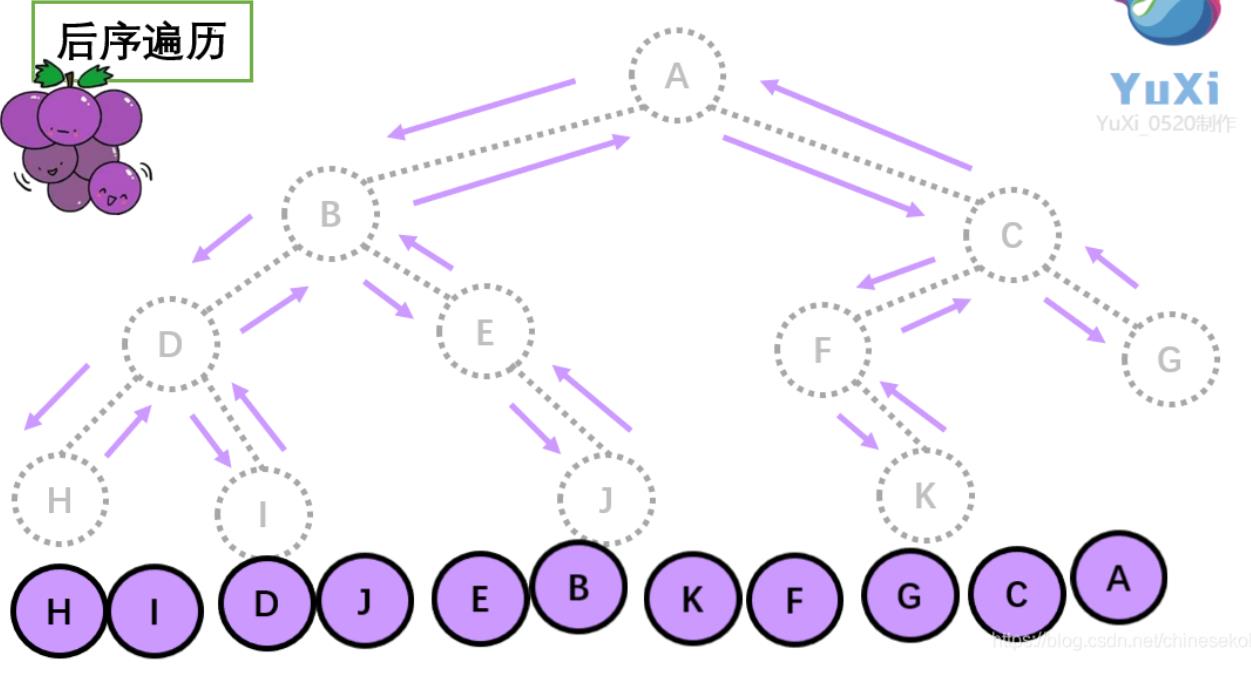
重要结论
若二叉树中的各结点的值均不同,则任意一颗二叉树的先、中、后序序列是唯一的。
先+中 或 后+中 可以唯一确定二叉树。

哈夫曼树
最优树,一类带权路径长度的最短树。
从这里学习WPL的计算方法:权值*路径长度(或者说这一层的层数) 之和。
易得:大的要近,小的要远,这样WPL就会最小。
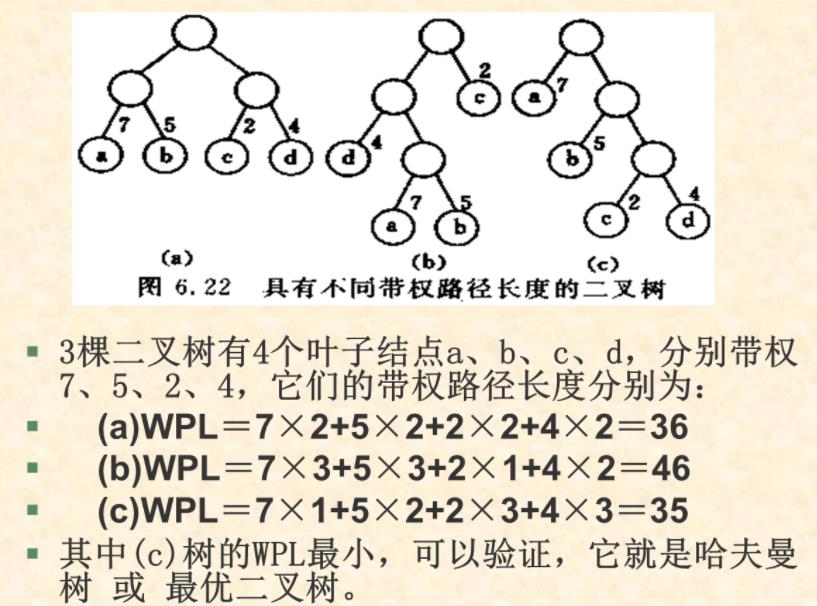
一个哈夫曼树的生成:
W={5,6,2,7,9};
先排序:W={2,5,6,7,9};
W={6,7,7,9};
W={7,13,9};
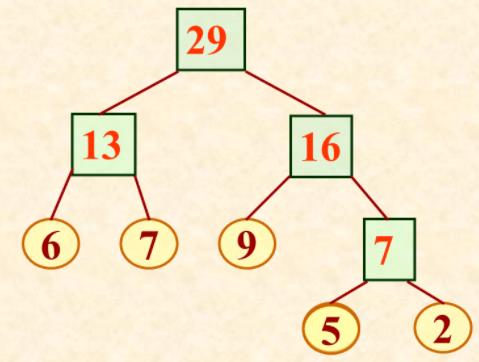
编码的两种形式
等长:易于译码。但长度长。
不等长:不易于译码,但长度短。
哈夫曼树是不等长的二进制编码,也是最优前缀编码。
如:
W={43,14,29,14};
左0右1:
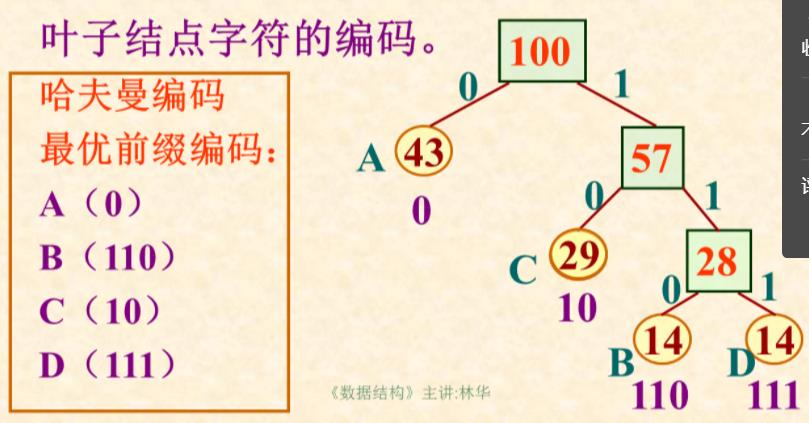
哈夫曼编码树中,若叶子结点个数为n,则总结点为2n-1。
第六章
重点:图的两种存储结构和构造算法,不同存储结构的特点和使用场合。
图的两种遍历算法:DFS,BFS。
图分为有向图和无向图。
有向完全图:n(n-1)
无向完全图:n(n-1)/2
稀疏图:边的个数小于nlog2n;
度:出度+入度(有向图);
简单路径:序列中顶点不重复出现的路径。
简单回路:除第一个和最后一个相同,其他不重复。
连通图:任意两个顶点之间联通。
强连通图:有向图中任意两个顶点之间都存在一条有向路径。
否则,它的各个极大强连通子图称为它的强连通分量。
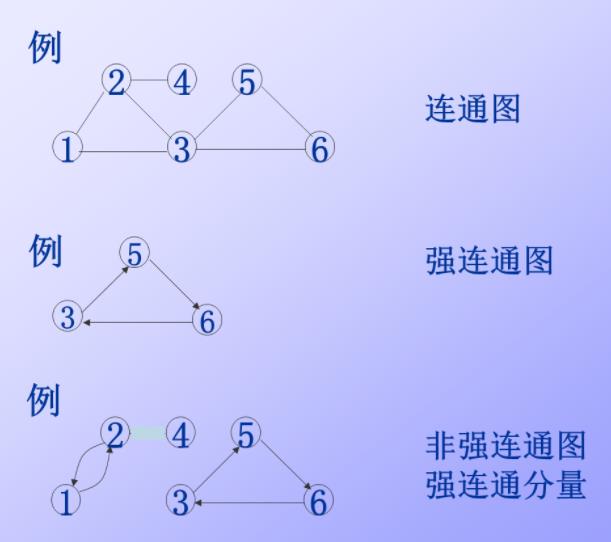
邻接矩阵
无向图的邻接矩阵为对称矩阵;
其实就是在有边的地方放1:
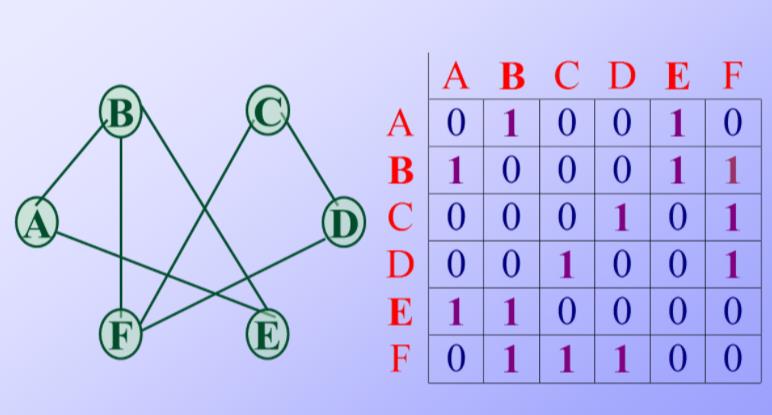
特点:
- 无向图的邻接矩阵对称,可压缩存储。这样,n个顶点的无向图需要的存储空间为n(n+1)/2;
- 便于计算各个顶点的度。顶点i的度为第i行元素为1的个数。
有向图的邻接矩阵:也是有边的地方1
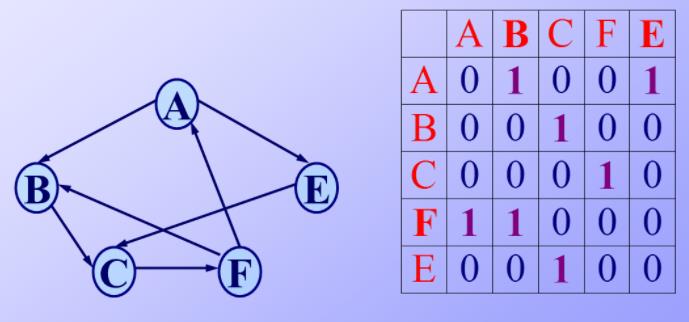
特点:
- n个顶点需要存储空间为n^2;
- 便于计算各顶点的度:第i行1的个数是i的出度;列——入度。
网的邻接矩阵
有边就放权值,否则为无穷大。

邻接矩阵的缺点
- 不便于增删结点
- 不便于统计边的数目,要扫描整个矩阵,时间复杂度为O(n^2)
- 对稀疏图很浪费空间
邻接表
连接的是出度,一般(地址)从小到大。
无向图:
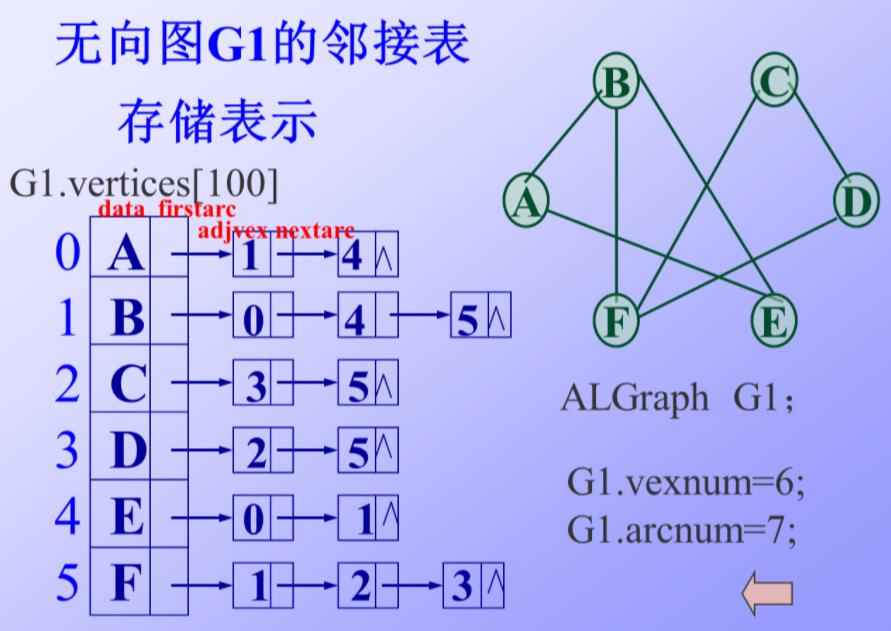
特点:
- 无向图中,每条边在邻接表中出现2次
- 空间复杂度O(n+2e),若是稀疏图,省空间
- 不唯一,因为链入顺序任意
- i的度为第i单链表中的结点数
有向图:
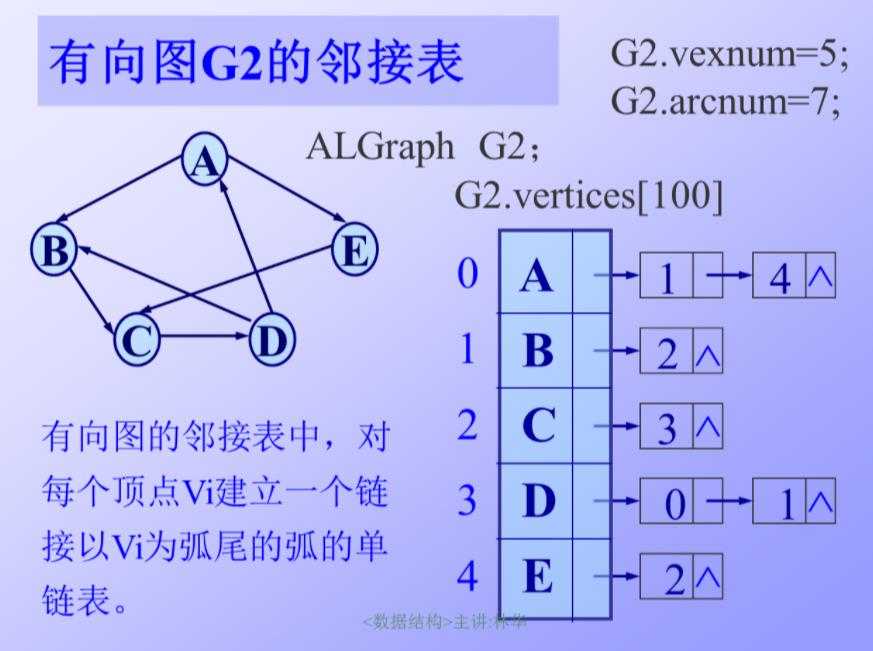
特点:
- 有向图中,一条弧在邻接表只出现一次;
- 空间复杂度O(n+e)
- i的度为第i单链表中的结点数
逆邻接表
连的是入度。
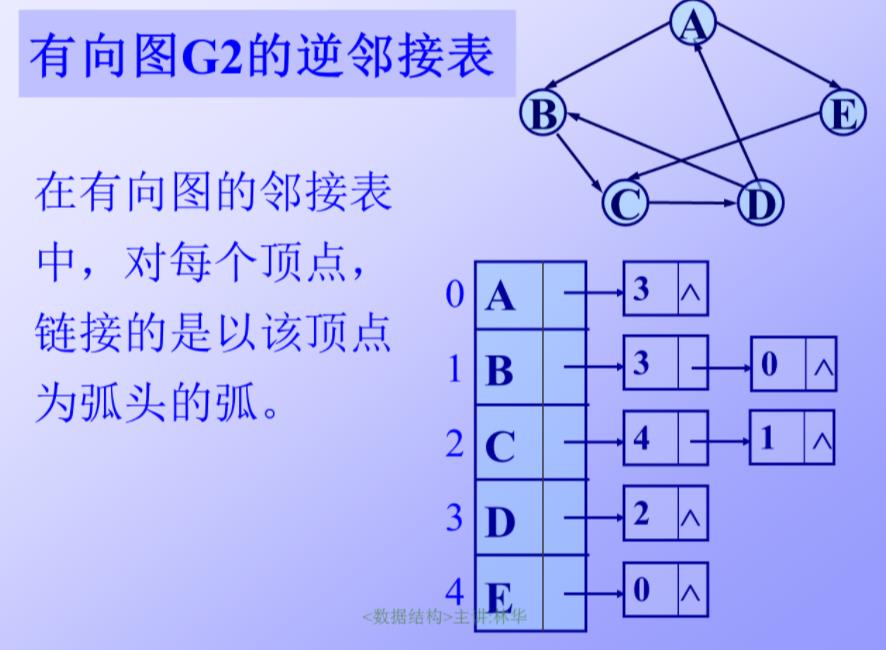
画网络
| 地址 | 权值 | 下一个指针 |
|---|
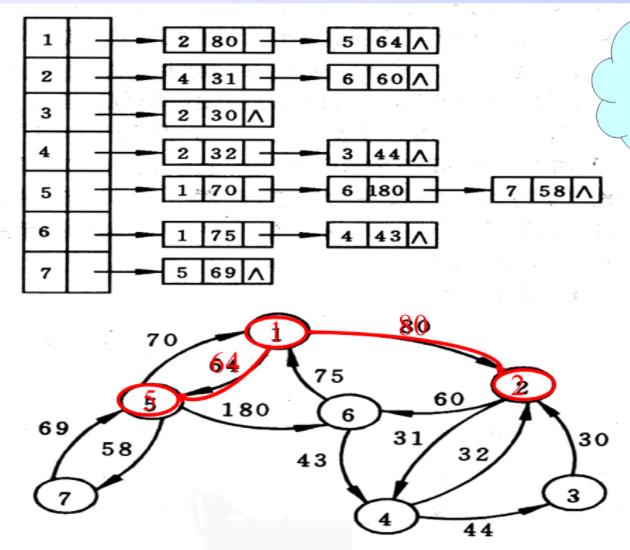
邻接表特点
- 便于增删
- 便于统计边的数目,扫描整个表即可,时间复杂度O(n+e)
- 不便于判断顶点之间是否有边
- 不便于计算各个顶点的度
- 通常,稠密图——邻接矩阵;稀疏图——邻接表
图的遍历:DFS和BFS
DFS:
访问顶点,若它的邻接点未被访问,则从它出发进行深搜:
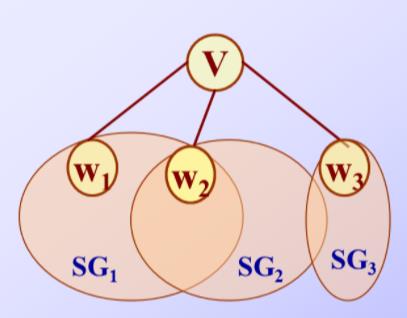
求DFS:
别拉太下,答案要出来啦!
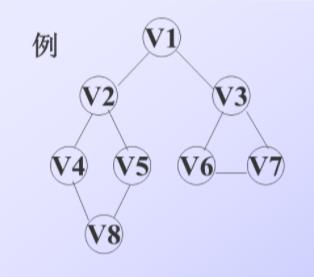
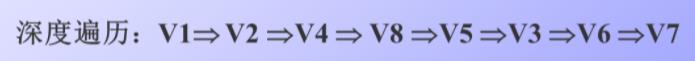
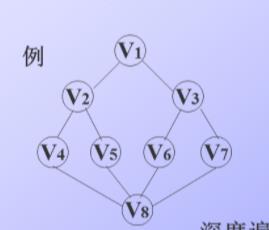

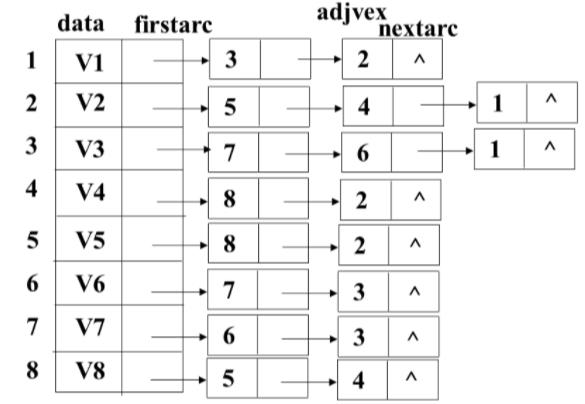
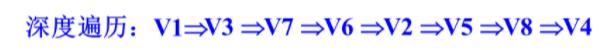
效率分析:
邻接矩阵O(n^2);适合稠密图。
邻接表O(n+e);稀疏图。
BFS:
用队列实现的一层层的,广度优先搜索。
从V0出发,依次访问V0的所有未被访问的邻接点,之后按它们被访问的先后次序访问它们的邻接点。
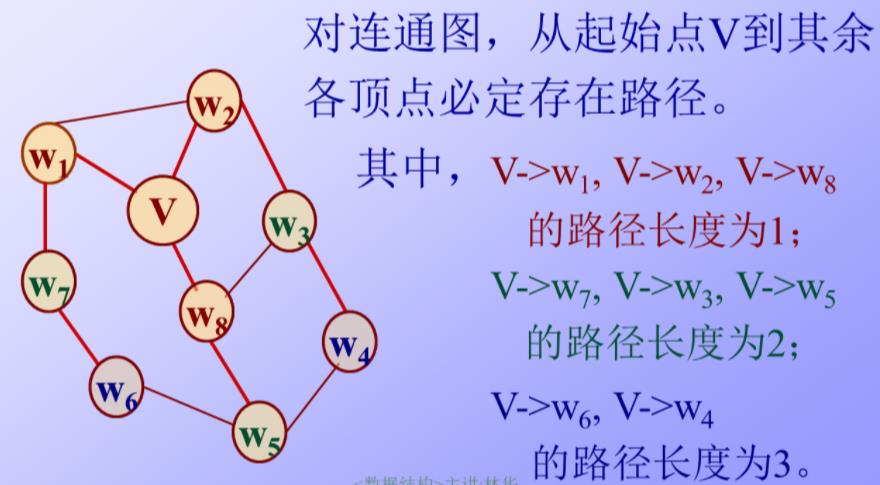
例题:
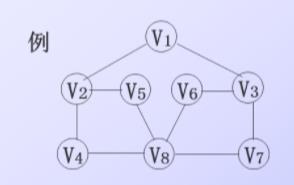
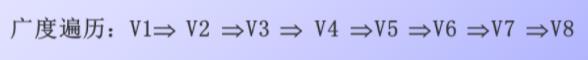
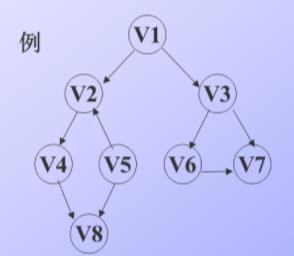

注意这里67都是3后的!
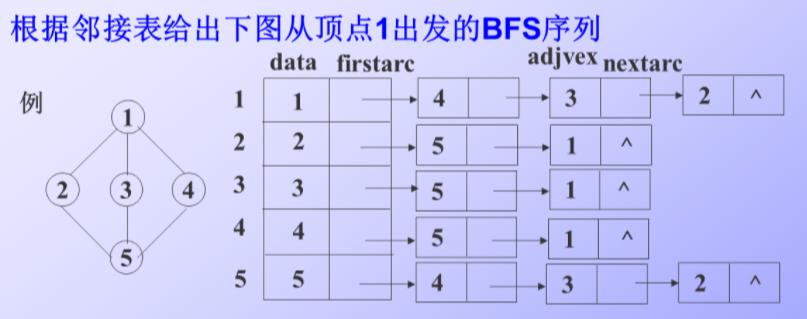
14325
效率分析:
邻接矩阵O(n^2);
邻接表O(n+e);
DFS VS BFS
- 空间复杂度相同,O(n);
- 时间复杂度与存储结构(邻接矩阵/邻接表)有关,与路径无关。
最小生成树
prim算法:
取图中任意一个顶点作为生成树的根,之后往生成树上添加新顶点w。在添加的顶点w和已经在生成树上的顶点v之间必定存在一条边,且该边的权值在所有连通vw的边中最小。
称为加点法。
克鲁斯卡尔算法:
以上是关于数据结构知识点总复习的主要内容,如果未能解决你的问题,请参考以下文章