数据结构——堆

Posted 2021-06-29 两片空白

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构——堆相关的知识，希望对你有一定的参考价值。

文章目录

前言
一.定义
三.重要操作
四.代码实现堆

前言

在现实生活中，我们处理事情时大多数情况下，我们并不是按照顺序，先来先处理的。许多情况下，我们会按照事情优先级来处理事情。比如：某个外科医生，某个患者受了点皮外伤，而排在他后面的患者受了很严重的外伤，这个医生肯定优先处理那个受了严重外伤的患者。下面介绍的堆正是考虑了这种特性的数据结构，通常堆也被称为“优先队列”。

一.定义

堆是一种特殊的队列，从堆中取出来的元素是按照元素优先级的大小，而不是元素进入队列的先后顺序。

表现形式：

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i =0，1，2…，则称为小堆(或大堆)。

性质：

堆是一颗完全二叉树
堆中某个节点的值总是不大于或不小于其父节点的。

由性质衍生出两种堆：

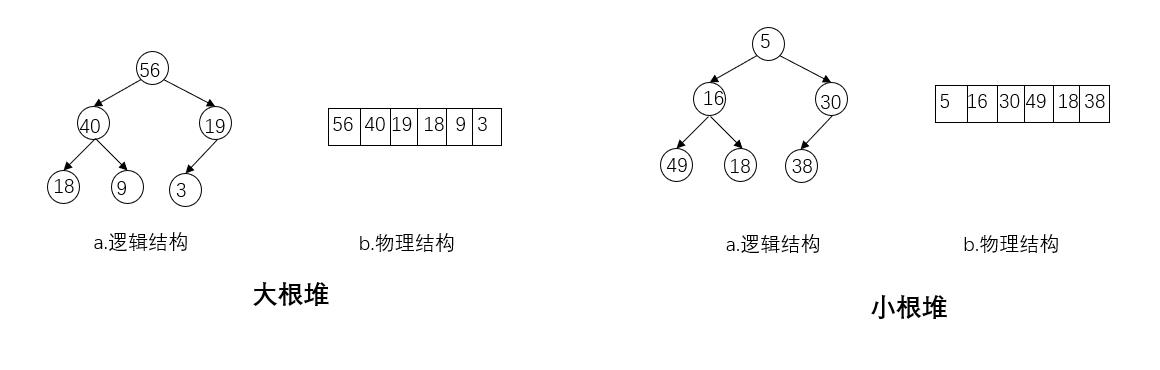
大根堆：左右子节点比父节点小
小根堆：左右子节点比父节点大。

下面两图就是堆：
在这里插入图片描述

三.重要操作

用一维线性数组来存储元素实现堆。堆信息与一些重要操作如下：
堆信息：

typedef int HDdatatype;
typedef struct Head{
	HDdatatype *a;
	int size;
	int capacity;

}HD;

1.向下调整堆

如果有一个二叉树，其左右子树都是堆，但是整体不是堆时(根节点不符合根的性质)
例如：int a[] = {27,15,19,18,28,34,65};左右子树位小根堆，就根节点不符合
如何调整：

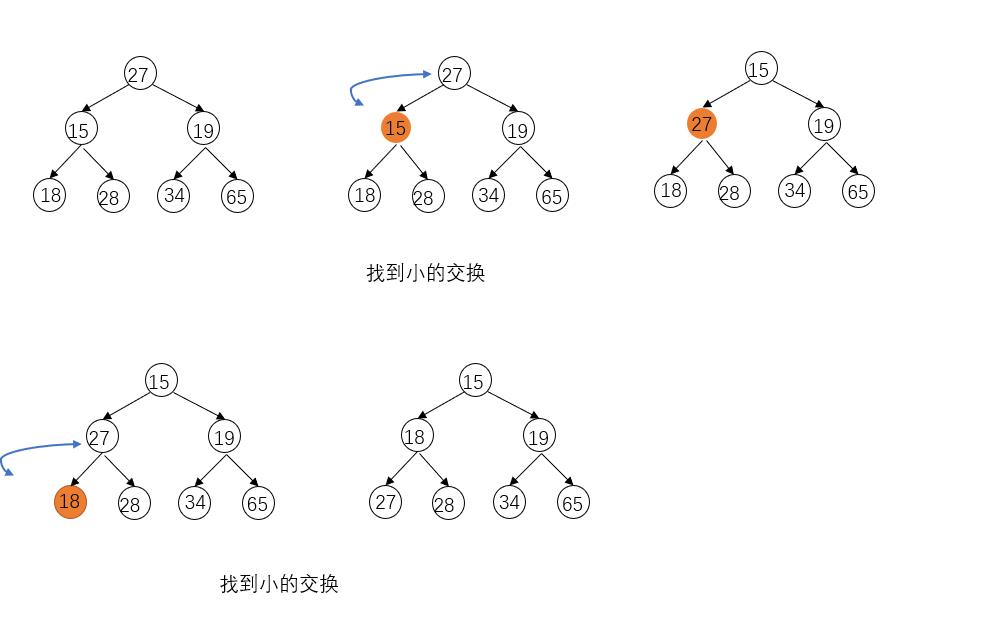
采用向下调整法：(小根堆)
找到左右子节点小的，跟父节点(要交换结点)比较
a.比父节点小，让子节点跟父节点交换。再以要交换结点作为父节点，找到左右子节点大的跟父节点比较，比父节点小交换。直到走到叶节点。
b.比父节点大，直接结束。

图示：
在这里插入图片描述

void Swap(int *px, int *py){
	int temp = *px;
	*px = *py;
	*py = temp;

}
//小根堆
static void AdjustDown(HDdatatype a[], int size, int parent){
	int child = parent * 2 + 1;//先假设左边的数比根数小
	while (child < size){//没有孩子结点退出
		if (child + 1 < size&&a[child] > a[child + 1]){//如果右边的数小，child++就得到右边数的下标
			child++;
		}
		if (a[child] < a[parent]){//如果孩子结点比父节点小就就交换
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else{//直到不大就退出
			break;
		}
	}
}

2.建立堆

如果有一个二叉树，其左右子树都不是堆，如何建立堆。
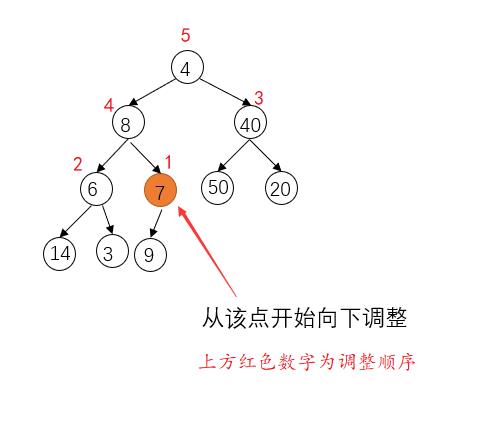
例如：int a[] = { 4, 8, 40,6,9,50,20 };完全无规律，没有一个结点符合堆的性质。
如何建立堆：
从数组下标最大的父节点开始调整,下标位 (n-1-1)/2,(n-1->数组最后一个元素再减1除以2就是最后一个结点的父节点)。
在这里插入图片描述

void HeadBuild(int a[],int num){
	for (int i = ((num - 1 - 1) / 2); i >= 0; i--){
		AdjustHead(a, num, i);
	}
}

3.插入

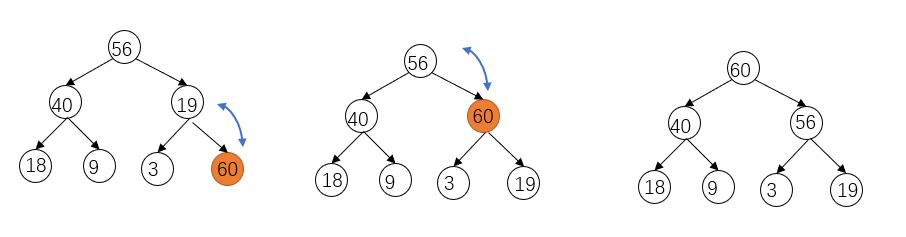
向上调整堆

当往一个堆里插入一个数据时，插入的位置为数组最后一个，这样可能会导致堆结构受到破坏，于是就需要向上去调整堆。
例如：
在这里插入图片描述

//大根堆
static void AdjustUp(HDdatatype a[], int child){//向上调整
	while (child > 0){//孩子节点等于0，没有父节点退出
		int parent = (child - 1) / 2;//得到父节点
		if (a[child]>a[parent]){//孩子节点比父节点大交换
			Swap(&a[child], &a[parent]);
			child = parent;
		}
		else{//直到不大退出
			break;
		}
	}
}

插入：

//在最后一个位置插入，再向上调整成堆
void HeadPush(HD *head, HDdatatype x){
	assert(head);
	if (HeadIsFull(head)){//堆满扩容
		HDdatatype *temp = (HDdatatype *)realloc(head->a, sizeof(HDdatatype)*head->capacity * 2);
		if (temp == NULL){
			printf("realloc fail\\n");
			HeadDestroy(head);
			exit(-1);
		}
		head->a = temp;
		head->capacity *= 2;
	}
	head->a[head->size] = x;
	head->size++;
	AdjustUp(head->a, head->size - 1);

}

4.删除

最大堆或者最小堆的删除实际是取出根节点最大值或者最小值元素，也就是第一个元素，同时删除它。
但是如果将第一个元素删除后用那个元素来做第一个元素呢？第二个？不行，以最大堆为例，因为我们并不知道第二个元素大还是低三个元素大。
我们的思路是假设堆的元素个数为N个。首先将第一个元素与最后一个元素交换，然后再将前面N-1元素向下调整，再删除最后一个元素即可。(这样交换只是首尾两个元素的堆性质被破坏，其它元素堆性质未被破坏，只需要进行向下交换即可)。

//假设有N各元素，将第一个元素(0)与最后一个元(N-1)素交换，再将前面N-1个元素向下调整成堆
HDdatatype HeadPop(HD *head){
	assert(head);
	int max = head->a[0];
	Swap(&head->a[0], &head->a[head->size - 1]);
	head->size--;
	AdjustDown(head->a, head->size - 1, 0);
	return max;
}

四.代码实现堆

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<Windows.h>
#include<assert.h>

typedef int HDdatatype;
typedef struct Head{
	HDdatatype *a;
	int size;
	int capacity;

}HD;

void HeadInit(HD *head, HDdatatype b[], int n);//堆初始化
void HeadDestroy(HD *head);//释放堆

void HeadPush(HD *head, HDdatatype x);//插入元素并保持堆的性质
HDdatatype HeadPop(HD *head);//弹出堆的首元素(优先级最高的）
HDdatatype HeadTop(HD *head);//得到堆的首元素

bool HeadIsEmpty(HD *head);//判断堆是否为空
bool HeadIsFull(HD *head);//判断堆是否满

int HeadSize(HD *head);//得到堆元素长度

void HeadPrint(HD *head);//打印堆元素

验证

#include"Head.h"

int main(){
	HDdatatype a[] = { 4, 8, 2, 6, 7, 15, 20, 9, 85, 75, 40 };
	int n = sizeof(a) / sizeof(a[0]);
	HD head;
	HeadInit(&head, a, n);
	HeadPrint(&head);
	HeadPush(&head, 13);
	HeadPrint(&head);
	HeadPush(&head, 90);
	HeadPrint(&head);

	HDdatatype max = HeadPop(&head);
	printf("%d\\n", max);
	HeadPrint(&head);


	system("pause");
	return 0;
}

函数定义

#include"Head.h"

static void Swap(int *px, int *py){
	int temp = *px;
	*px = *py;
	*py = temp;
}
//从下往上调整。得到大根堆
static void AdjustDown(HDdatatype a[], int size, int parent){
	int child = parent * 2 + 1;//先假设左边的数比根数大
	while (child < size){//没有孩子结点退出
		if (child + 1 < size&&a[child] < a[child + 1]){//如果右边的数大，child++就得到右边数的下标
			child++;
		}
		if (a[child] > a[parent]){//如果孩子结点比父节点大就就交换
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else{//直到不大就退出
			break;
		}
	}
}
static void AdjustUp(HDdatatype a[], int child){//向上调整
	while (child > 0){//孩子节点等于0，没有父节点退出
		int parent = (child - 1) / 2;//得到父节点
		if (a[child]>a[parent]){//孩子节点比父节点大交换
			Swap(&a[child], &a[parent]);
			child = parent;
		}
		else{//直到不大退出
			break;
		}
	}
}

//将数组b[]，调整成堆，
void HeadInit(HD *head, HDdatatype b[],int n){
	head->a = (HDdatatype *)malloc(sizeof(HDdatatype)*n);
	if (head->a == NULL){
		printf("malloc fail!\\n");
		exit(-1);
	}
	for (int i = 0; i < n; i++){
		head->a[i] = b[i];
	}
	head->size = n;
	head->capacity = n;

	for (int i=(head->size-1-1)/2;i>=0;i--)
	{
		AdjustDown(head->a, head->size, i);
	}
}

void HeadDestroy(HD *head){//释放
	free(head->a);
	head->a = NULL;
	head->capacity = 0;
	head->size = 0;
}
//在最后一个位置插入，再向上调整成堆
void HeadPush(HD *head, HDdatatype x){
	assert(head);
	if (HeadIsFull(head)){
		HDdatatype *temp = (HDdatatype *)realloc(head->a, sizeof(HDdatatype)*head->capacity * 2);
		if (temp == NULL){
			printf("realloc fail\\n");
			HeadDestroy(head);
			exit(-1);
		}
		head->a = temp;
		head->capacity *= 2;
	}
	head->a[head->size] = x;
	head->size++;
	AdjustUp(head->a, head->size - 1);

}

//假设有N各元素，将第一个元素(0)与最后一个元(N-1)素交换，再将前面N-1个元素向下调整成堆
HDdatatype HeadPop(HD *head){
	assert(head);
	int max = head->a[0];
	Swap(&head->a[0], &head->a[head->size - 1]);
	head->size--;
	AdjustDown(head->a, head->size - 1, 0);
	return max;
}

HDdatatype HeadTop(HD *head){
	assert(head);
	return head->a[0];
}

bool HeadIsEmpty(HD *head){
	if (head->size == 0){
		return true;
	}
	return false;
}

bool HeadIsFull(HD *head){
	if (head->size == head->capacity){
		return true;
	}
	return false;
}

int HeadSize(HD *head){
	assert(head);
	return head->size;
}

void HeadPrint(HD *head){
	for (int i = 0; i < head->size; i++){
		printf("%d ", head->a[i]);
	}
	printf("\\n");
}

以上是关于数据结构——堆的主要内容，如果未能解决你的问题，请参考以下文章

是否可以在 OnStop() 回收所有数据并使用保留片段？

算法排序之堆排序

是否可以在OnStop（）上回收所有数据并使用保留片段？

Rail片段缓存如何使您的应用受益，即阻止数据库调用？

方法与对象内存分析

VSCode自定义代码片段5——HTML元素结构