C++数据结构——二叉树

Posted 2021-06-29 eyes++

一：二叉树的储存结构

1.顺序存储：

用一组地址连续的存储单元，以层序顺序存放二叉树的数据结构元素，结点的相对位置蕴含着节点之间的关系。一般二叉树的顺序存储：把一般的二叉树先补成完全二叉树，然后按照完全二叉树的顺序存储方式进行存储，而新补上去的结点只占位置，不存放结点数据。可见非完全二叉树的顺序存储十分浪费空间

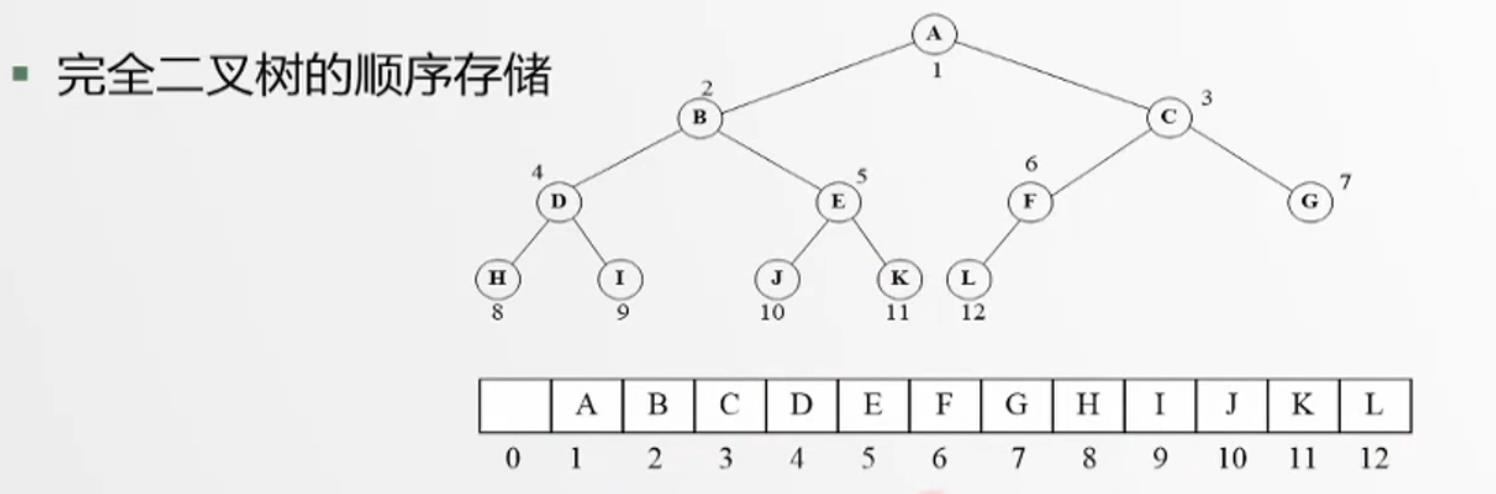
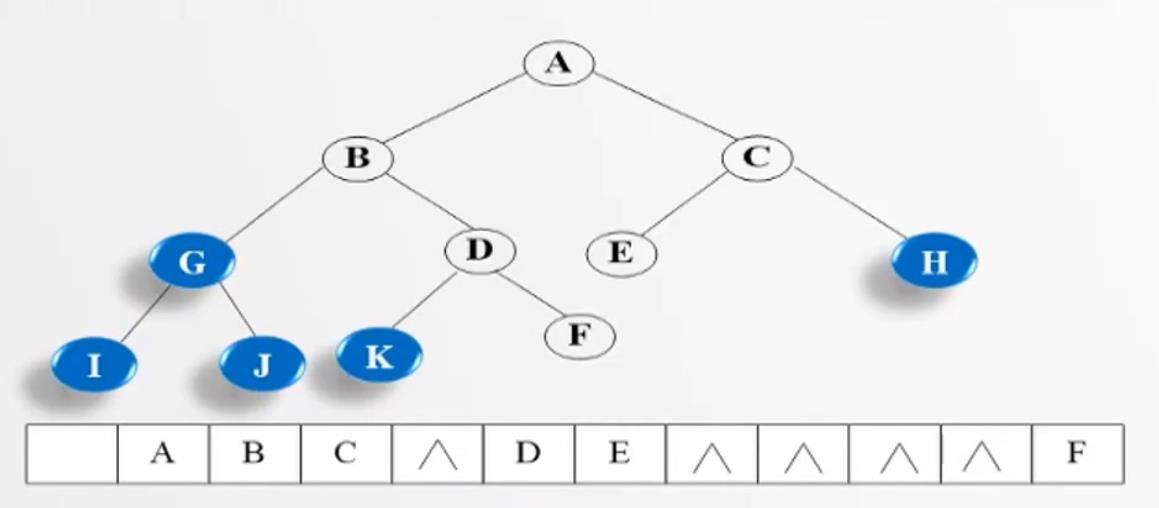
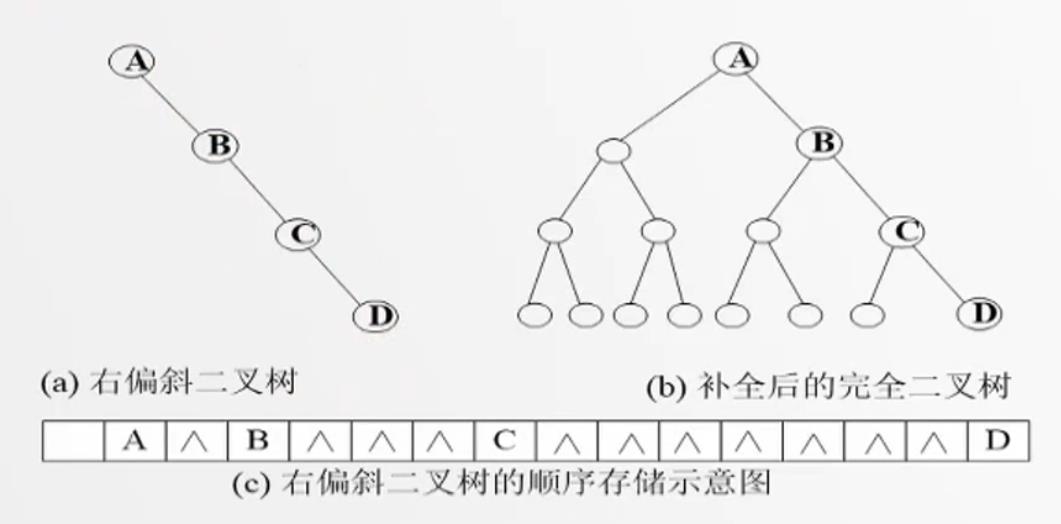
2.链式存储

二叉树链表：

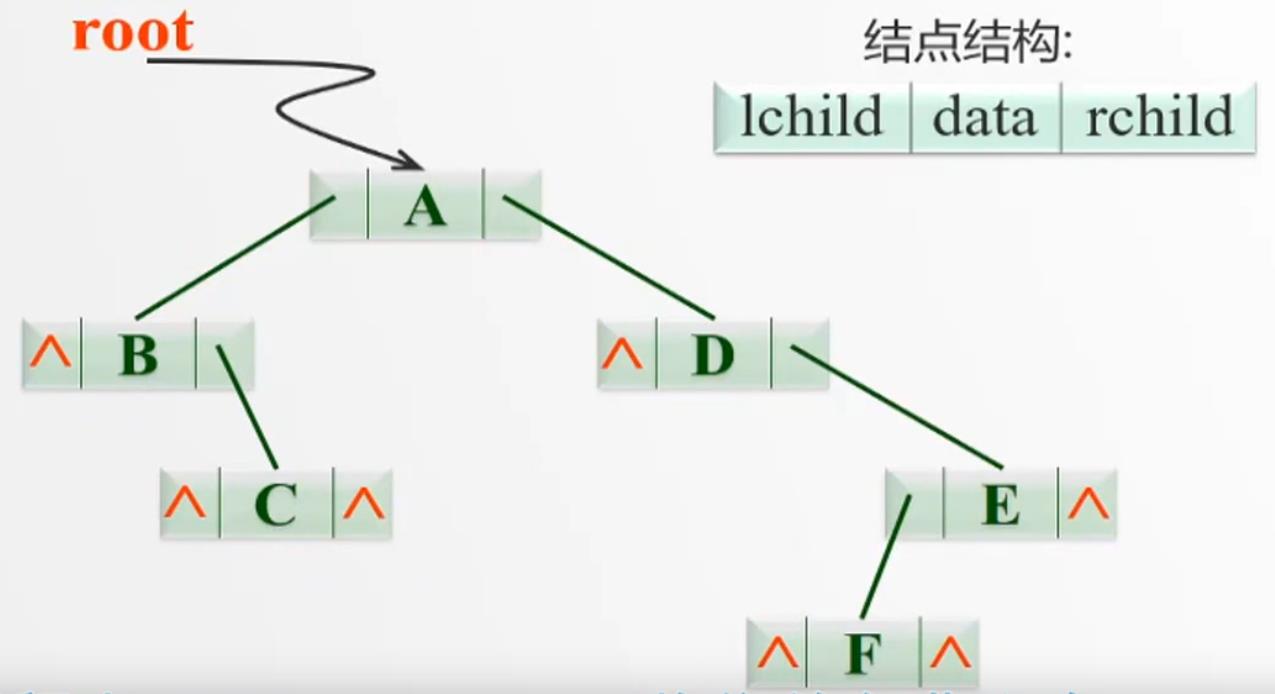对应的二叉链表结点结构：

struct bnode
{
	int data; // 不妨设数据类型为int
	bnode *lchild, *rchild;
};

四：二叉树的遍历

    问题的提出：顺着某一条搜索路径寻访二叉树的结点，使得每个结点均被访问且只被访问一次 
	递归遍历： 
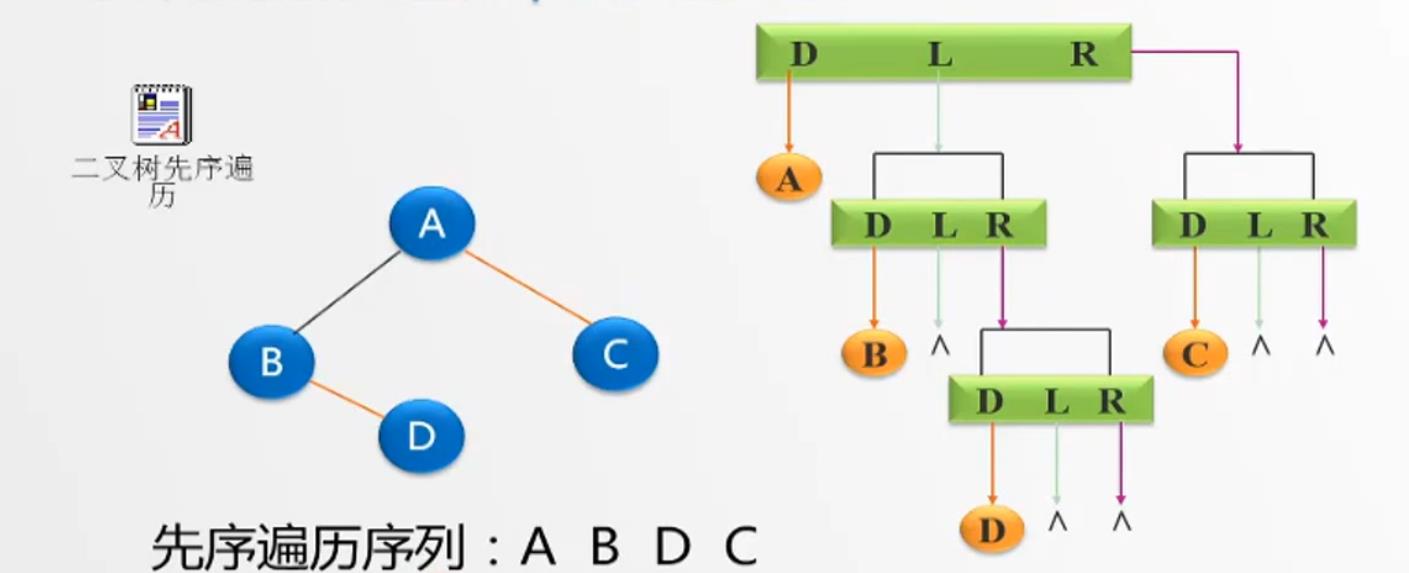
		    先序遍历算法： 
	            若二叉树非空，则 
		        1. 访问根节点
			    2. 先序遍历左子树
			    3. 先序遍历右子树
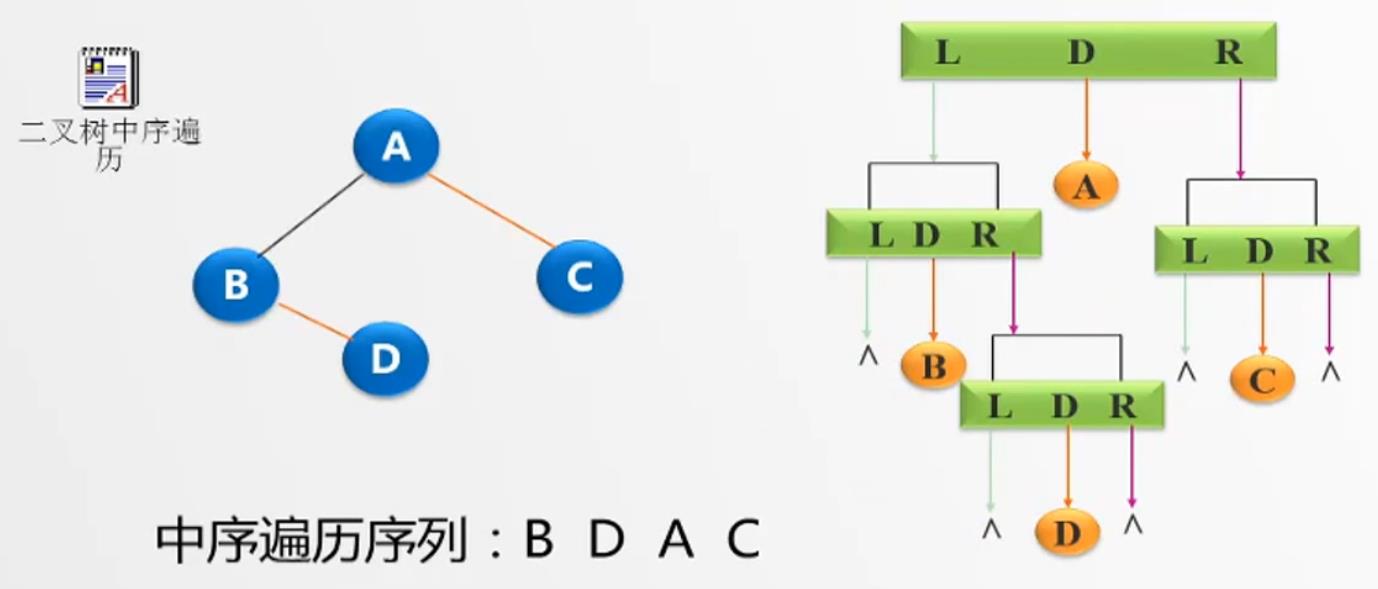
			中序遍历算法：
			 	若二叉树非空，则 
		        1. 中序遍历左子树 
			    2. 访问根结点 
			    3. 中序遍历右子树
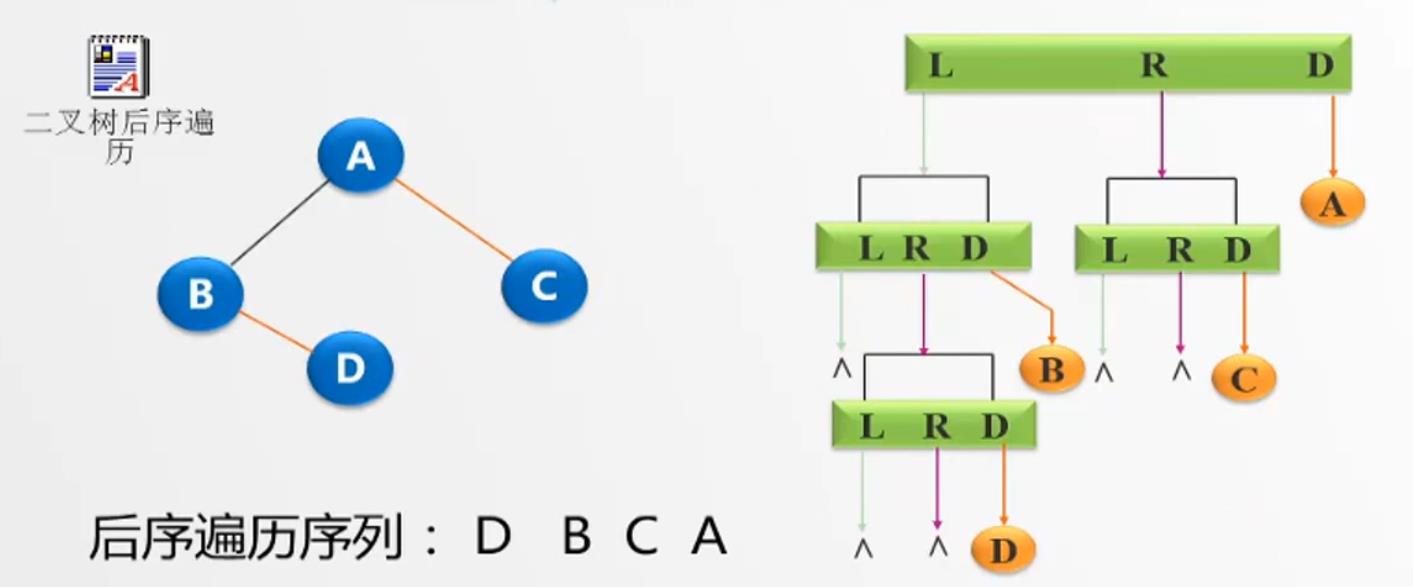
			后序遍历算法：
			 	若二叉树非空，则 
		        1. 后序遍历左子树 
			    2. 后序遍历右子树				
			    3. 访问根结点 

代码实现：

#include<iostream>
using namespace std;

struct bnode
{
	int data;
	bnode *lchild, *rchild;
};

class BiTree{
	public:
		BiTree();
		~BiTree();
		void createTree(); // 创建二叉树(插入构造)
		void visite(bnode* T); // 访问根结点 
		bnode* getroot(); // 拿到根结点 
		void insertNode(int ele); // 插入结点(按大小插入)
		void preorder(); // 前序遍历树
		void inorder(); // 中序遍历树
		void postorder(); // 后序遍历树
		int nodeNum(); // 获得结点总数 
		int treeH(); // 获得树的高度

		void degree2(); // 案例：按中序遍历输出二叉树中度为2的结点的值 
	private:
		bnode* root; // 根指针
		int count; // 结点个数
		int height; // 树的高度 
		void preorder(bnode* T); 
		void inorder(bnode* T); 
		void postorder(bnode* T);
		int nodeNum(bnode* T);
		int treeH(bnode* T);
		void degree2(bnode* T);
};

BiTree::BiTree(){
    root = NULL;
}

BiTree::~BiTree(){
	
}

void BiTree::createTree(){
	int n;
	cout << "计划插入结点数：";
	cin >> n;
	cout << "请输入树结点：";
	for(int i = 0; i < n; i++) // 输入n个数并创建这个树 
	{
		int ele;
		cin >> ele;
		insertNode(ele); 
	}
}

void BiTree::visite(bnode* T){
	cout << T->data << "  ";
}

bnode* BiTree::getroot(){
	return root;
}

void BiTree::insertNode(int ele){
	bnode* t = new bnode;
	t->data = ele;
	t->lchild = NULL;
	t->rchild = NULL;
	if(root == NULL) // 是空树就直接放在根下
	    root = t;
	else{
		bnode* temp = root;
		while(temp != NULL)
		{
			if(ele < temp->data)
			{
				if(temp->lchild == NULL)
				{
					temp->lchild = t;
					break;
				}
				else
				    temp = temp->lchild;
			}
			else
			{
				if(temp->rchild == NULL)
				{
					temp->rchild = t;
					break;
				}
				else
				    temp = temp->rchild;
			}
		}
	}
}

void BiTree::preorder(){ // 先序遍历当前二叉树算法，public成员函数 
	preorder(root);
}
void BiTree::preorder(bnode* T){ // 先序遍历以 T 为根指针的二叉树算法 
	if(T != NULL)
	{
		visite(T); // 访问 T 的节点数据 
		preorder(T->lchild); // 先序遍历 T 的左子树 
		preorder(T->rchild);  // 先序遍历 T 的右子树 
	}
}

void BiTree::inorder(){
	inorder(root);
}
void BiTree::inorder(bnode* T){
	if(T != NULL)
	{
		inorder(T->lchild);
		visite(T);
		inorder(T->rchild);
	}
}

void BiTree::postorder(){
	postorder(root);
}
void BiTree::postorder(bnode* T){
	if(T != NULL)
	{
		postorder(T->lchild);
		postorder(T->rchild);
		visite(T);
	}
}

int BiTree::nodeNum(){
    count = 0;
	return nodeNum(root);
}
int BiTree::nodeNum(bnode* T){
	if(T == NULL)
	    return 0;
	else
	{
	    nodeNum(T->lchild);
	    nodeNum(T->rchild);
	    count++;
		return count;		
	}
}

int BiTree::treeH(){
	return treeH(root);
}
int BiTree::treeH(bnode* T){
	if(T == NULL)
	    return 0;
	else
		return max(treeH(T->lchild), treeH(T->rchild)) + 1;
}

void BiTree::degree2(){
	degree2(root);
}
void BiTree::degree2(bnode* T){
	if(T != NULL)
	{
		degree2(T->lchild);
		if(T->lchild != NULL && T->rchild != NULL)
		    cout << T->data << endl;
		degree2(T->rchild);		
	}
}

int main()
{
	BiTree tr;
	tr.createTree();
	tr.preorder();
	cout << endl;
	tr.inorder();
	cout << endl;
	tr.postorder();
	cout << endl;
	cout << tr.nodeNum() << endl;
    cout << tr.treeH() << endl;
    tr.degree2();
	return 0;
}