第九章罚函数法

Posted 2021-06-29 是璇子鸭

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了第九章罚函数法相关的知识，希望对你有一定的参考价值。

内容来自马昌凤编著的《最优化方法及其Matlab程序设计》，文章仅为个人的学习笔记，感兴趣的朋友详见原书。

罚函数法的基本思想：根据约束条件的特点，将其转化为某种惩罚函数加到目标函数中去，从而将约束优化问题转化为一系列的无约束优化问题来求解。

1.外罚函数法

算法

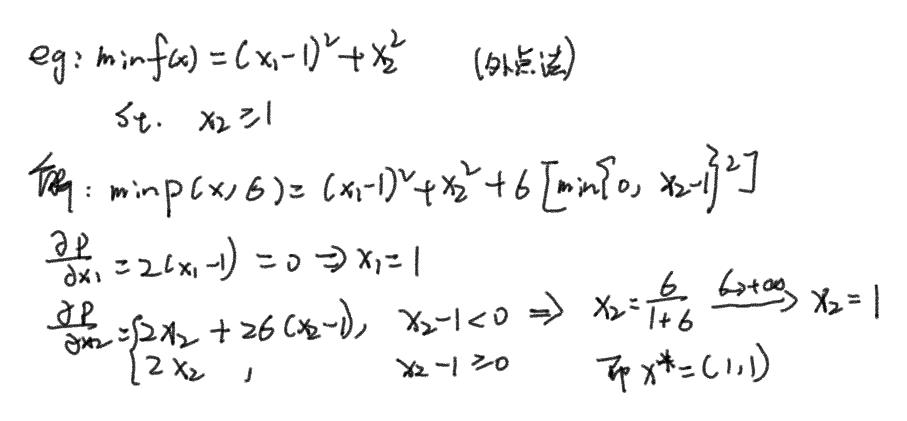
在这里插入图片描述

示例

在这里插入图片描述

2.内点法

内点法仅适用于不等式约束的优化问题
$min f(x), x∈R^n$
$s.t. g_i(x)≥0, i=1,...,m$

基本思想：保持每一个迭代点 $x_k$ 都是可行域 $D$ 的内点，可行域的边界被筑起一道很高的“围墙”作为障碍，当迭代点靠近边界时，增广目标函数值骤然增大，以示“惩罚”，并阻止迭代点穿越边界。

算法

在这里插入图片描述

示例

在这里插入图片描述
故对一般约束问题的内点法，等式约束利用“外罚函数”的思想，而不等式约束则利用“障碍函数”的思想构造出混合增广目标函数。

3.乘子法

基本思想：从原问题的拉格朗日函数出发，再加上适当的罚函数，从而将原问题转化为求解一系列的无约束优化子问题

等式约束问题的乘子法

在这里插入图片描述

不等式约束问题的乘子法

为等式约束的推广，即先引进辅助变量把不等式约束化为等式约束，再利用最优性条件消去辅助变量。
在这里插入图片描述

在这里插入图片描述

程序

增广拉格朗日函数

function psi=mpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma)
f=feval(fun,x);  he=feval(hf,x);  gi=feval(gf,x);
l=length(he); m=length(gi);
psi=f;  s1=0.0;
for(i=1:l)
    psi=psi-he(i)*mu(i);
    s1=s1+he(i)^2;
end
psi=psi+0.5*sigma*s1;
s2=0.0;
for(i=1:m)
    s3=max(0.0, lambda(i) - sigma*gi(i));
    s2=s2+s3^2-lambda(i)^2;
end
psi=psi+s2/(2.0*sigma);

增广拉格朗日函数的梯度

function dpsi=dmpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma)
dpsi=feval(dfun,x);
he=feval(hf,x);  gi=feval(gf,x);
dhe=feval(dhf,x);  dgi=feval(dgf,x);
l=length(he); m=length(gi);
for(i=1:l)
    dpsi=dpsi+(sigma*he(i)-mu(i))*dhe(:,i);
end
for(i=1:m)
    dpsi=dpsi+(sigma*gi(i)-lambda(i))*dgi(:,i);
end

乘子法程序

function [x,mu,lambda,output]=multphr(fun,hf,gf,dfun,dhf,dgf,x0)
% 功能: 用乘子法解一般约束问题:  min f(x), s.t. h(x)=0, g(x)>=0
%输入:  x0是初始点, fun, dfun分别是目标函数及其梯度；
%   hf, dhf分别是等式约束（向量）函数及其Jacobi矩阵的转置；
%   gf, dgf分别是不等式约束（向量）函数及其Jacobi矩阵的转置；
%输出:  x是近似最优点，mu, lambda分别是相应于等式约束和不
%   等式约束的乘子向量；output是结构变量，输出近似极小值f, 迭
%   代次数
maxk=500;   %最大迭代次数
sigma=2.0;  %罚因子
eta=2.0;  theta=0.8;  %PHR算法中的实参数
k=0; ink=0;  %k, ink分别是外迭代和内迭代次数
epsilon=1e-5;  %终止误差值
x=x0;  he=feval(hf,x); gi=feval(gf,x);
n=length(x); l=length(he); m=length(gi);
%选取乘子向量的初始值
mu=0.1*ones(l,1);  lambda=0.1*ones(m,1);
btak=10;  btaold=10;  %用来检验终止条件的两个值
while(btak>epsilon & k<maxk)
    %调用BFGS算法程序求解无约束子问题
    [x,ival,ik]=bfgs('mpsi','dmpsi',x0,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma);
    ink=ink+ik; 
    he=feval(hf,x); gi=feval(gf,x);
    btak=0.0;
    for (i=1:l), btak=btak+he(i)^2;   end
    for i=1:m
        temp=min(gi(i),lambda(i)/sigma);
        btak=btak+temp^2;
    end
    btak=sqrt(btak);   
    if btak>epsilon
        if(k>=2 & btak > theta*btaold)
            sigma=eta*sigma;
        end
        %更新乘子向量
        for (i=1:l),  mu(i)=mu(i)-sigma*he(i);  end
        for (i=1:m)
            lambda(i)=max(0.0,lambda(i)-sigma*gi(i));
        end
    end
    k=k+1;
    btaold=btak;
    x0=x;
end
f=feval(fun,x);
output.fval=f;
output.iter=k;
output.inner_iter=ink;
output.bta=btak;
%xstar=[0.5*(sqrt(7)-1);0.25*(sqrt(7)+1)];
%err1=norm(x-xstar)