第四章 共轭梯度法

Posted 2021-06-29 是璇子鸭

内容来自马昌凤编著的《最优化方法及其Matlab程序设计》，文章仅为个人的学习笔记，感兴趣的朋友详见原书。

共轭梯度法是介于最速下降法与牛顿法之间的一种无约束优化算法，具有超线性收敛速度，算法结构简单。同时，与前一章的最速下降法类似，共轭梯度法只用了目标函数及其梯度值，避免了求二阶导数，从而降低了计算和储存量。

共轭方向法

共轭的定义

设G是n阶对称正定矩阵，若n维向量组$d_1,d_2,...,d_m(m<=n)$满足：
$d_i^{T}G{d}_j=0,i\ne j$
则称$d_1,d_2,...,d_m$为G共轭的。

对称正定矩阵$G$的共轭向量组必然是线性无关的

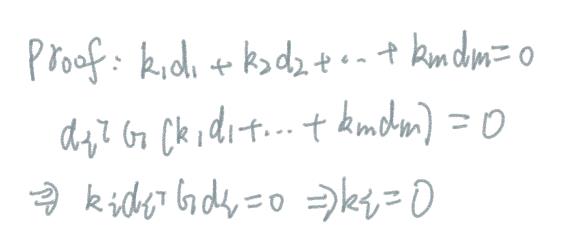
算法

共轭梯度法

算法

程序

function [x,val,k]=frcg(fun,gfun,x0)
% 功能: 用FR共轭梯度法求解无约束问题:  min f(x)
%输入:  x0是初始点, fun, gfun分别是目标函数和梯度
%输出:  x, val分别是近似最优点和最优值,  k是迭代次数.
maxk=5000;   %最大迭代次数
rho=0.6;sigma=0.4;
k=0;  epsilon=1e-4; 
n=length(x0);
while(k<maxk)
    g=feval(gfun,x0);  %计算梯度
    itern=k-(n+1)*floor(k/(n+1));
    itern=itern+1;
    %计算搜索方向
    if(itern==1)  
        d=-g;  
    else
        beta=(g'*g)/(g0'*g0);
        d=-g+beta*d0;  gd=g'*d;
        if(gd>=0.0)
            d=-g;  
        end
    end
    if(norm(g)<epsilon), break; end   %检验终止条件
    m=0; mk=0;
    while(m<20)   %Armijo搜索
        if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d)
            mk=m; break;
        end
        m=m+1;
    end
    x0=x0+rho^mk*d;
    val=feval(fun,x0);
    g0=g;  d0=d; 
    k=k+1;
end
x=x0;
val=feval(fun,x); 

示例1

示例2