8.15 SNAIL:神经注意力元学习
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了8.15 SNAIL:神经注意力元学习相关的知识,希望对你有一定的参考价值。
8.7 Meta learning元学习全面理解、MAML、Reptile
论文:A SIMPLE NEURAL ATTENTIVE META-LEARNER
元学习可以被定义为一种序列到序列的问题;在现存的方法中,元学习器的瓶颈是如何去吸收同化利用过去的经验。注意力机制可以允许在历史中精准摘取某段具体的信息。
SNAIL 组合时序卷积和 self- attention ;前者是去从过去的经验整合信息,后者是去精确查找到某些特殊的信息。
1、前言
许多方法也将元学习器看作是一个传统学习器的更新方法。例如元学习器使用 LSTM进行梯度优化,元学习器学到的策略能够被解释为一种基于梯度的优化算法
Ravi & Larochelle 扩展了这个方法,在一个少样本分类任务中使用一个相似的 LSTM 元学习器,这里传统的学习器(主学习器)是一个基于 CNN 的分类器。这里元学习算法被分解为两部分:传统学习器的初始参数被训练去适应快速的基于梯度的调整;LSTM 元学习器被训练去用于元学习任务的优化。Finn et al. 研究了一种特殊的情景,即 MAML。
所有这些方法都有领域独立的优点,但是他们显式的编码了元学习器需要去遵守的某些**特定的策略。**在一个特定的领域,可能存在更好的策略去利用任务的结构,但是基于梯度的方法将不再能解决这个。相反的,SNAIL 提出的方法中一个泛化的结构有能力去学习一个可以利用领域特殊化任务结构的算法。
时序卷积(TCN)有因果前后关系的,即在下一时间步生成的值仅仅受之前的时间步影响.但是,随着序列长度的增加,卷积膨胀的尺度会随之指数增加,需要的层数也会随之对数增加。因此这种方法对于之前输入的访问更粗略,且他们的有限的能力和位置依赖并不适合元学习器,因为元学习器应该能够利用增长数量的经验,而不是随着经验的增加,性能会被受限。
self-attention 可以实现从超长的序列内容中获取准确的特殊信息。它将 context 作为一种无序的 key-value 存储,这样就可以基于每个元素的内容进行查询。但是,位置依赖的缺乏(因为是无序的)也是一个缺点,文本是呈序列的。
2、SNAIL网络
我们使用一些主要的构建块来组成SNAIL架构。对于每一个模块的输入 ,大小为: ( 序 列 长 度 × 输 入 特 征 维 数 ) (序列长度 \\times 输入特征维数) (序列长度×输入特征维数) .为了提高深层卷积体系结构的容量和加速训练,使用了一些已有的技术手段:批规范化、残差连接、密集连接。这些技术极大地提高了SNAIL的表达能力和训练速度。下面具体说明几个模块:
时序卷积网络
👉2.4时序卷积网络TCN:因果膨胀卷积、残差连接和跳过连接
因果膨胀卷积:

图
1
图1
图1
tf.pad(tensor, paddings, mode="CONSTANT", constant_values=0, name=None)
这个操作根据你指定的’ padding ‘填充’张量’。’ paddings ‘是一个形状为’ [n, 2] ‘的整数张量,其中n为’张量’的秩。对于’ input '的每个维度D, ’ paddings[D, 0] ‘表示在该维度’张量’的内容之前添加多少值,而’ paddings[D, 1] '表示在该维度’张量’的内容之后添加多少值。
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings1 = tf.constant([[1, 0,], [2, 2]])
paddings2 = tf.constant([[0, 1, ], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
print(tf.pad(t, paddings1, "CONSTANT"))
print(tf.pad(t, paddings2, "CONSTANT"))
tf.Tensor(
[[0 0 0 0 0 0 0]
[0 0 1 2 3 0 0]
[0 0 4 5 6 0 0]], shape=(3, 7), dtype=int32)
tf.Tensor(
[[0 0 1 2 3 0 0]
[0 0 4 5 6 0 0]
[0 0 0 0 0 0 0]], shape=(3, 7), dtype=int32)
Process finished with exit code 0
因果膨胀卷积实现:
class CasualConv1d(Layer):
def __init__(self, filters,
kernel_size,
strides=1,
dilation_rate=1,
causal=True,
kernel_initializer='glorot_uniform',
name=None):
super(CasualConv1d, self).__init__(name=name)
self.filters = filters
self.kernel_size = kernel_size
self.strides = strides
self.dilation_rate = dilation_rate
self.causal = causal
self.activation = activations.get(activation)
self.kernel_initializer = initializers.get(kernel_initializer)
def build(self, input_shape): # Create the weights
self.Conv1D = Conv1D(filters = self.filters,
kernel_size = self.kernel_size,
kernel_initializer = self.kernel_initializer,
padding = 'valid',
dilation_rate = self.dilation_rate,
activation = self.activation
)
super(CasualConv1d, self).build(input_shape)
def call(self, input):
# input:[batch_shape ,steps, input_dim]
if self.causal:
padding_size = (self.kernel_size - 1) * self.dilation_rate
# padding: 1st dim is batch, so [0,0]; 2nd dim is time, so [padding_size, 0]; 3rd dim is feature [0,0]
input = tf.pad(input, [[0, 0], [padding_size, 0], [0, 0]])
output = self.Conv1D(input)
return output
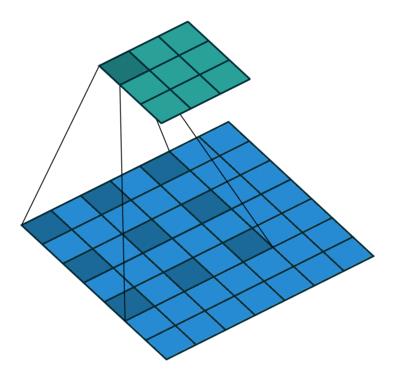
- dilation_rate为膨胀系数(如上图1所示,也就是卷积核元素之间的距离),steps为要处理的序列长度,卷积核
filters大小为2
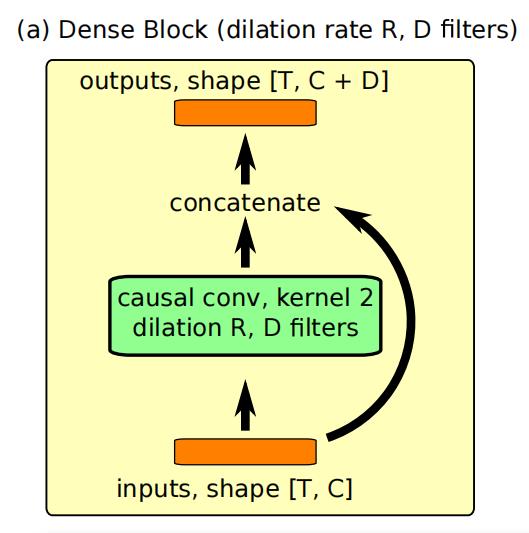
密集块:
一个密集块(DenseBlock)使用膨胀率R和D个卷积核(使用核大小为2)的因果1d卷积,然后将结果与其输入连接起来。使用门控激活函数。门控激活函数请看: 2.4时序卷积网络TCN:因果膨胀卷积、残差连接和跳过连接
class DenseBlock(Layer):
def __init__(self, dilation_rate, filters, kernel_size = 2):
super(DenseBlock, self).__init__()
self.filters = filters
self.dilation_rate = dilation_rate
self.kernel_size = kernel_size
def build(self, input_shape): # Create the weights
self.xf = CasualConv1d(filters = self.filters,
kernel_size = self.kernel_size,
dilation_rate = self.dilation_rate,
)
self.gate = CasualConv1d(filters = self.filters,
kernel_size = self.kernel_size,
dilation_rate = self.dilation_rate,
)
super(DenseBlock, self).build(input_shape)
def call(self, input):
# input is dimensions [batch_shape ,steps, input_dim]
xf = self.xf(input)
xg = self.gate(input)
activations = tf.tanh(xf) * tf.sigmoid(xg) # shape: (batch, steps, filters)
return tf.concat([input, activations], axis = -1)
一个TC块由一系列密集块(DenseBlock)组成,这些块的膨胀率呈指数级增长,直到它们的感受野超过所需的序列长度:
class TCBLOCK(Layer):
def __init__(self, sequence_length, filters):
super(TCBLOCK, self).__init__()
self.filters = filters
self.sequence_length = sequence_length
self.CasualConv_steps = []
for i in range(1, int(tf.math.ceil(tf.math.log(self.sequence_length))) + 1):
self.CasualConv_steps.append(DenseBlock(
filters = self.filters * i,
dilation_rate = 2 ** i -1
))
def call(self, input):
for bock in self.CasualConv_steps:
x = bock(input)
return x
注意力模块
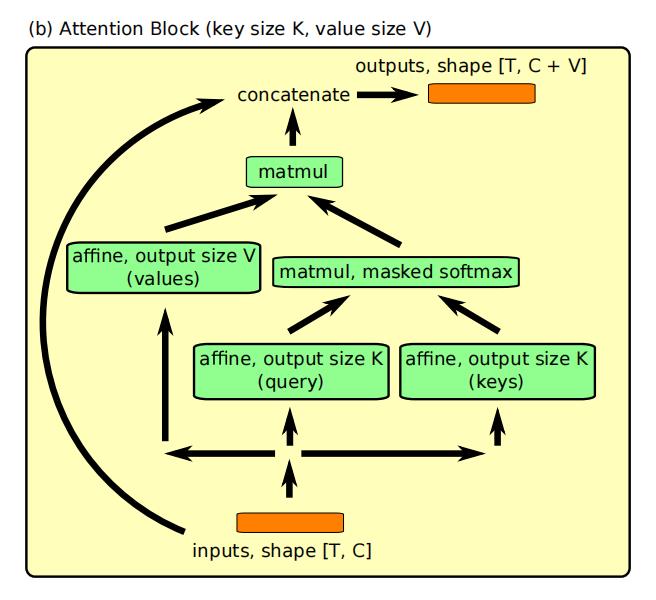
self attention可以让模型在可能的无限大的上下文中精确的定位信息,把上下文信息当做无序的键值对,通过内容对其进行查找.
self attention,使用键值查询的方式对之前的信息进行访问,为了保证在特定的时间节点不能访问未来的键值对,在softmax之前加入了mask,把query与未来的key之间的匹配度设置为负无穷,最后将输出与输入进行拼接。
注
意
块
执
行
(
因
果
的
)
键
值
查
找
,
并
将
输
出
连
接
到
输
入
。
注意块执行(因果的)键值查找,并将输出连接到输入。
注意块执行(因果的)键值查找,并将输出连接到输入。
s
e
l
f
−
a
t
t
e
n
t
i
o
n
计
算
过
程
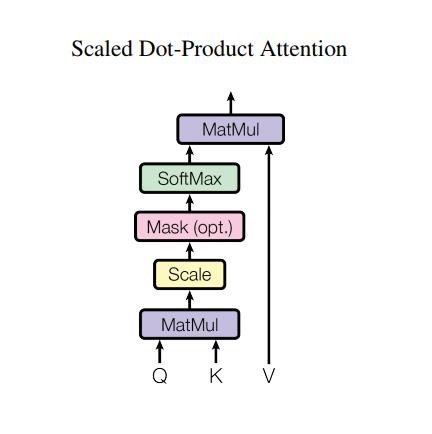
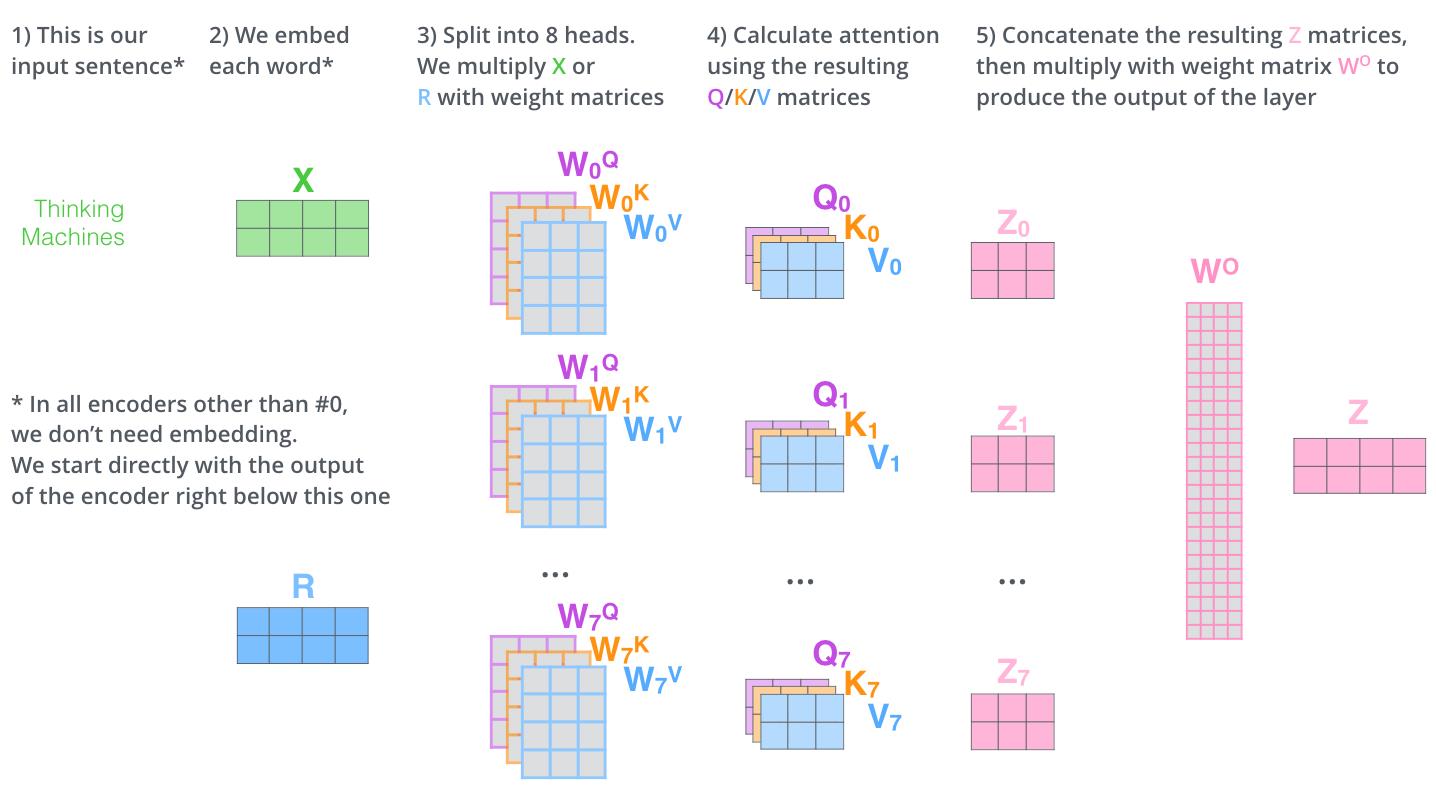
self-attention 计算过程
self−attention计算过程
s
e
l
f
−
a
t
t
e
n
t
i
o
n
:
Q
、
K
、
V
的
训
练
过
程
self-attention:Q、K、V的训练过程
self−attention:Q、K、V的训练过程
self-attention具体内容请看:👉5.3 Transformer意境级讲解
class self_Attention(Layer):
"""
Multi-head attention layer
"""
def __init__(self, hidden_size, num_heads, attention_dropout = 0.):
if hidden_size % num_heads:
raise ValueError("Hidden size ({}) must be divisible by the number of heads ({})."
.format(hidden_size, num_heads))
super(self_Attention,self).__init__()
self.units = hidden_size
self.num_heads = num_heads
self.attention_dropout = attention_dropout
def build(self,input_shape):
super(self_Attention, self).build(input_shape)
self.dense_Q = Dense(self.units, use_bias=False)
self.dense_K = Dense(self.units, use_bias = False)
self.dense_V = Dense(self.units, use_bias = False)
def call(self, input, mask = None):
"""
:param Q: Query: batch * seq_q * Keydim
:param K: Key : batch * seq_v * Key_dim
:param V: Value: batch * seq_v * Value_dim
:param mask: important to avoid the leaks
:return: batch * key_sequence * (units * num_heads)
"""
q = self.dense_q(input) # project the query/key/value to num_heads * units
k = self.dense_k(input)
v = self.dense_v(input)
# multi-heads transfer to
q_ = tf.concat(tf.split(q, self.num_heads, axis = 2), axis = 0) # (batch*heads) * seq_q * Keydim
k_ = tf.concat(tf.split(k, self.num_heads, axis = 2), axis = 0)
v_ = tf.concat(tf.split(v, self.num_heads, axis = 2), axis = 0)
score = tf.matmul(q_, k_, transpose_b = True) # => (batch*heads) * seq_q * seq_v
score /= tf.cast(tf.shape(k_)[-1], tf.float32) ** 0.5
if mask is not None:
score = score * tf.cast(mask, tf.float32)
score = tf.nn.softmax(score)
score = self.dropout(score)
outputs = tf.matmul(score, v_) # (batch*heads) * seq_q * units
outputs = tf.concat(tf.split(outputs, self.num_heads, axis = 0), axis = 2)
outputs = tf.concat([outputs,input ], axis = 2)
return outputs
SNAIL
时序卷积和注意力互相可以互补:前者提供高带宽的方法,代价是受限于 context 的大小,后者可以基于不确定的可能无限大的 context 提供精准的提取。因此,SNAIL 的构建使用二者的组合:使用时序卷积去处理,用注意力机制提取过的内容。
在时序卷积产生的上下文中应用causal attention,可以使网络学习到挑出聚集到的哪些信息,以及如何更好地表示这些信息。SNAIL由两个卷积和attention交错组成。
如
图
:
红
色
的
是
序
列
输
入
,
橘
黄
色
是
时
序
卷
积
层
,
绿
色
是
注
意
力
机
制
。
注
意
力
机
制
中
对
每
个
时
间
步
t
只
对
之
前
的
信
息
进
行
挑
选
,
实
现
时
用
了
M
a
s
k
方
法
。
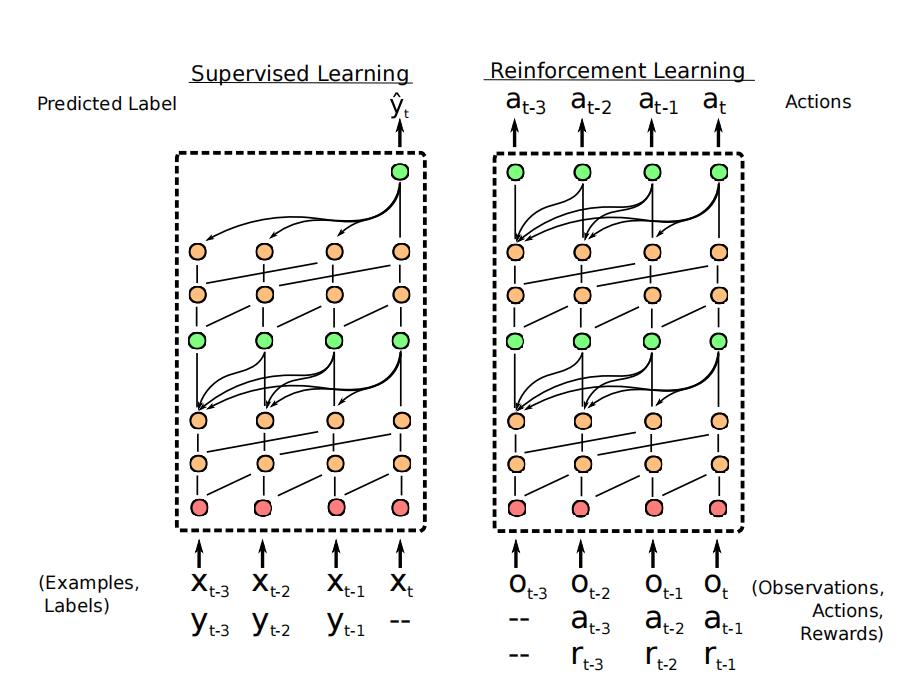
如图:红色的是序列输入,橘黄色是时序卷积层,绿色是注意力机制。\\\\ 注意力机制中对每个时间步 t 只对之前的信息进行挑选,实现时用了Mask方法。
如图:红色的是序列输入,橘黄色是时序卷积层,绿色是注意力机制。注意力机制中对每个时间步t只对之前的信息进行挑选,实现时用了Mask方法。
监督学习设置中,
S
N
A
I
L
\\mathrm{SNAIL}
SNAIL 接收标注样本
(
x
1
,
y
1
)
,
…
,
(
x
t
−
1
,
y
t
−
1
)
\\left(x_{1}, y_{1}\\right), \\ldots,\\left(x_{t-1}, y_{t-1}\\right)
(x1,y1),…,(xt−1,yt−1) 和未标注的
(
x
t
,
−
)
\\left(x_{t},-\\right)
(xt,−) 作 为输入,然后基于标注样本对
y
t
y_{t}
yt 进行预测。
强化学习中输入是 observation-action-reward 三元组序列:
(
o
1
,
−
,
−
)
,
…
,
(
o
t
,
a
t
−
1
,
r
t
−
1
)
\\left(o_{1},-,-\\right), \\ldots,\\left(o_{t}, a_{t-1}, r_{t-1}\\right)
(o 以上是关于8.15 SNAIL:神经注意力元学习的主要内容,如果未能解决你的问题,请参考以下文章