LeetCode:268. 丢失的数字1404. 将二进制表示减到 1 的步骤数

Posted 2021-06-29 南岸青栀*

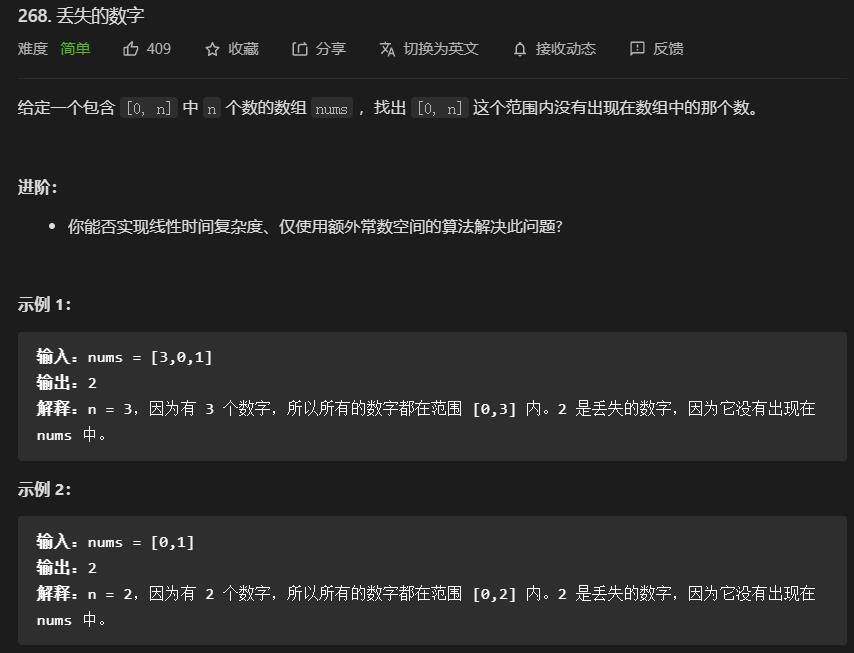
268. 丢失的数字

法1：遍历寻找

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        for i in range(len(nums)+1):
            if i not in nums: return i

法2：哈希表

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        cur = set(nums)
        for i in range(len(nums)+1):
            if i not in cur: return i

法3：数学

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        return len(nums)*(len(nums)+1)//2 - sum(nums)

法4：位运算

由于异或运算（XOR）满足结合律，并且对一个数进行两次完全相同的异或运算会得到原来的数，因此我们可以通过异或运算找到缺失的数字。

算法

我们知道数组中有 n 个数，并且缺失的数在 [0…n][0…n] 中。因此我们可以先得到 [0…n][0…n] 的异或值，再将结果对数组中的每一个数进行一次异或运算。未缺失的数在 [0…n][0…n] 和数组中各出现一次，因此异或后得到 0。而缺失的数字只在 [0…n][0…n] 中出现了一次，在数组中没有出现，因此最终的异或结果即为这个缺失的数字。

在编写代码时，由于 [0…n][0…n] 恰好是这个数组的下标加上 nn，因此可以用一次循环完成所有的异或运算，例如下面这个例子：

下标 0 1 2 3
数字 0 1 3 4
可以将结果的初始值设为 nn，再对数组中的每一个数以及它的下标进行一个异或运算，即：

miss = 4∧(0∧0)∧(1∧1)∧(2∧3)∧(3∧4)
=(4∧4)∧(0∧0)∧(1∧1)∧(3∧3)∧2
=0∧0∧0∧0∧2
=2
​

就得到了缺失的数字为 2。

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        #位运算
        miss = len(nums)
        for i in range(len(nums)):
            miss = miss^i^nums[i]
        return miss

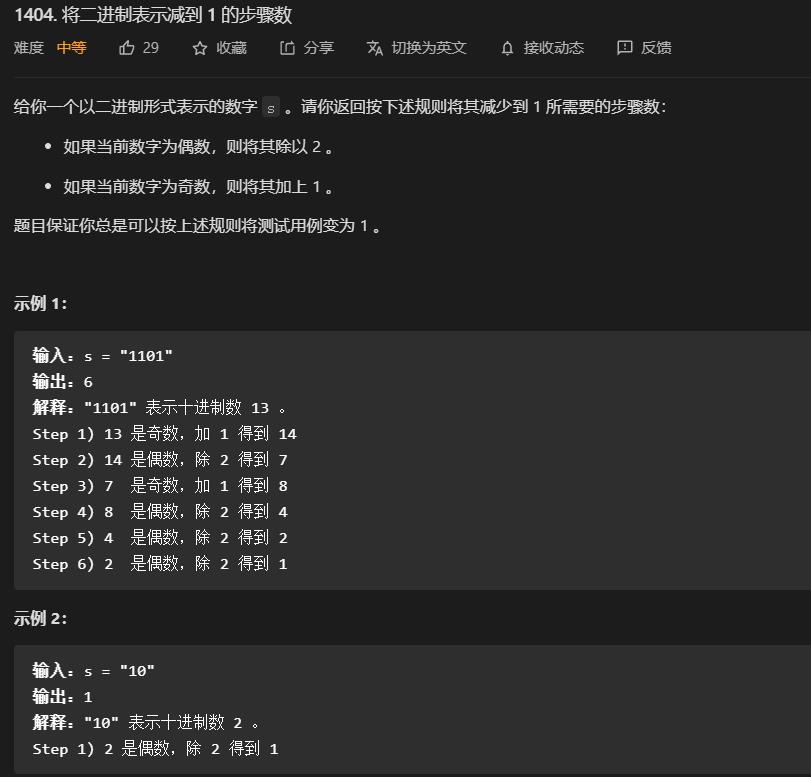
1404. 将二进制表示减到 1 的步骤数

思路1：

class Solution:
    def numSteps(self, s: str) -> int:
        #字符串转为2进制下的十进制
        s = int(s,2)
        cnt = 0
        while s > 1:
            #判断最后一位是否为1，不管结果如何都算一步
            if s&1 == 1:
                s += 1
            elif s&1 == 0:
                s = s>>1
            cnt += 1
        return cnt

思路2：总结归纳

class Solution:
    def numSteps(self, s: str) -> int:
        #特殊情况只是开头有1
        if s[1::].count("0") == len(s)-1: return len(s)-1
        """
        1.一定会进行移位，所以次数为len(s)-1
        2.因为偶数才会直接除，当第一次遇见1时会进行2次操作
        3.在第一个和最后一个1之间的0，会因为进位而进行两次操作，所以统计第一个1和第二个1之间的0的个数 zero
        最后结果 cnt = len(s)-1+2+zero = len(s)+1+zero
        """
        cnt = len(s) + 1
        for i in range(len(s)):
            if "1" not in s[i+1::]: break      
        return cnt + s[:i].count("0")