浮点数式存储：小数在内存中是如何存储的？

Posted 2021-06-29 Debroon

浮点数式存储：小数在内存中是如何存储的？

• • 定点数
  • 浮点数

 

---

小数在内存中是以浮点数的形式存储的。

浮点数是数字（或者说数值）在内存中的一种存储格式，它和定点数是相对的。

浮点数和定点数中的“点”指的就是小数点！

对于整数，可以认为小数点后面都是零，小数部分是否存在并不影响整个数字的值，所以干脆将小数部分省略，只保留整数部分。
 

定点数

所谓定点数，就是指小数点的位置是固定的，不会向前或者向后移动。

假设用4个字节（32位）来存储无符号的定点数，并且约定，前16位表示整数部分，后16位表示小数部分：

如此一来，小数点就永远在第16位之后，整数部分和小数部分一目了然，不管什么时候，整数部分始终占用16位（不足16位前置补0），小数部分也始终占用16位（不足16位后置补0）。

例如，在内存中存储了 10101111 00110001 01011100 11000011，那么对应的小数就是 10101111 00110001 . 01011100 11000011，非常直观。

• 精度：从二进制的角度看，这种定点格式的小数，最多有 32 位有效数字，但是能保证的是 31 位；也就是说，整体的精度为 31~32 位。

  小数部分的最后一位可能是精确数字，也可能是近似数字（由四舍五入、向零舍入等不同方式得到）；除此以外，剩余的31位都是精确数字。

• 小数范围：$2^{16}-2^{-16}$

• 特点：用定点格式来存储小数，优点是精度高，因为所有的位都用来存储有效数字了，缺点是取值范围太小，不能表示很大或者很小的数字。

只是计算机本身就是为了计算大数的，在科学计算中，小数会非常大。

• 例如，电子的质量为：0.0000000000000000000000000009 克 = 9 × 10-28 克

• 例如，太阳的质量为：2000000000000000000000000000000000 克 = 2 × 1033 克

差距有上百个数量级，使用定点数来存储将变得非常困难。

更加科学的方案是按照=后面的指数形式来存储，这样不但节省内存，也非常直观。

这种以指数的形式来存储小数的解决方案就叫做浮点数。浮点数是对定点数的升级和优化，克服了定点数取值范围太小的缺点。

当然，代价就是没有定点数那样精确，浮点数不一定能保存真实的小数，很有可能保存的是一个近似值。

如果类型是浮点数，因为实数在计算和存储时会有误差，因此本来是零的值，由于误差的原因判断为非零。

原因：计算机表示浮点数(float或double类型)都有一个精度限制，对于超出了精度限制的浮点数，计算机会把它们的精度之外的小数部分截断。因此，本来不相等的两个浮点数在计算机中可能就变成相等的了。

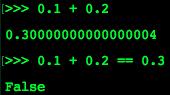
所以，判定方法要改。

‌// 采用绝对精度判断, 原理：判断ta的绝对精度是否小于一个很小的数，如 0.000 001
double eps = 1e-6
if ( fabs(a) <= eps )  // 等于0
if ( fabs(a) - fabs(b) <= eps ) // 俩个数相等
 
// 当变量 a、b 在 eps 精度附近时，会判断失误。还有 【相对精度】 和 【绝对精度+相对精度】 的判断方法

 

浮点数

小数在内存中以科学计数法的形式来存储，具体形式为：

$flt=(-1{)}^{sign}\times mantissa\times bas{e}^{exponent}$

• flt 是要表示的小数。
• sign 用来表示 flt 的正负号，它的取值只能是 0 或 1：取值为 0 表示 flt 是正数，取值为 1 表示 flt 是负数。
• base 是基数，或者说进制，它的取值大于等于 2（例如，2 表示二进制、10 表示十进制、16 表示十六进制……）。数学中常见的科学计数法是基于十进制的，例如 6.93 × 1013；计算机中的科学计数法可以基于其它进制，例如 1.001 × 27 就是基于二进制的，它等价于 1001 0000。
• mantissa 为尾数，或者说精度，是 base 进制的小数，并且 1 ≤ mantissa ＜ base，这意味着，小数点前面只能有一位数字；
• exponent 为指数，是一个整数，可正可负，并且为了直观一般采用十进制表示。

e.g. 19.625从小数转换为浮点数格式

当 base 取值为 2 时，将 19.625 转换成二进制为 10011.101，用浮点形式来表示为：

• 19.625 = 10011.101 = 1.0011101×24

整数部分的二进制形式为：19 = 1×24 + 0×23 + 0×22 + 1×21 + 1×20 = 10011

小数部分的二进制形式为：0.625 = 1×2-1 + 0×2-2 + 1×2-3 = 101

将整数部分和小数部分合并在一起：19.625 = 10011.101

内存中的存储格式：19.625 = 1.0011101×$2^4$

当基数（进制）base 确定以后，指数 exponent 实际上就成了小数点的移动位数：

• exponent 大于零，mantissa 中的小数点右移 exponent 位即可还原小数的值；
• exponent 小于零，mantissa 中的小数点左移 exponent 位即可还原小数的值。

将小数转换成浮点格式后，小数点的位置发生了浮动（移动），并且浮动的位数和方向由 exponent 决定，所以我们将这种表示小数的方式称为浮点数。

此时符号 sign 为 0，尾数 mantissa 为 1.0011101，指数 exponent 为 4。

符号的存储：用 0 表示正数，用 1 表示负数。对于 19.625，这一位的值是 0。

尾数的存储：当采用二进制形式后，尾数部分的取值范围为 1 ≤ mantissa ＜ 2，这意味着：尾数的整数部分一定为 1，是一个恒定的值，这样就无需在内存中提现出来，可以将其直接截掉，只要把小数点后面的二进制数字放入内存中即可。对于 1.0011101，就是把 0011101 放入内存。

如果 base 采用其它进制，比如十进制，整数部分可能是 1~9 之间的任何一个值，这样一来尾数的整数部分就不能省略了，必须在内存中体现出来。

指数的存储：指数是一个整数，并且有正负之分，不但需要存储它的值，还得能区分出正负号来。

为了提高效率，避免繁琐的转换，指数的存储并没有采用补码加符号位的形式，而是自有一套方案。

在六七十年代，计算机界对浮点数的处理比较混乱，各家厂商都有自己的一套规则，缺少统一的业界标准，这给数据交换、计算机协同工作带来了很大不便。

作为处理器行业的老大，Intel 早就意识到了这个问题，并打算一统浮点数的世界。Intel 在研发 8087 浮点数协处理器时，聘请到加州大学伯克利分校的 William Kahan 教授（最优秀的数值分析专家之一）以及他的两个伙伴，来为 8087 协处理器设计浮点数格式，他们的工作完成地如此出色，设计的浮点数格式具有足够的合理性和先进性，被 IEEE 组织采用为浮点数的业界标准，并于 1985 年正式发布，这就是 IEEE 754 标准，它等同于国际标准 ISO/IEC/IEEE 60559。

目前，几乎所有的计算机都支持 IEEE 754 标准，大大改善了科学应用程序的可移植性。

所有，开源是很好的，要是形成了开源的代码行业变成了行业的标准，那就会有声誉。

与定点数相比，浮点数在精度方面损失不小，但是在取值范围方面增大很多。牺牲精度，换来取值范围，这就是浮点数的整体思想。