第三周.02.HAN算法详解
Posted oldmao_2001
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第三周.02.HAN算法详解相关的知识,希望对你有一定的参考价值。
本文内容整理自深度之眼《GNN核心能力培养计划》+
公式输入请参考: 在线Latex公式
泛读HAN
之前的GNN专题里面有涉及到异质图的文章有三篇,分别是:
04metapath2vec
05transE
06GAT
这次要讲的是:Heterogeneous Graph Attention Network
文章发表在The 2019 World Wide Web Conference(CCF A类会议)
是一篇异质图经典的Baseline。
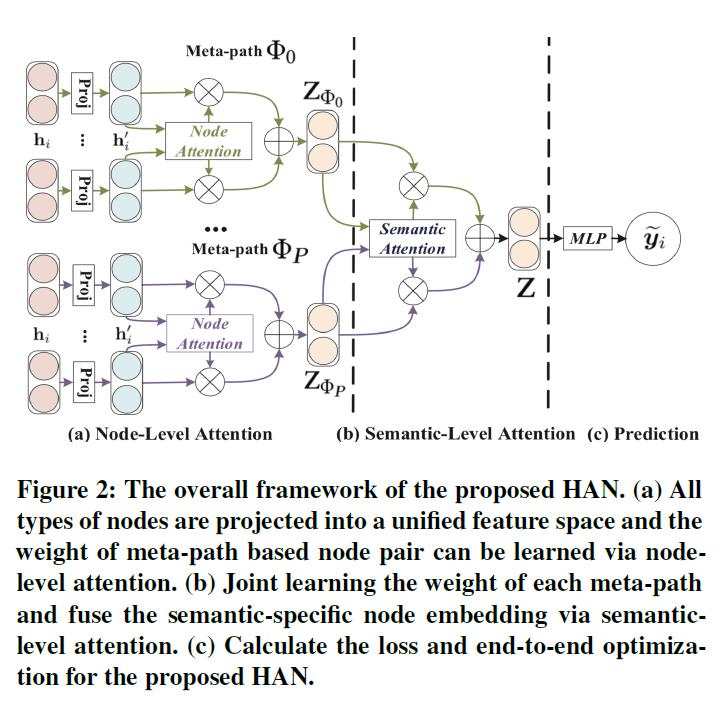
文章中表明,和简单图不一样(节点类型和边类型均只有1种,那么二者之和等于2)该文章研究的图的节点类型和边类型之和要大于2。
∣
A
∣
+
∣
R
∣
>
2
|\\mathcal{A}|+|\\mathcal{R}|>2
∣A∣+∣R∣>2
不同类型的节点,表示他们特征的特征空间是不一样的,甚至维度也都不一样,例如,作者、文章的维度不一样,因此要对不同类型的节点或边,先进行projection:
h
i
′
=
M
Φ
i
⋅
h
i
h_i' = M_{\\Phi_i}\\cdot h_i
hi′=MΦi⋅hi
这样的好处是可以把不同特征空间的向量映射到相同空间上,不然不同维度的向量无法进行加减之类的运算。
这个模型每个metapath都会为节点计算一套特征表示,因此在某个metapath(不同metapath用不同的
ϕ
\\phi
ϕ表示)下的节点间(
h
i
′
,
h
j
′
h_i',h_j'
hi′,hj′)注意力(node-level attention)可以表示为:
e
i
j
Φ
=
a
t
t
n
o
d
e
(
h
i
′
,
h
j
′
;
Φ
)
e_{ij}^\\Phi=att_{node}(h_i',h_j';\\Phi)
eijΦ=attnode(hi′,hj′;Φ)
然后要把上面的注意力用softmax进行归一化(原因之前有说过,每个节点邻居数量不一样,数量少的比数量多的权重算出来要大,因此归一化后才能进行比较)
α
i
j
Φ
=
s
o
f
t
m
a
x
j
(
e
i
j
Φ
)
=
exp
(
σ
(
a
Φ
⋅
[
h
i
′
∣
∣
h
j
′
]
)
)
∑
k
∈
N
i
Φ
exp
(
σ
(
a
Φ
⋅
[
h
i
′
∣
∣
h
j
′
]
)
)
\\begin{aligned}\\alpha_{ij}^\\Phi&=softmax_j(e_{ij}^\\Phi)\\\\ &=\\cfrac{\\exp\\left(\\sigma(a_\\Phi\\cdot[h_i'||h_j'])\\right)}{\\sum_{k\\in \\mathcal{N}_i^\\Phi}\\exp\\left(\\sigma(a_\\Phi\\cdot[h_i'||h_j'])\\right)}\\end{aligned}
αijΦ=softmaxj(eijΦ)=∑k∈NiΦexp(σ(aΦ⋅[hi′∣∣hj′]))exp(σ(aΦ⋅[hi′∣∣hj′]))
其中
σ
\\sigma
σ是激活函数,
h
i
′
∣
∣
h
j
′
h_i'||h_j'
hi′∣∣hj′表示concat,
a
Φ
a_\\Phi
aΦ是metapath
Φ
\\Phi
Φ的节点注意力向量,带T表示转置。
然后节点
i
i
i信息的汇聚表示为:
z
i
Φ
=
σ
(
∑
j
∈
N
i
Φ
α
i
j
Φ
⋅
h
j
′
)
z_i^\\Phi=\\sigma\\left(\\sum_{j\\in \\mathcal{N}_i^\\Phi}\\alpha_{ij}^\\Phi\\cdot h_j'\\right)
ziΦ=σ⎝⎛j∈NiΦ∑αijΦ⋅hj′⎠⎞
文章还把node-level attention进行了扩展,变成multihead attention,就是将node-level attention重复K次,然后把得到的embedding进行拼接。
z
i
Φ
=
∣
∣
1
K
σ
(
∑
j
∈
N
i
Φ
α
i
j
Φ
⋅
h
j
′
)
z_i^\\Phi=||_1^K \\sigma\\left(\\sum_{j\\in \\mathcal{N}_i^\\Phi}\\alpha_{ij}^\\Phi\\cdot h_j'\\right)
ziΦ=∣∣1Kσ⎝⎛j∈NiΦ∑αijΦ⋅hj′⎠⎞
以上是单个metapath
Φ
\\Phi
Φ的节点embedding的计算,针对多个metapath:
{
Φ
1
,
Φ
2
,
⋯
,
Φ
P
}
\\{\\Phi_1,\\Phi_2,\\cdots,\\Phi_P\\}
{Φ1,Φ2,⋯,ΦP},就会得到多个embedding:
{
Z
Φ
1
,
Z
Φ
2
,
⋯
,
Z
Φ
P
}
\\{Z_{\\Phi_1},Z_{\\Phi_2},\\cdots,Z_{\\Phi_P}\\}
{ZΦ1,ZΦ2,⋯,ZΦP}。
对应的图如下所示,每个metapath就是一个圈圈,每个metapath的邻居都不一样:
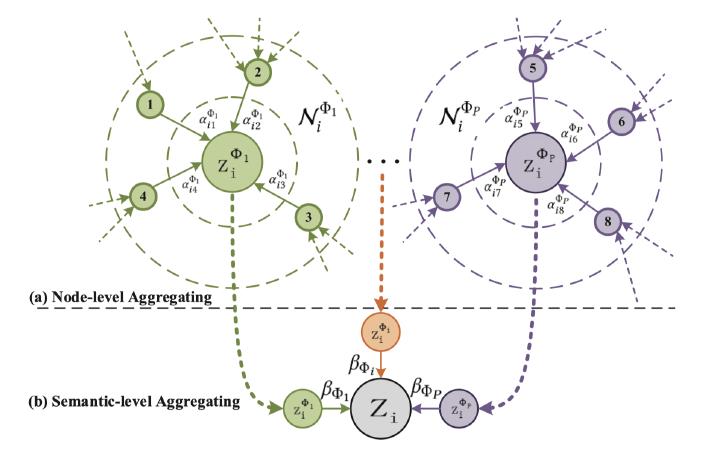
上面根据节点间的注意力在不同的metapath下算出来了
Z
Z
Z,但是:
不同的metapath能不能有attention?在原文的4.2节就提出了:Semantic-level Attention,计算的就是每个metapath对应的embedding的重要程度,因此引入新的注意力权重:
β
\\beta
β,每个metapath都有权重,就可以表示为:
(
β
Φ
1
,
β
Φ
2
,
⋯
,
β
Φ
P
)
(\\beta_{\\Phi_1},\\beta_{\\Phi_2},\\cdots,\\beta_{\\Phi_P})
(β