吴恩达深度学习编程作业（1-1）：Logistic Regression with a Neural Network mindset
Posted 大彤小忆
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了吴恩达深度学习编程作业（1-1）：Logistic Regression with a Neural Network mindset相关的知识，希望对你有一定的参考价值。
本次编程作业对应的完整代码实现(Python版本) → Github链接。
1. 作业简介
本次作业的内容是使用Logistic回归通过训练来判断一副图像是否为猫。
主要内容：如何利用Python的来实现Logistic函数。包括：初始化、计算代价函数和梯度、使用梯度下降算法进行优化等并把他们整合成为一个函数。
2. 工具包
在这个过程中，我们将会用到如下库：
- numpy：Python科学计算中最重要的库；
- h5py：Python与H5文件交互的库；
- mathplotlib：Python画图的库；
- PIL：Python图像相关的库；
- scipy：Python科学计算相关的库。
3. 数据集
3.1 数据说明
对于训练集的标签而言，如果是猫，标记为1，否则标记为0。每一个图像的维度都是(num_px, num_px, 3)，其中，长宽相同，3表示是RGB图像。train_set_x_orig和test_set_x_orig中，包含_orig是由于我们稍候需要对图像进行预处理，预处理后的变量将会命名为train_set_x和train_set_y，train_set_x_orig中的每一个元素对于这一副图像。
3.2 数据预处理
接下来为了方便会对输入数据集的维度进行调整，由原来的(209，64，64，3)调整到 (12288，209)，经过这样的调整之后 ，数据集中的每一列都代表了一张图片，所以这里应该有m_train列 。
为了代表彩色图像，需要RGB3个通道，每个通道的像素值都是0-255。在机器学习中预处理的常见步骤就是数据中心化和标准化，常用的处理方法是对于每个样本都减去均值，然后再除以整个矩阵的标准差。但是在图像中有一种简单的额归一化方法，效果也不错，就是每个样本都除以255（每个通道像素的最大值）。
具体步骤：1）弄清楚要处理的数据集的大小和形状；
2）重塑一些数据集的形状；
3）“标准化”数据。
4. Logistics介绍
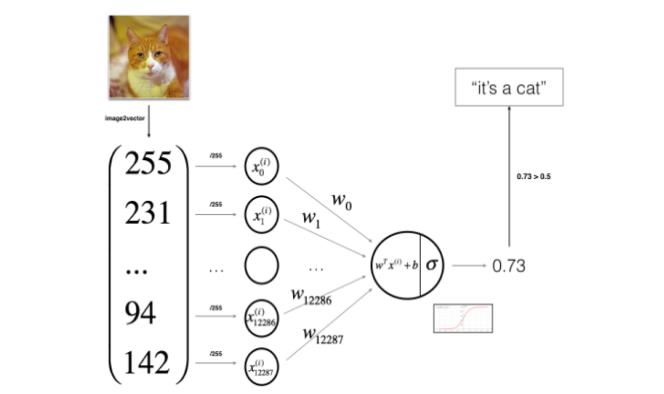
对于每个训练样本x，其误差函数的计算方式如下：
z
(
i
)
=
w
T
x
(
i
)
+
b
z^{(i)}=w^{T}x^{(i)}+b
z(i)=wTx(i)+b
y
^
(
i
)
=
a
(
i
)
=
s
i
g
m
o
i
d
(
z
(
i
)
)
\\hat{y}^{(i)}=a^{(i)}=sigmoid(z^{(i)})
y^(i)=a(i)=sigmoid(z(i))
L
(
a
(
i
)
,
y
(
i
)
)
=
−
y
(
i
)
l
o
g
(
a
(
i
)
)
−
(
1
−
y
(
i
)
)
l
o
g
(
1
−
a
(
i
)
)
L(a^{(i)},y^{(i)})=-y^{(i)}log(a^{(i)})-(1-y^{(i)})log(1-a^{(i)})
L(a(i),y(i))=−y(i)log(a(i))−(1−y(i))log(1−a(i)) 而整体的代价函数计算如下：
J
=
1
m
∑
i
=
1
m
L
(
a
(
i
)
,
y
(
i
)
)
J=\\frac{1}{m}\\sum ^{m}_{i=1}L(a^{(i)},y^{(i)})
J=m1i=1∑mL(a(i),y(i))
5. 创建算法
5.1 算法的创建基本流程
- 定义模型的架构(比如输入特征的数量)
- 初始化模型参数
- 循环
1）计算当前损失（正向传播）
2）计算当前梯度（反向传播）
3）更新参数（梯度下降） - 通常我们会分别实现1-3三个步骤，并且最终放在一个函数model ()中。
5.2 程序实现步骤
- step1：实现sigmod函数
- step2：初始化参数
- step3：前向传播与反向传播
计算公式如下： 得 到 X 计 算 A = σ ( w T X + b ) = ( a ( 0 ) , a ( 1 ) , . . . , a ( m − 1 ) , a ( m ) ) 计 算 代 价 函 数 J = − 1 m ∑ i = 1 m y ( i ) l o g ( a ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a ( i ) ) \\begin{matrix} 得到X\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\\\ 计算A=\\sigma (w^{T}X+b)=(a^{(0)},a^{(1)},...,a^{(m-1)},a^{(m)})\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\\\ 计算代价函数J=-\\frac{1}{m}\\sum ^{m}_{i=1}y^{(i)}log(a^{(i)})+(1-y^{(i)})log(1-a^{(i)}) \\end{matrix} 得到X 吴恩达深度学习：2.1Logistic Regression逻辑回归及其损失函数