信号与系统2021年期末考试命题

Posted 卓晴

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了信号与系统2021年期末考试命题相关的知识，希望对你有一定的参考价值。

简 介： 本文是针对2021年春季学期信号与系统课程期末考试命题所做的准备工作。

关键词： 信号与系统，命题，期末考试

§00 命题说明

1、命题题型

  本次命题是面向2021年本科“信号与系统分析”课程的期末考试题。题目的类型、数量以及分值规划如下：

【表1-1 命题类型以及数量规划】
序列号题目类型题目数量总分值小分值备注
1选择题10101考察基本概念
2判断对错题10101变形的选择题
3填空题10202简化的计算题
4简答题4155对于课堂内容的讨论与延伸
考察基本概念、分析以及应用的能力
判罚标准比较灵活。
5计算题5255变形的作业题
6综合题22010+10综合分析能力；
题目不难，大部分分之是作业送分题

2、各章内容覆盖

【表1-2 各章内容覆盖】
章节题目总分值备注
第一章1-1,1-3,1-4,1-5,2-2,2-96缺少关于信号分解的考察
第二章1-9,2-7,3-5,4缺关于卷积的考察
第三章1-10,2-8,2-10,3-1,3-6,3-8,5-214缺少关于周期信号频谱分析
第四章2-6,3-10,6-111缺少关于信号调制与解调的考察
第五章1-2,2-1,3-2,3-5,3-7,3-9,4-3,5-1,5-3,5-430比较全面
第六章1-6,1-7,1-8,2-4,3-3,3-4,6-220缺少关于全通系统考察
第七章4-1,3-2,5-512比较全面了
第八章2-3,2-5,4-47缺少关于匹配滤波器的考察
  • 建议补充内容：（1）信号的调制与解调；（2）信号的时域卷积以及卷积和运算；（3）匹配滤波器；（4）全通系统

3、辅助信息

（1）DOP 文件

D:\\Teaching\\SignalsSystems\\SS2021S\\Examination\\EXAM-PRE1

（2）网络资源

  下面是就各部分的题目进行准备。实际的试题内容参见最终的考试试卷。后面的各小题顺序与实际试卷中的题目顺序不相同。

 

§01 选择题

  不定项选择题：（10×1=10分，将答案写在试卷前面的答案表格1中）

  1、下面周期信号 f ( t ) f\\left( t \\right) f(t)的频率成分包括（ ）：

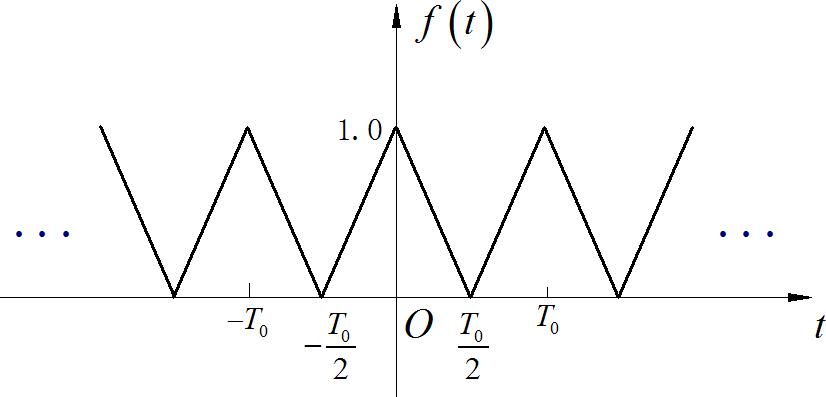
  A. 直流分量； B. 奇次谐波分量； C.偶次谐波分量； D. 只有有限谐波分量

参考答案：A,B

  2、下面给出了拉普拉斯变换定义域s复平面与z变换定义域z复平面上的图形。判断与s平面圆形对应的z平面图形为（ ）：

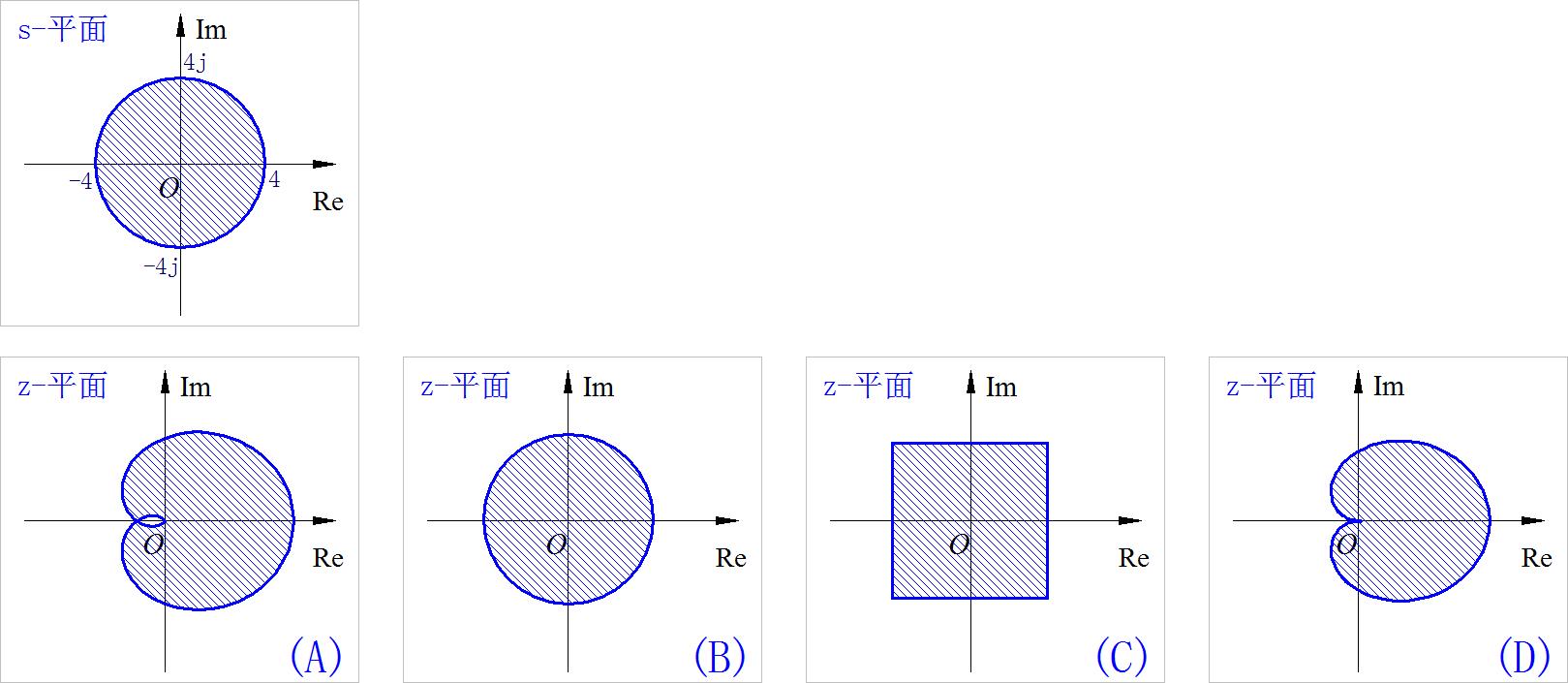
参考答案：A
提示：请注意S域内圆的半径是大于 π \\pi π。这道题来自于学生的提问： s平面上的圆对应的z平面上的图形 。

theta = linspace(0, 2*pi, 200)
r = 3
s = [cos(t)+sin(t)*1j for t in theta]
z = [exp(ss*r) for ss in s]
str = ""
for zz in z:
    str = str + '%f '%(real(zz))
for zz in z:
    str = str + '%f '%(imag(zz))
clipboard.copy(str)
printf(str)

  3、下面信号中，属于功率有限，同时功率不为0的信号包括（ ）：

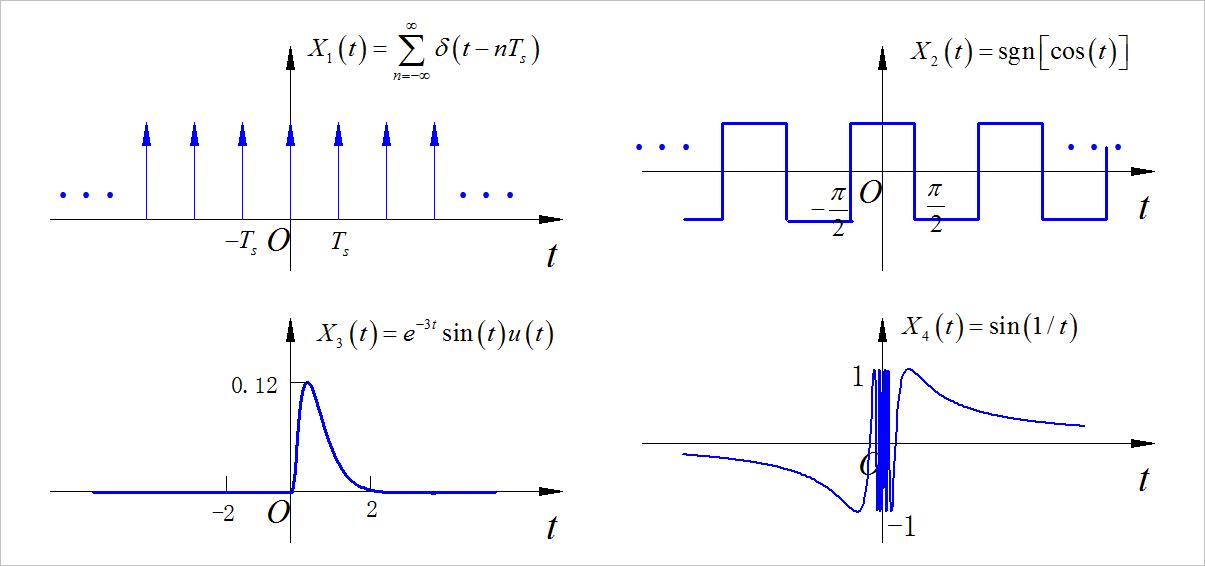
  A. X 1 ( t ) = ∑ n = − ∞ ∞ δ ( t − n T s ) X_1 \\left( t \\right) = \\sum\\limits_{n = - \\infty }^\\infty {\\delta \\left( {t - nT_s } \\right)} X1​(t)=n=−∞∑∞​δ(t−nTs​)

  B. X 2 ( t ) = s g n [ cos ⁡ ( t ) ] X_2 \\left( t \\right) = {\\mathop{\\rm sgn}} \\left[ {\\cos \\left( t \\right)} \\right] X2​(t)=sgn[cos(t)]

  C. X 3 ( t ) = e − 3 t ⋅ sin ⁡ ( t ) ⋅ u ( t ) X_3 \\left( t \\right) = e^{ - 3t} \\cdot \\sin \\left( t \\right) \\cdot u\\left( t \\right) X3​(t)=e−3t⋅sin(t)⋅u(t)

  D. X 4 ( t ) = sin ⁡ ( 1 / t ) X_4 \\left( t \\right) = \\sin \\left( {1/t} \\right) X4​(t)=sin(1/t)

  注：sgn(·) 是符号函数，u(·)是单位阶跃函数；

参考答案：B。 下面是绘制了上面四个信号的波形。从中可以看到只有A,B是周期信号。A的单个周期内的信号为 δ ( t ) \\delta \\left( t \\right) δ(t)，它对应的能量为∞，所以对应的功率为无穷大。因此能够满足条件的信号只有B。


  4、下面信号中属于周期信号的包括有（ ）:

  A. x [ n ] = cos ⁡ [ n 2 ] x\\left[ n \\right] = \\cos \\left[ {n^2 } \\right] x[n]=cos[n2]

  B. x ( t ) = cos ⁡ ( 4.4 π t ) + sin ⁡ ( 0.5 π t ) x\\left( t \\right) = \\cos \\left( {4.4\\pi t} \\right) + \\sin \\left( {0.5\\pi t} \\right) x(t)=cos(4.4πt)+sin(0.5πt)

  C. x [ n ] = sin ⁡ 3 [ 0.15 π ⋅ n ] x\\left[ n \\right] = \\sin ^3 \\left[ {0.15\\pi \\cdot n} \\right] x[n]=sin3[0.15π⋅n]

  D. x ( t ) = e j 0.7 t x\\left( t \\right) = e^{j0.7t} x(t)=ej0.7t

  注：信号自变量为 n 表示离散时间信号；自变量为 t 表示连续时间信号。

参考答案： B， C，D

  5、已知连续时间系统的零状态为 s 0 s_0 s0​，系统的输入信号为 x ( t ) x\\left( t \\right) x(t)。根据下面描述系统输出方程，判断系统为增量线性系统包括（ ）：

  A. y ( t ) = 0.5 s 0 + 4 x ( t ) + s 0 ⋅ x ( t ) + 1 y\\left( t \\right) = 0.5s_0 + 4x\\left( t \\right) + s_0 \\cdot x\\left( t \\right) + 1 y(t)=0.5s0​+4x(t)+s0​⋅x(t)+1

  B. y ( t ) = 5 ⋅ s 0 + x 2 ( t ) y\\left( t \\right) = 5 \\cdot s_0 + x^2 \\left( t \\right) y(t)=5⋅s0​+x2(t)

C. y ( t ) = ∣ s 0 ∣ + 2 ⋅ x ( t ) y\\left( t \\right) = \\left| {s_0 } \\right|{\\rm{ + }}2 \\cdot x\\left( t \\right) y(t)=∣s0​∣+2⋅x(t)

  D. y ( t ) = e − t ⋅ s 0 + 1 π ∫ − ∞ ∞ x ( τ ) t − τ d τ y\\left( t \\right) = e^{ - t} \\cdot s_0 + {1 \\over \\pi }\\int_{ - \\infty }^\\infty {{{x\\left( \\tau \\right)} \\over {t - \\tau }}d\\tau } y(t)=e−t⋅s0​+π1​∫−∞∞​t−τx(τ)​dτ

参考答案：D
注：这个题目在课件上存在。

  6、对于因果系统，下面对于系统描述中属于非最小相位系统的包括（ ）:

  A. 因果离散时间线性时不变系统的零极点分布如下图所示：

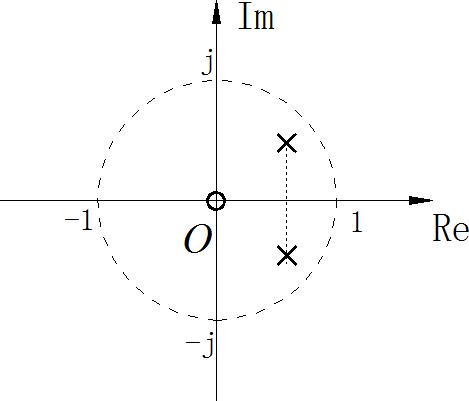
  B.系统的单位阶跃响应曲线为：

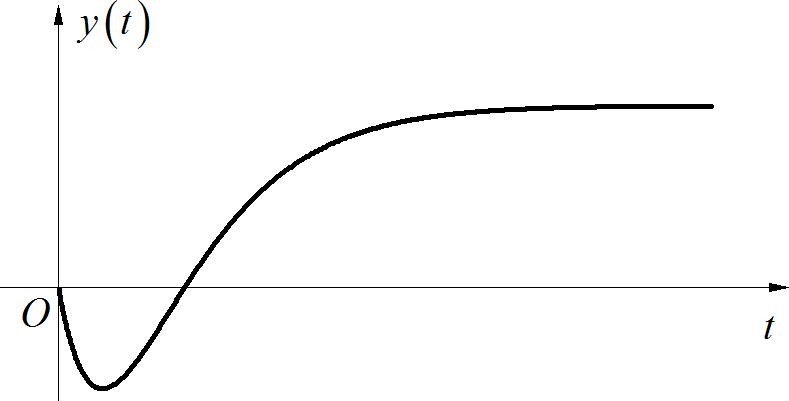
  C. 一阶连续时间线性时不变系统的相频曲线：


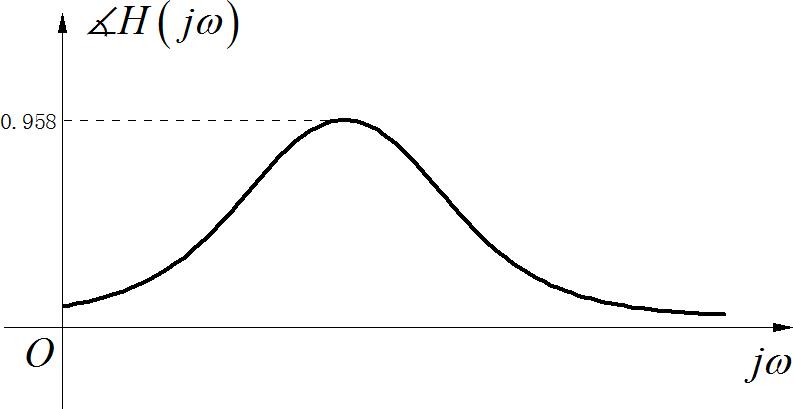
  D. 因果连续时间线性时不变系统的零极点分布如下图所示：

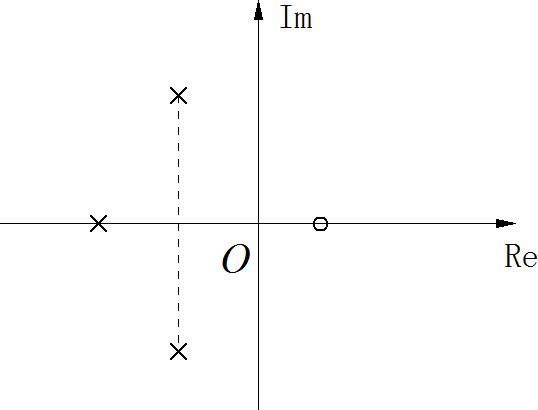
参考答案：B,D

  注：B系统对应的非最小相位系统举例： G ( s ) = − s + 2 ( s + 1 ) 2 G\\left( s \\right) = {{ - s + 2} \\over {\\left( {s + 1} \\right)^2 }} G(s)=(s+1)2−s+2​

from scipy                  import signal
num = [-2, 1]
den = [1, 2, 1]
sys1 = signal.TransferFunction(num, den)
t1, y1 = signal.step(sys1, T = linspace(0, 10, 1000))
clipboard.copy(str(t1)+str(y1))

  C系统对应的相位是最小相位系统举例： G ( s ) = 10 ⋅ s + 1 s + 10 G\\left( s \\right) = 10 \\cdot {{s + 1} \\over {s + 10}} G(s)=10⋅s+10s+1​。

from scipy                  import signal
num = [1, 1]
den = [1, 10]
sys1 = signal.TransferFunction(num, den)
t1, y1 = signal.step(sys1, T = linspace(0, 10, 1000))
def sysPhase山东大学软件学院区块链2018-2019年期末考试试题


 今年期末微积分考试试题：看看你能够在两个小时内做对几道题？


 2021年信号与系统处理期中考试与课堂交互分数


 2021年信号与系统期中考试的补测试题


 信号与系统-2021年春季学期-考试信息


 电子信息研究生3年期间学啥