如何用快排思想在O(n)内查找第K大元素?
Posted 看,未来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何用快排思想在O(n)内查找第K大元素?相关的知识,希望对你有一定的参考价值。

问题实例化
O(n) 时间复杂度内求无序数组中的第 K 大元素。比如,4, 2, 5, 12, 3 这样一组数据,第 3 大元素就是 4。
我的思路
我就不想多说其他的废话了啊,这个呢,其实前几天写STL的时候见过了,不过也是我先想出来了再去看的,和我想的不差。
以快排的思想,我们选择数组区间 A[0…n-1] 的最后一个元素 A[n-1] 作为 pivot,对数组 A[0…n-1] 原地分区,这样数组就分成了三部分,A[0…p-1]、A[p]、A[p+1…n-1]。
如果 p+1=K,那 A[p] 就是要求解的元素;如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1] 区间,我们再按照上面的思路递归地在 A[p+1…n-1] 这个区间内查找。同理,如果 K<p+1,那我们就在 A[0…p-1] 区间查找。
那,都知道快排的时间复杂度为O(nlogn),如果不知道的小伙伴现在可以知道了。那么这个算法的复杂度呢?
我们来看一下最坏的情况,就是一直对半开开到最后,那就是遍历了:
n+n/2+n/4+n/8+……+1 = 2n-1
所以说时间复杂度是多少?
背景:快速排序
推一下快速排序吧,不然看着寒碜了点哈哈哈哈。
快速排序

这些天做题的时候吃了不少 快速排序不熟的亏,我痛下决心,一定要自己写出快速排序的几种实现方法!
什么是快速排序
快速排序是很重要的算法,和傅里叶变化等算法并称二十世纪最伟大的十大算法。
快速排序的核心思维就是“分而治之”,就像封建王朝的“分封制”。将一大块“领土”,依据“嫡庶长幼”,分为不同部分,各个部分在自行细分,直到分无可分之后,便等级森严了。
说白点,就是在序列中找个元素充当中间量,大的往后,小的往前,一分为二,二分为四,四分为八···
那么,快速排序的技术核心,便呼之欲出了。其一就是这个中间量怎么找,其二就是怎么移动各个元素。
基准元素的选择
这个元素的选择啊,并不是说要遵循什么准则,你可以选序列头,序列尾,序列中间元素,都可以。
不过选完之后把基准元素放到序列头的位置。
为了简单,后面我就直接选首元素了。
元素的分配
双边遍历
这个方法呢,如果对快慢指针和双指针不是很了解的朋友可以现在了解一下。

首先啊,确定基准为4,左指针指向第一个元素,右指针指向尾巴。

左指针开始,向前遍历,找到第一个大于基准的元素就停下,轮到右指针,同理。
当两个指针都停下之后,将两个指针所指向的值互换位置。
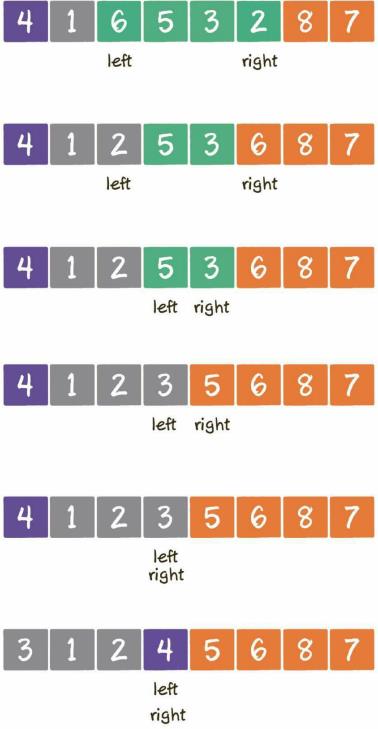
重复上述步骤直到左右指针重合。
重合之后,将基准元素与左右指针当前位置元素进行互换。
一次循环之后,重复上述动作,对划分出的部分再次循环,直到每个部分都只有一个元素为止。
单边遍历
这个是快慢指针实现。

这个mark,是慢指针。快指针没标出来。,依旧找好了基准,快指针从慢指针后一位开始快速遍历,直到遍历到小于基准元素的元素时停滞。

将慢指针前移一位,将当前快慢指针位置元素互换(如果重叠就算了)。然后快指针继续向后走。
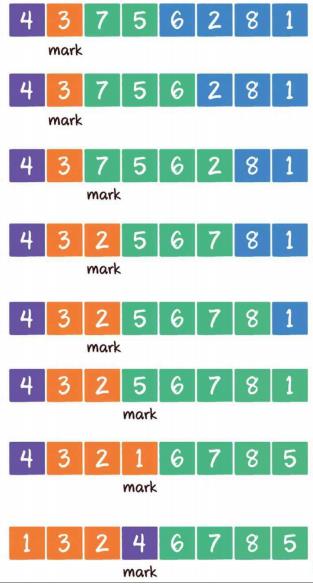
重复上述步骤直到左右指针重合。
重合之后,将基准元素与左右指针当前位置元素进行互换。
一次循环之后,重复上述动作,对划分出的部分再次循环,直到每个部分都只有一个元素为止。
以上是关于如何用快排思想在O(n)内查找第K大元素?的主要内容,如果未能解决你的问题,请参考以下文章