机器学习- 吴恩达Andrew Ng Week6 Regularized Linear Regression and Bias/Variance知识总结

Posted 2021-06-29 架构师易筋

Coursera课程地址

因为Coursera的课程还有考试和论坛，后续的笔记是基于Coursera
https://www.coursera.org/learn/machine-learning/home/welcome

应用机器学习的建议 ML:Advice for Applying Machine Learning

1. 决定下一步尝试什么 Deciding what to try next

预测中的错误可以通过以下方式进行故障排除：

• 获取更多训练示例
• 尝试更小的功能集
• 尝试附加功能
• 尝试多项式特征
• 增加或减少 λ

不要随意选择这些途径之一。我们将在以下部分中探索选择上述解决方案之一的诊断技术。

2. 评估假设 Evaluating a hypothesis

假设对于训练示例可能具有较低的误差，但仍然不准确（因为过度拟合）。

使用给定的训练示例数据集，我们可以将数据分成两组：训练集和测试集。

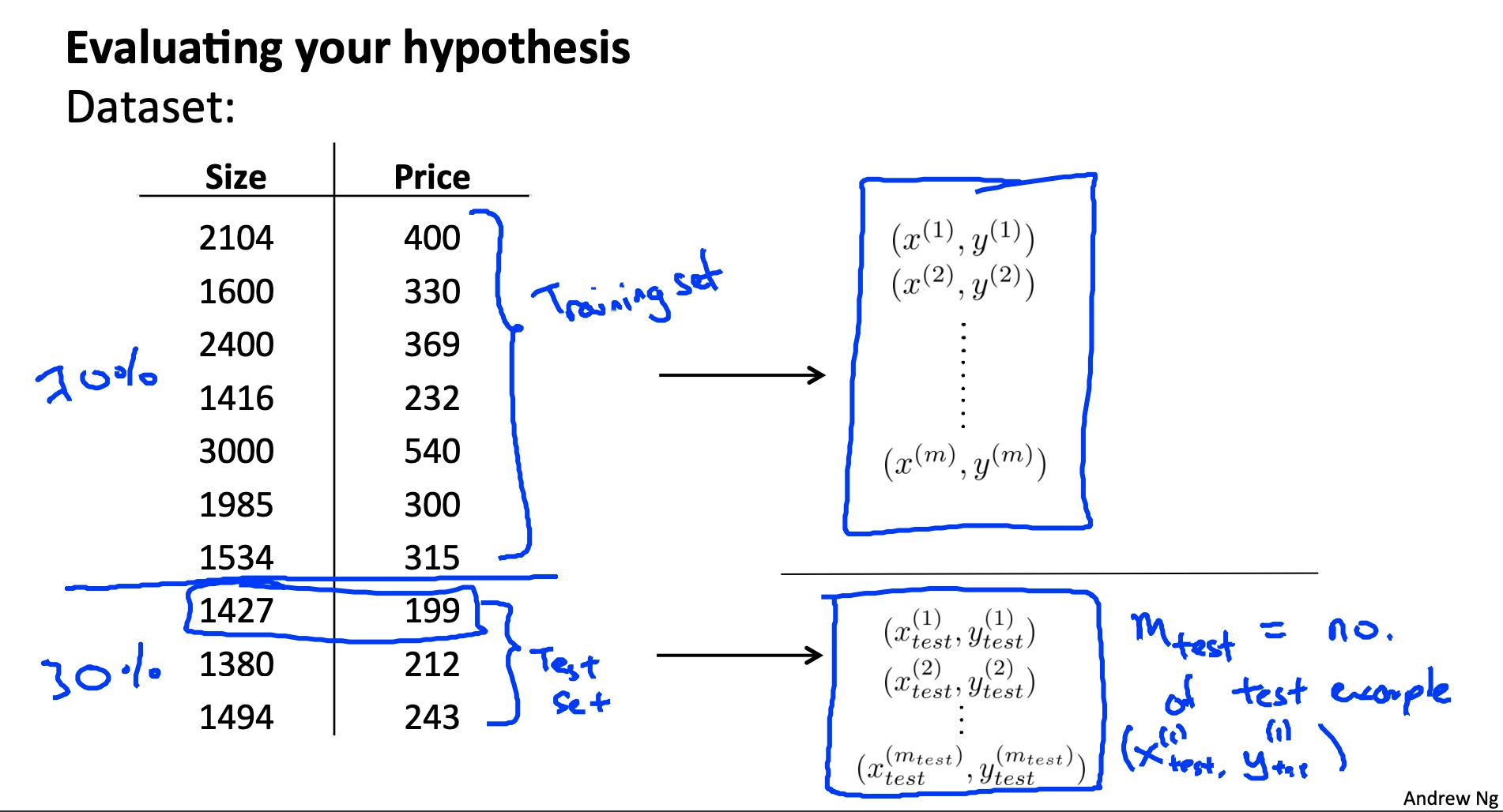
使用这两组的新程序则是：

1. 学 Θ 并最小化 J{train}(Θ) 使用训练集
2. 计算测试集误差 J{test}(Θ)
   

2.1 测试集错误

1. 对于线性回归
   

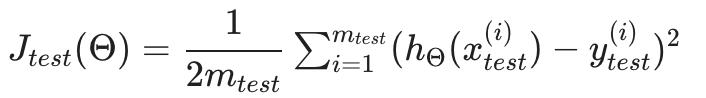
2. 对于分类 ~ 错误分类错误（又名 0/1 错误分类错误）：
   

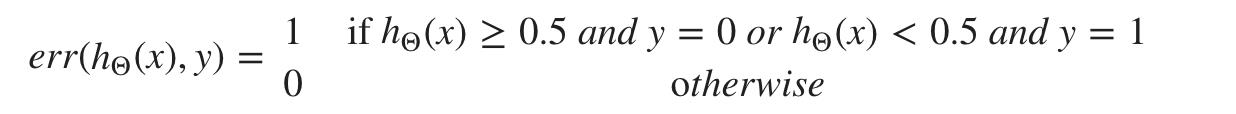
这给了我们一个基于错误分类的二进制 0 或 1 错误结果。

测试集的平均测试误差为

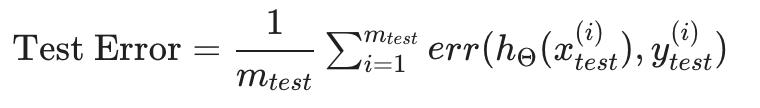
这给了我们错误分类的测试数据的比例。

3. 模型选择和训练/验证/测试集 Model selection and training / validation / test sets

• 仅仅因为学习算法非常适合训练集，并不意味着它是一个好的假设。
• 在训练参数的数据集上测量的假设误差将低于任何其他数据集。

为了选择假设的模型，您可以测试多项式的每个次数并查看错误结果。

3.1 没有验证集（注意：这是一个糟糕的方法 - 不要使用它）

1. 使用每个多项式次数的训练集优化 Θ 中的参数。
2. 使用测试集找出误差最小的多项式次数 d。
3. 还使用测试集估计泛化误差

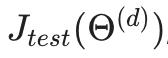
(d = 来自具有较低误差的多项式的 theta)；

在这种情况下，我们使用测试集训练了一个变量 d 或多项式的次数。对于任何其他数据集，这将导致我们的错误值更大。

3.2 交叉验证集的使用

为了解决这个问题，我们可以引入第三个集合，即交叉验证集，作为我们可以用来训练 d 的中间集。然后我们的测试集会给我们一个准确的、非乐观的错误。

将我们的数据集分解为三组的一种示例方法是：

• 训练集：60%
• CV (Cross validation)交叉验证集：20%
• 测试集：20%
  我们现在可以为三个不同的集合计算三个单独的误差值。
  

3.3 使用验证集（注意：此方法假定我们不也使用 CV 集进行正则化）

1. 使用每个多项式次数的训练集优化 Θ 中的参数。
2. 使用交叉验证集找出误差最小的多项式次数 d。
3. 使用测试集估计泛化误差
   
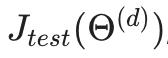
   (d = 来自具有较低误差的多项式的 theta)；
   这样，多项式 d 的次数还没有使用测试集进行训练。

（导师注意：请注意，使用 CV 集来选择 ‘d’ 意味着我们不能将它也用于设置 lambda 值的验证曲线过程）。

4. 诊断偏差与方差 Diagnosing Bias vs. Variance

在本节中，我们检查多项式 d 的次数与我们假设的欠拟合或过拟合之间的关系。

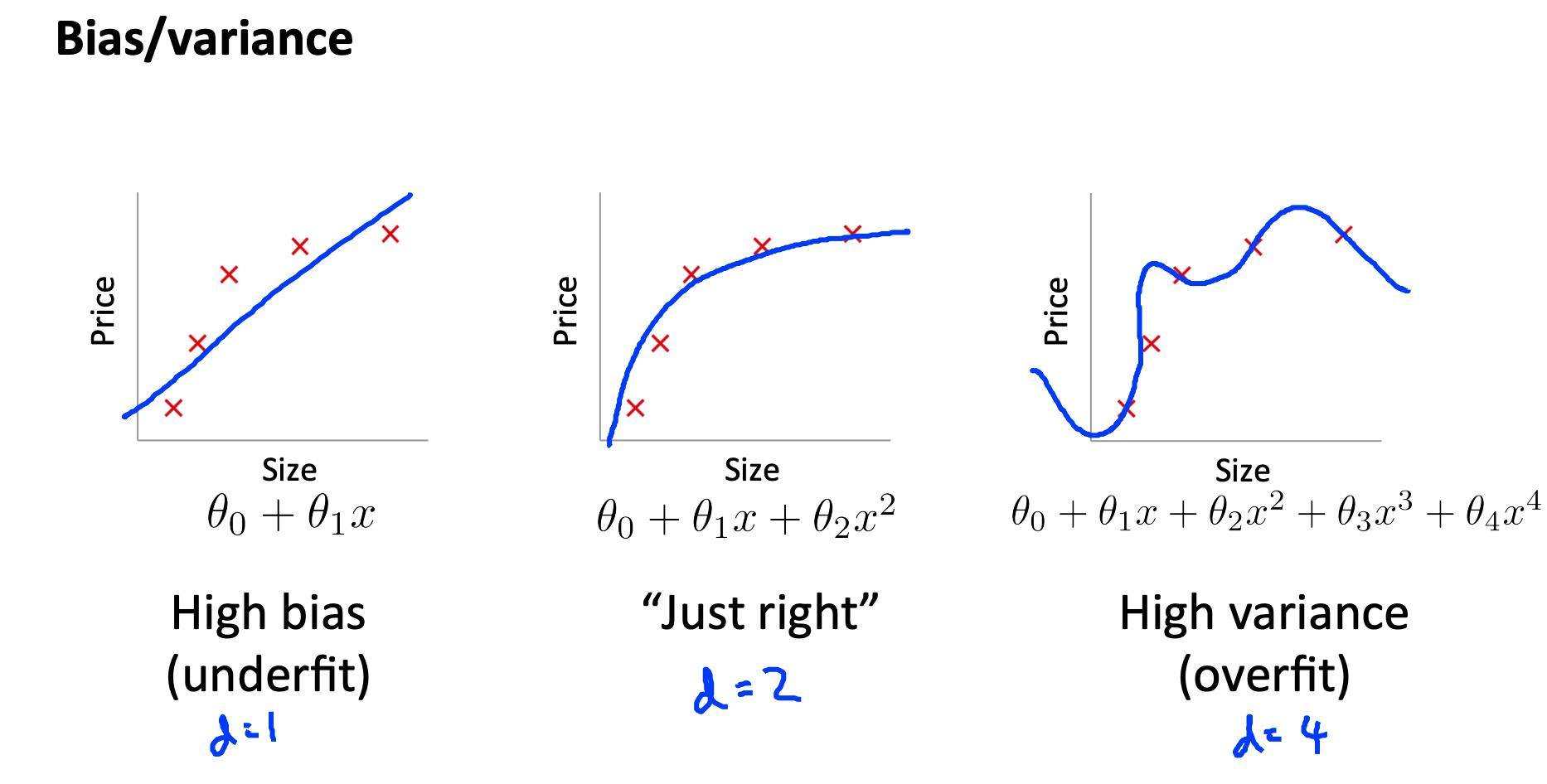
• 我们需要区分偏差Bias或方差Variance是导致错误预测的问题。
• 高偏差Bias是欠拟合，高方差Variance是过拟合。我们需要在这两者之间找到一个中庸之道。
  

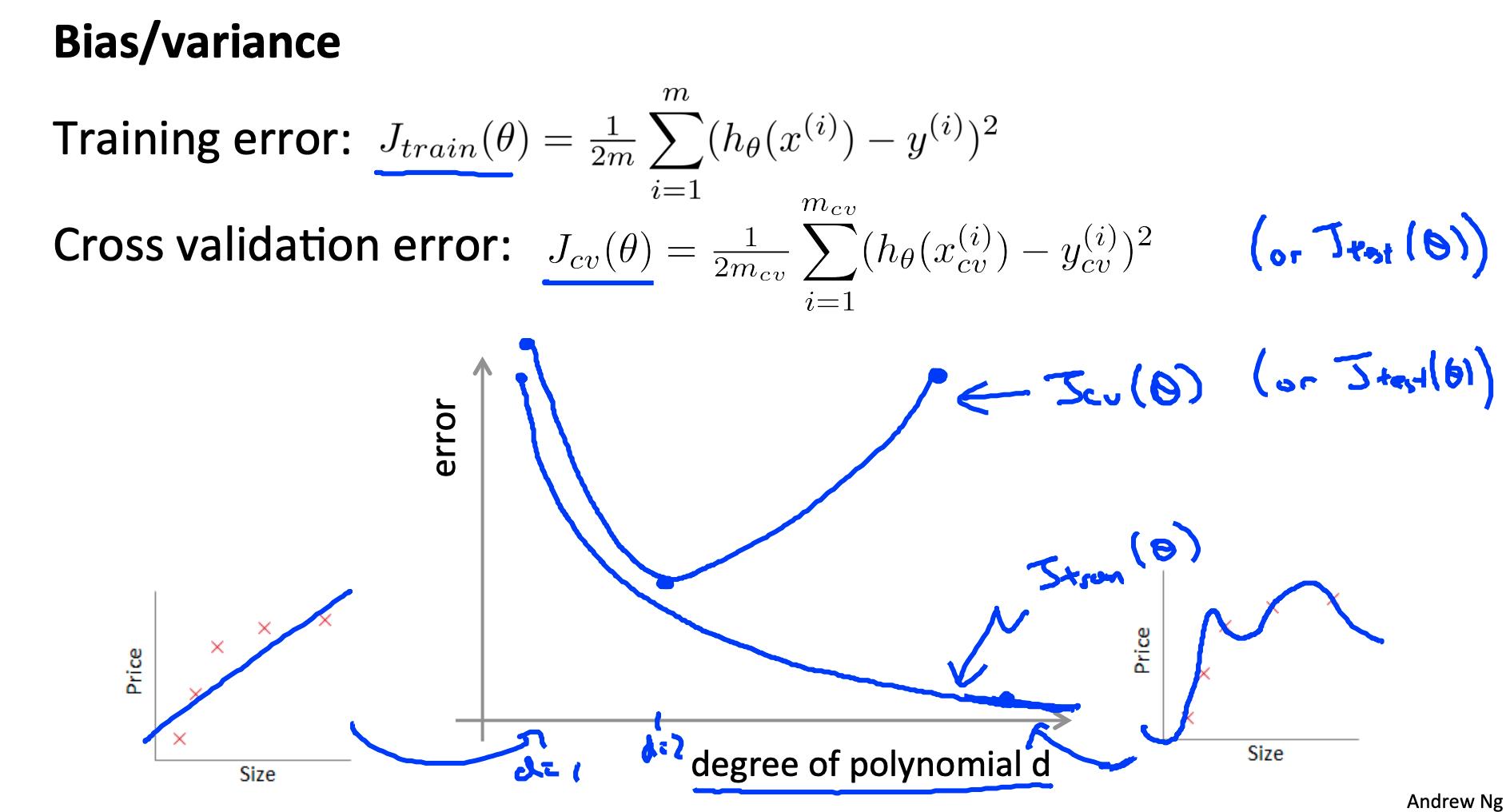
当我们增加多项式的次数 d 时，训练误差将趋于减少。

同时，交叉验证错误将趋向于减少当我们增加ð到一个点，然后它会增加为d的增加，形成的凸曲线。

• 高偏差High bias (underfitting):
  

• 高方差High variance (overfitting):
  
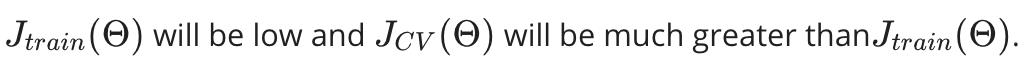
  如下图所示：
  

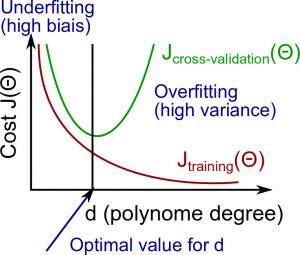
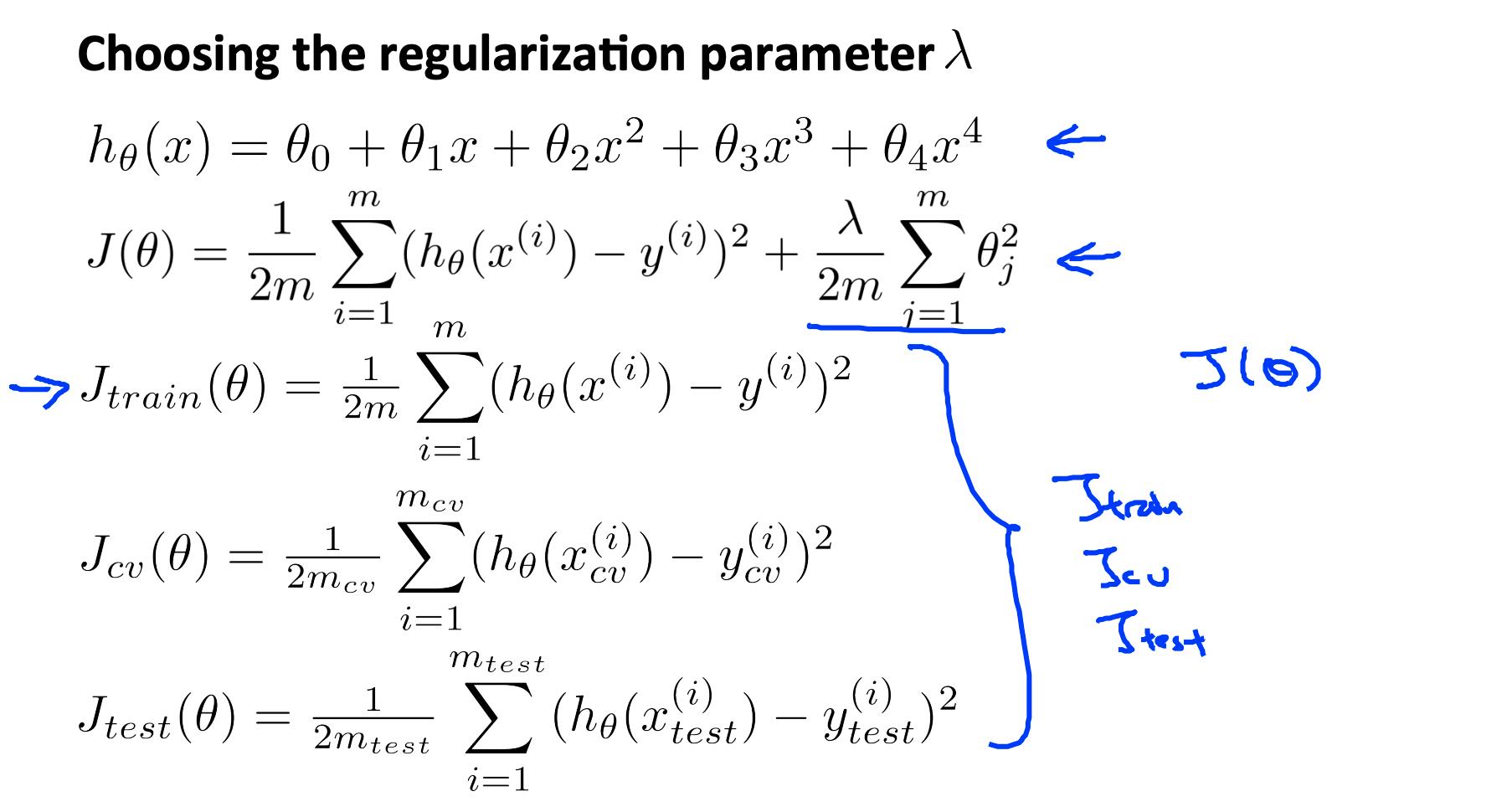
5. 正则化和偏差/方差 Regularization and bias / variance

现在我们将查看正则化参数 λ，而不是查看导致偏差/方差的程度 d。

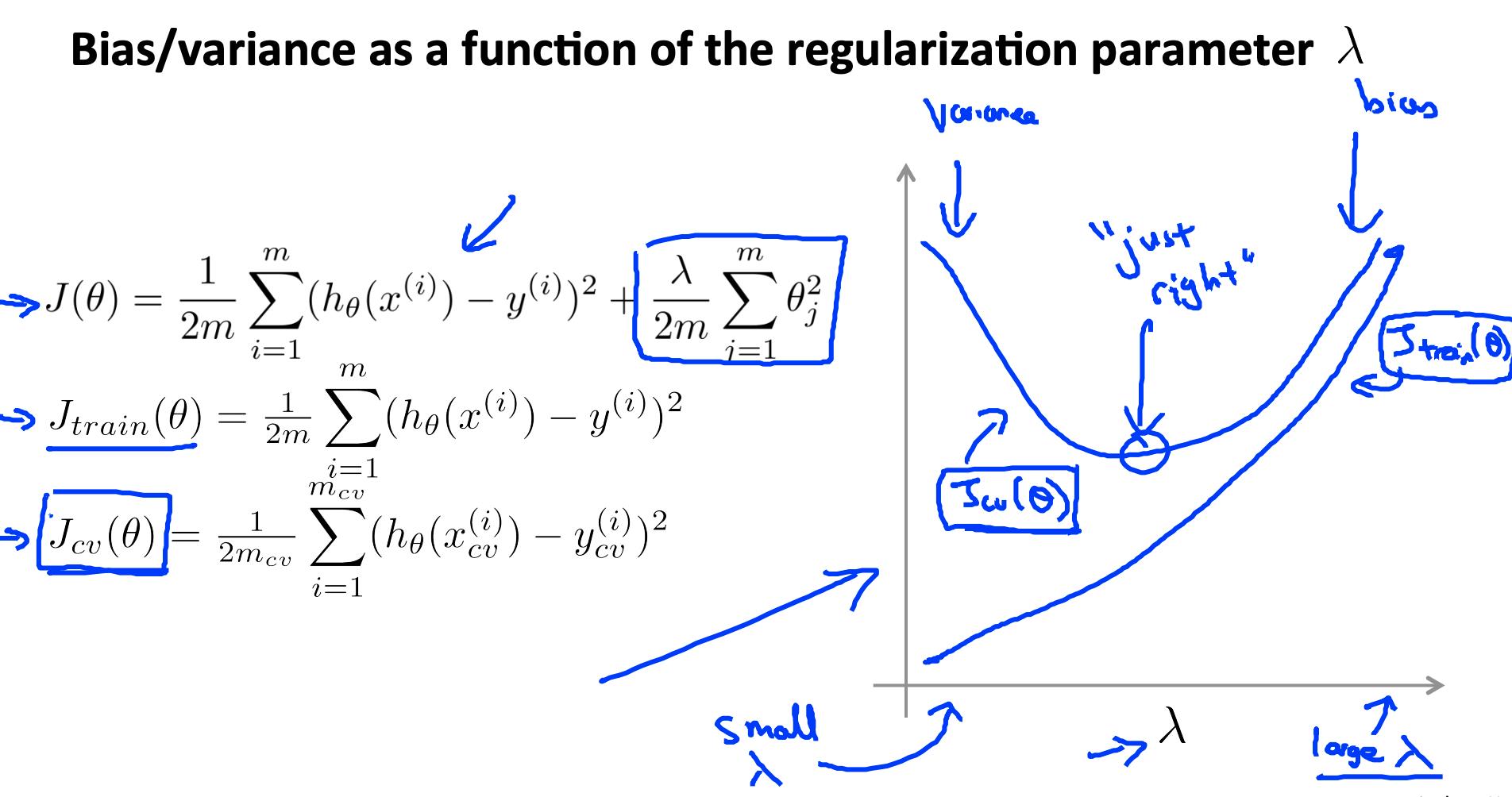
• 大 λ：高偏差（欠拟合）
• 中级λ：恰到好处
• 小λ：高方差（过拟合）
  一个大的 lambda 会严重惩罚所有的 Θ 参数，这大大简化了我们生成的函数的线条，因此会导致欠拟合。

λ与训练集和方差集的关系如下：

• 小 λ :
  

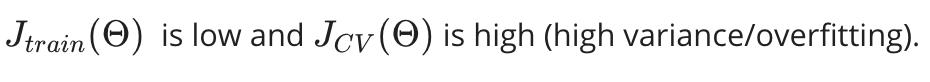
• 中 λ：
  

• 大 λ :
  

下图说明了 lambda 和假设之间的关系：

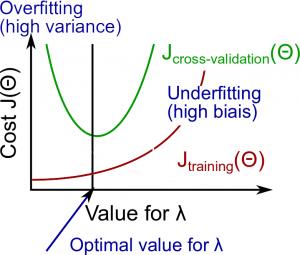
为了选择模型和正则化λ，我们需要：

1. 创建一个 lambda 列表（即 λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24}）；
2. 创建一组不同程度或任何其他变体的模型。
3. 遍历 λs 并且对于每个 λ 浏览所有模型以了解一些 Θ.
4. 使用学习到的 Θ（用 λ 计算）计算交叉验证误差 J_{CV}(θ) 没有正则化或 λ = 0。
5. 选择在交叉验证集上产生最低错误的最佳组合。
6. 使用最佳组合 Θ 和 λ，将其应用于J{test}(θ) 看看它是否对问题有很好的概括。

6. 学习曲线 Learning curves

训练 3 个示例很容易出现 0 个错误，因为我们总能找到一条恰好触及 3 个点的二次曲线。

• 随着训练集变大，二次函数的误差增加。
• 误差值将在某个 m 或训练集大小后趋于稳定。
  

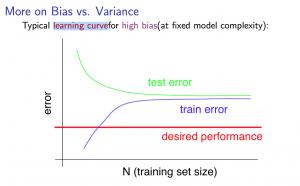
6.1 高偏差 High bias

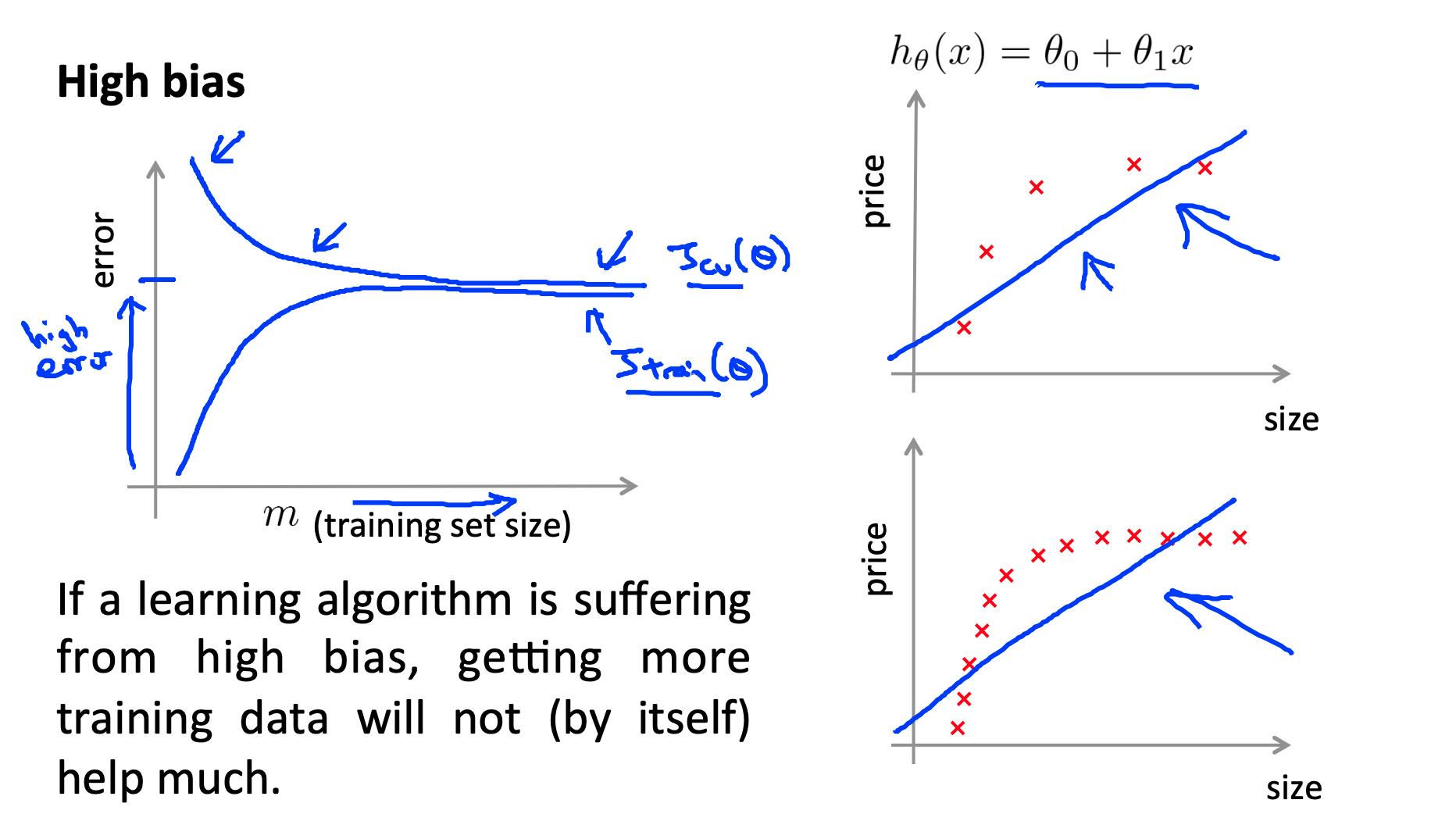
低训练集大小:

大训练集大小:

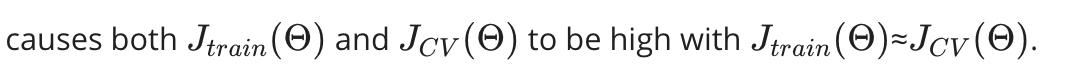
如果学习算法存在高偏差，获得更多的训练数据（就其本身而言）不会有太大帮助。

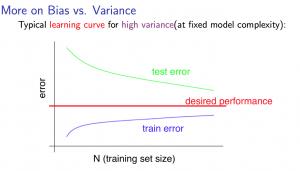
6.2 高方差

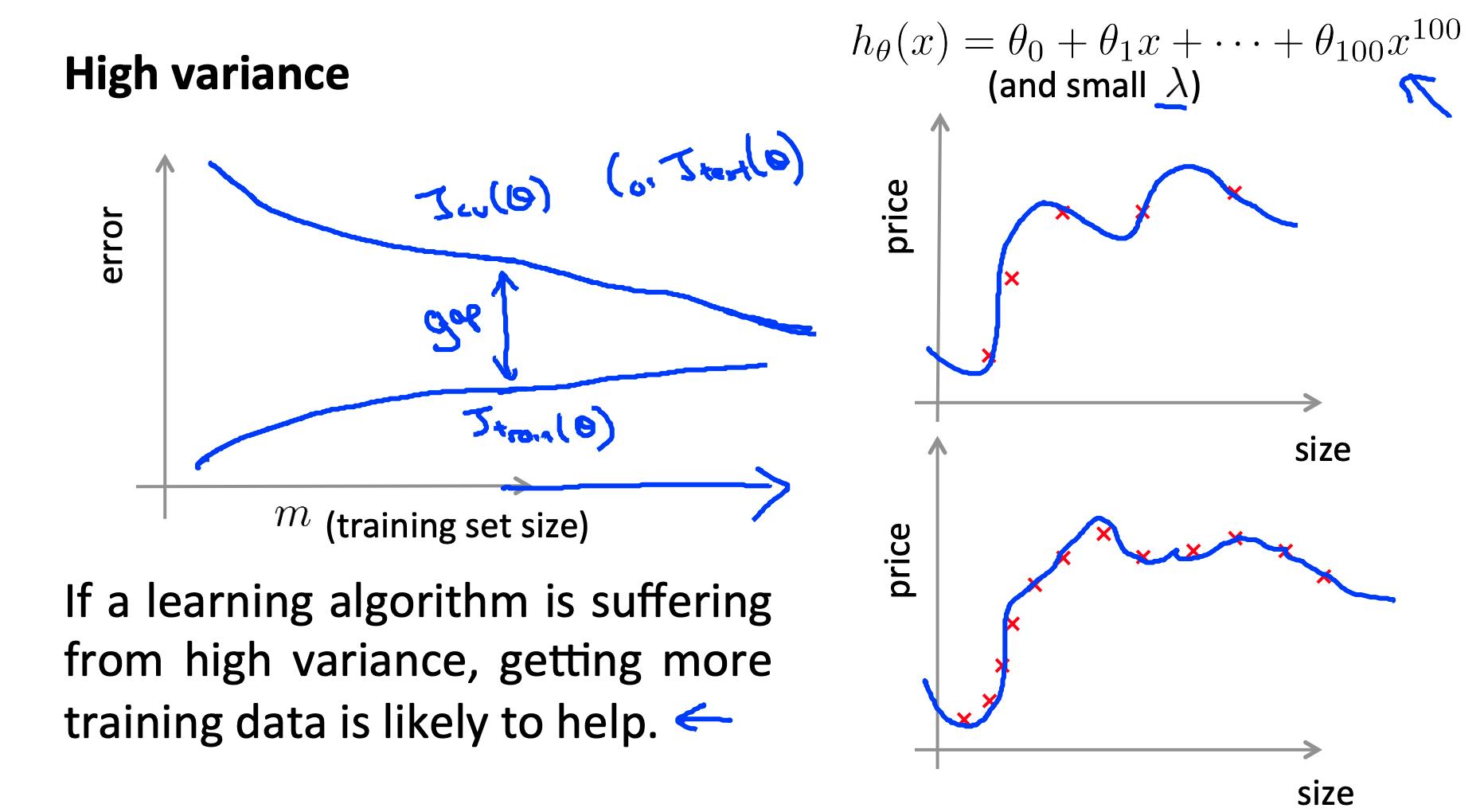
低训练集大小:

大训练集大小:

如果学习算法面临高方差，获得更多的训练数据可能会有所帮助。

7. 决定下一步做什么 Deciding What to do next revisited

我们的决策过程可以分解如下：

• 获取更多训练示例: 修复高方差 high variance
• 尝试更小的功能集: 修复高方差 high variance
• 添加功能: 修复高偏差 high bias
• 添加多项式特征 * 修复高偏差 high bias
• 减小λ: 修复高偏差 high bias
• 增加λ: 修复高方差 hign variance

7.1 诊断神经网络 Diagnosing Neural Networks

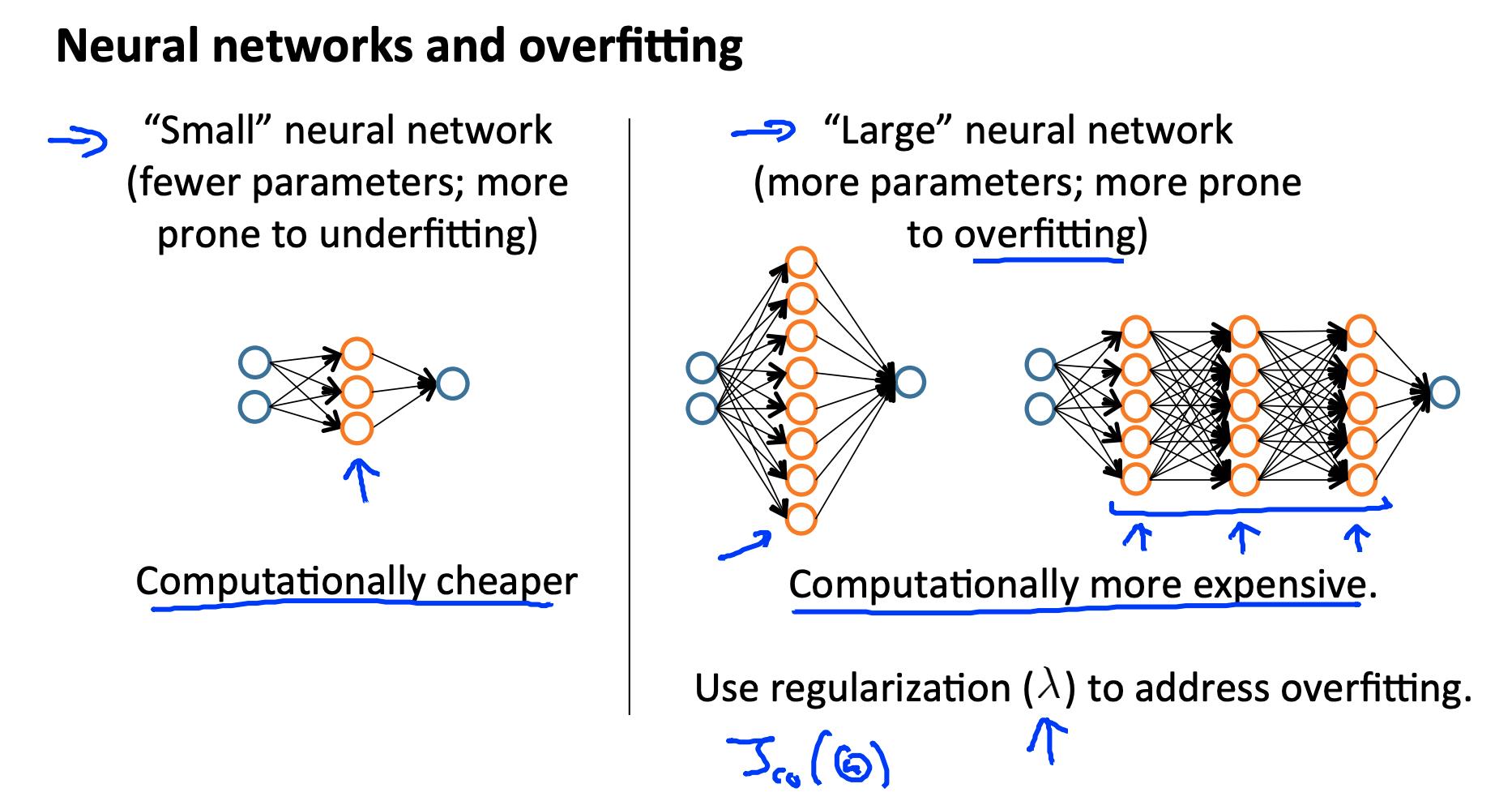
• 参数较少的神经网络容易出现欠拟合。它在计算上也更便宜。
• 参数较多的大型神经网络容易过拟合。它在计算上也是昂贵的。在这种情况下，您可以使用正则化（增加 λ）来解决过拟合问题。

使用单个隐藏层是一个很好的初始默认设置。您可以使用交叉验证集在多个隐藏层上训练神经网络。

7.2 模型选择 Model Selection：

选择多项式的阶数 M。

我们如何知道哪些参数 Θ 留在模型中（称为“模型选择”）？

有几种方法可以解决这个问题：

• 获取更多数据（非常困难）。
• 选择最适合数据而不过度拟合的模型（非常困难）。
• 通过正则化减少过拟合的机会。

7.2.1 偏差Bias：近似误差（期望值和最优值之间的差异）

• 高偏差 = 欠拟合 UnderFitting (BU)
  

7.2.2 方差Variance：由于有限数据造成的估计误差

• 高方差 = 过拟合 OverFitting (VO)
  

7.2.3 偏差Bias-方差Variance权衡的直觉：

• 复杂模型 => 对数据敏感 => 受 X 变化影响很大 => 高方差 hign variance，低偏差 low bias。
• 简单模型 => 更严格 => 不会随着 X 的变化而改变 => 低方差 low variance，高偏差 hign bias。

学习中最重要的目标之一：找到一个在偏差-方差权衡中恰到好处的模型。

7.2.4 正则化效果 Regularization Effects：

• λ 的小值允许模型对噪声进行微调，从而导致大方差 large variance => 过拟合 overfitting。
• λ 拉重参数的大值为零导致大偏差 large bias => 欠拟合 under-fitting。

7.2.5 模型复杂性影响 Model Complexity Effects：

• 低阶多项式（低模型复杂度）具有高偏差hign bias和低方差low variance。在这种情况下，模型的一致性很差。
• 高阶多项式（高模型复杂度）非常适合训练数据，而测试数据非常差。这些对训练数据的偏差low bias很小，但方差high variance很高。
• 实际上，我们希望在两者之间选择一个模型，它可以很好地概括，但也可以很好地拟合数据。

7.3 运行诊断时的典型经验法则是：

• 更多的训练示例修复了高方差hign variance但不修复高偏差hign bias。
• 较少的特征可以修复高方差hign variance但不能修复高偏差hign bias。
• 附加功能修复了高偏差high bias但不修复高方差high variance。
• 多项式和交互功能的添加修复了高偏差hign bias但不修复高方差hign variance。
• 使用梯度下降时，减少 lambda 可以解决高偏差high bias，增加 lambda 可以解决高方差high variance（lambda 是正则化参数）。
• 使用神经网络时，小神经网络更容易欠拟合under-fitting，大神经网络容易过拟合over-fitting。网络规模的交叉验证是一种选择替代方案的方法。

参考

https://www.coursera.org/learn/machine-learning/resources/LIZza

https://www.coursera.org/learn/machine-learning/supplement/7BHrF/lecture-slides