链表有环的一些常见问题，看这就够了

Posted 2021-06-29 两片空白

文章目录

• 1.如何判读链表有环
• • 引申问题
  • • 问题1
    • 问题2
    • 问题3

1.如何判读链表有环

链表存在有环的逻辑结构可以这样理解：

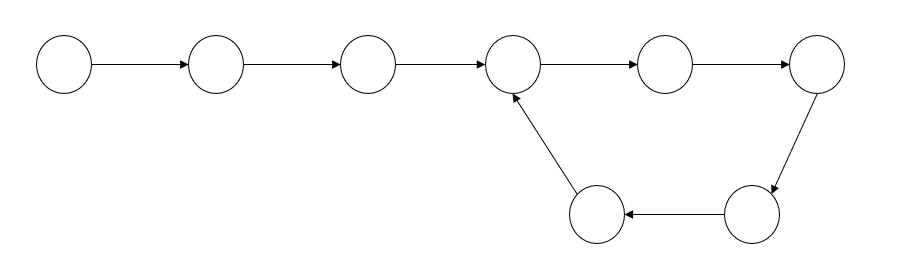
但是实际链表并不存在这些箭头，物理结构为链表结构信息的指针域里存放的是下一个结点的地址。带环就是最后一个结点的地址存的并不是NULL了，
而是链表中的一个结点的地址。

如何证明一个链表是否有环呢？

最好的方法是使用快慢指针法。
快慢指针法就是定义两个指针slow和fast，一开始两指针指向链表头。slow指针每次只前进一个结点，fast指针每次前进两个结点。如果链表有环，两指针就会相遇(两指针相等，也就是地址相等)，没有环的话，快指针就会走向空。

代码如下：

bool hasCycle(struct ListNode *head) {
    if(head==NULL){
        return false;
    }
    struct ListNode *slow=head;//定义快慢指针
    struct ListNode *fast=head;
    while(slow->next&&fast->next){//防止越界
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast){//相等说明有环
            return true;
        }
    }
    return false;

}

引申问题

相信你们可能会有些疑惑，为什么慢指针走一步，快指针，走两步呢，他们一定会相遇吗？可不可以快指针走3步，4步，x步呢？思考一下。

问题1

1.为什么慢指针走一步，快指针走两步，一定会在环里相遇，会不会永远不相遇呢？
答案是：一定会相遇。

当快慢指针都进环了，假设快慢指针间的距离为N，当快慢指针走一步，他们之间的距离就缩短了1，再走一步就缩短了2…最后肯定他们之间的距离会缩短到0。

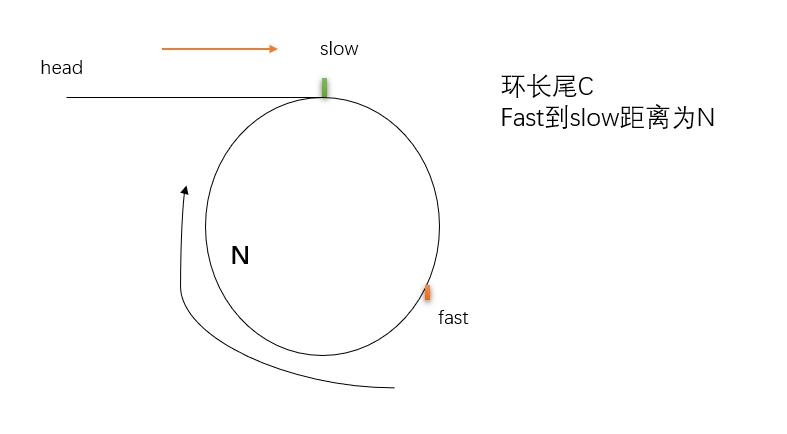
问题2

2.慢指针走1步，快指针走3步，4步，走n步行不行？
答案是：不行。

假设快指针走3步，慢指针走1步。当快慢指针都进环后，假设快慢指针间的距离为N，当快慢指针走一步，他们之间的距离就缩短了2，再走一步，快慢指针之间交开始的距离缩短了4，如图：

当一开始慢指针进环时，fast与slow的距离 如果是奇数时，fast指针正好会错过slow指针，并且正好在他前面一个。然后就会在环里转圈，假设环的长度为C，fast与slow间的距离就是C-1，当C为偶数时，C-1就是奇数，就上面结论，fast指针将会错过slow并且永远不会遇上。

总结：当快指针走三步，慢指针走一步时。当慢指针走入环时，快指针与慢指针的距离为奇数，环的长度为偶数时，永远遇不上。这样其它步长情况也可能会出现遇不上的情况。

问题3

3.求入环结点

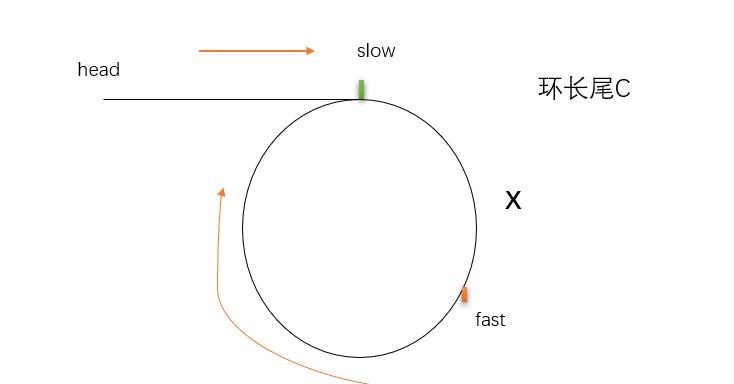
假设快指针走两步，慢指针走一步。头节点到入环结点距离为L，环入口结点 到快慢指针相遇结点距离为X，环的长度为C。
当快慢指针相遇，快慢指针走的距离：
慢指针：L+X
快指针：L+N*C+X(N为快指针围着环走的圈数)
为什么有个N，假设环C很小，L很长，快指针可能在里面转了很多圈了。
然后就会有：2*(L+X)=L+N*C+X(2倍慢指针走的距离就是快指针走的距离，因为快指针走的步数时慢指针的两倍)
所以就有：
L+X=N*C —> L=N*C-X
所以求环链表入环结点思路有：当快慢指针相遇时，让一个指针指向链表头，然后一起一个节点一个结点走，一定会在入口结点相遇。

struct ListNode *detectCycle(struct ListNode *head) {
    if(!head){
        return NULL;
    }
    struct ListNode *slow=head;
    struct ListNode *fast=head;
    while(slow&&fast&&fast->next){
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast){//有环
            struct ListNode *cur=head;//让一个指针指向链表头
            while(cur!=fast){//一起往后走
                cur=cur->next;
                fast=fast->next;
            }
            return cur;//相遇在环入口结点
        }

    }
    return NULL;
    
}