面试高频算法难题：数组中的第K个最大元素

Posted 2021-06-29 java构架师

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了面试高频算法难题：数组中的第K个最大元素相关的知识，希望对你有一定的参考价值。

目是什么意思呢？比如给定的无序数组如下：

如果 k=6，也就是要寻找数组中的第6大元素，这个元素是哪一个呢？

显然，数组中第一大的元素是24，第二大的元素是20，第三大的元素是17 …第6大的元素是9。

让我想想啊……

对了，我可以先把无序数组排序，然后数出排序后的第k个元素！

方法1：排序法

这是最容易想到的方法，先把无序数组从大到小进行排序，排序后的第k个元素，自然就是数组中的第k大元素。

先进行排序的话，算法时间复杂度是O（nlogn），

性能有些差，有没有更优化的方法？

让我想想啊……

对了，我可以维护一个长度为k的数组，有序存储当前k个较大的元素！

方法2：插入法

维护一个长度为k的有序数组A，用于存储已知的k个较大的元素。

接下来遍历原数组，每遍历到一个元素，和数组A中最小的元素相比较，如果小于等于数组A的最小元素，继续遍历；如果大于数组A的最小元素，则插入到数组A中，并把曾经的最小元素“挤出去”。

比如k=3，先把最左侧的7,5,15三个数有序放入数组A当中，代表当前最大的3个数。

这时候，遍历到元素3，由于3<5，继续遍历。

接下来遍历到17，由于17>5，插入到数组A的合适位置，类似于插入排序，并把原先最小的元素5“挤出去”。

继续遍历原数组，一直遍历到数组的最后一个元素…

最终，数组A中存储的元素是24,20,17，代表着整个数组中最大的3个元素。此时数组A中最小的元素17，就是我们要寻找的第k大元素。

这个方法的时间复杂度是O（nk），如果k的值比较大，其性能可能还不如方法一。

还有没有更优化的方案？

好像没有更快的方法了吧……

呵呵，没关系，回家等通知去吧！

解题思路

小灰，你刚刚去面试了？结果怎么样？

唉……

大黄，要想找到无序数组中的第k大元素，有什么性能较高的方法吗？

这是一道很经典的算法题，解法有很多种，

其中最容易想到的是利用二叉堆来解决。

关于二叉堆的概念，在上一本《漫画算法》中我们介绍过。简而言之，二叉堆是一种特殊的完全二叉树，它包含最大堆和最小堆两种形式。

其中最小堆的特点，是每一个父结点都小于等于自己的子结点，堆顶是整个堆中最小的结点。要解决这个算法题，我们可以利用最小堆的特性。

可是，最小堆和这个算法题究竟有什么关系呢？

别急，让我来解释一下这个方法的思路。

方法3：最小堆法

维护一个容量为k的最小堆，堆中的k个结点代表着数组当前最大的k个元素，而堆顶显然是这k个元素中的最小值。

遍历原数组，每遍历一个元素，就和堆顶比较，如果当前元素小于等于堆顶，说明该元素一定不是最大的k个元素之一，继续遍历；如果元素大于堆顶，说明该元素有可能是最大的k个元素之一，把当前元素放在堆顶位置，并调整二叉堆（下沉操作）。

遍历结束后，堆顶就是数组的最大k个元素中的最小值，也就是第k大元素。

假设k=5，具体的执行步骤如下：

1. 把数组的前k个元素构建成堆。

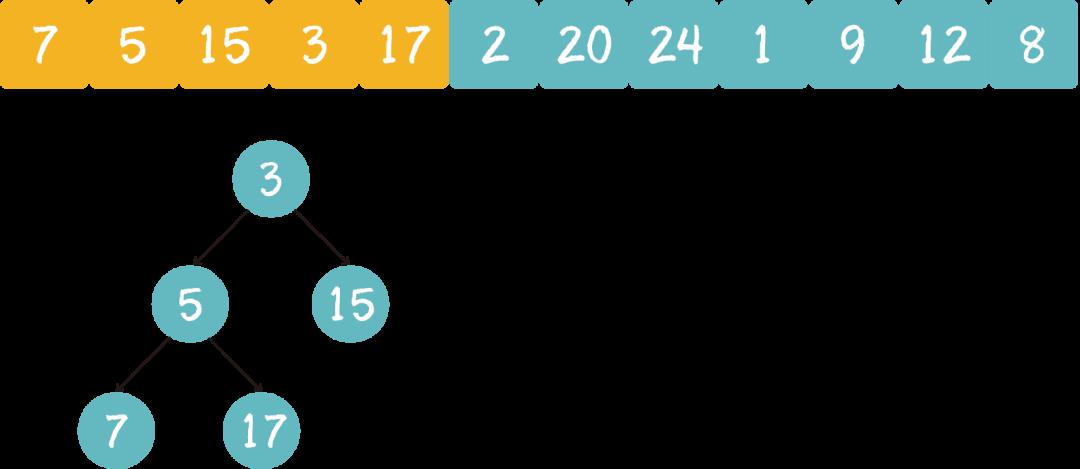
2. 继续遍历数组，和堆顶比较，如果小于等于堆顶，则继续遍历；如果大于堆顶，则取代堆顶元素并调整堆。

遍历到元素2，由于 2<3，所以继续遍历。

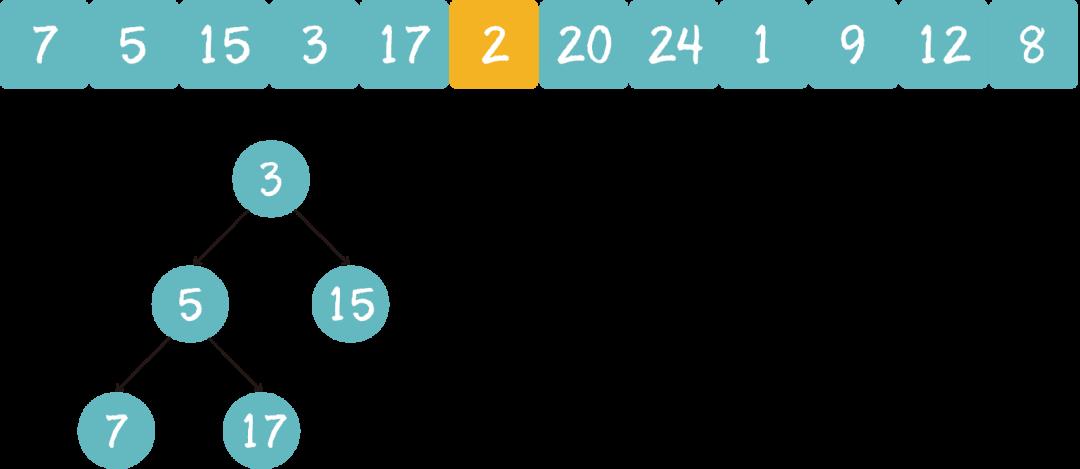
遍历到元素20，由于 20>3，20取代堆顶位置，并调整堆。

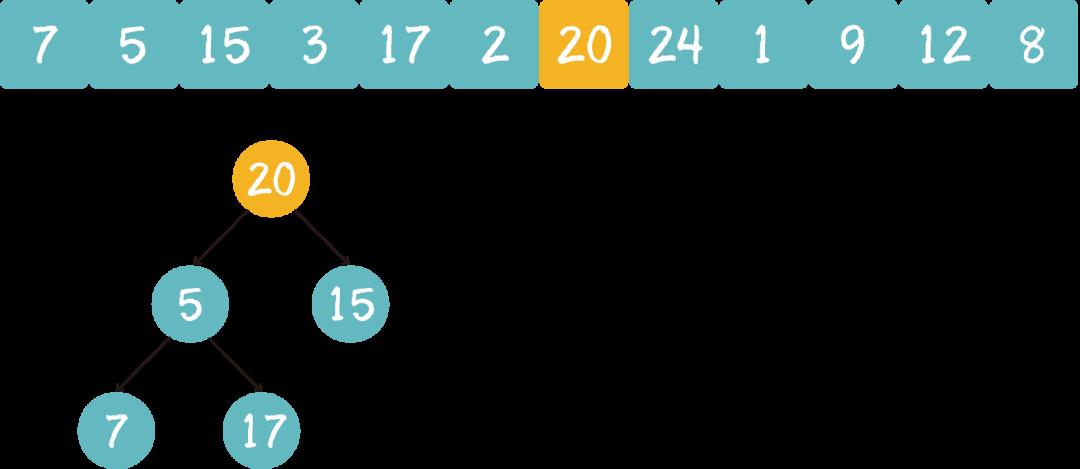
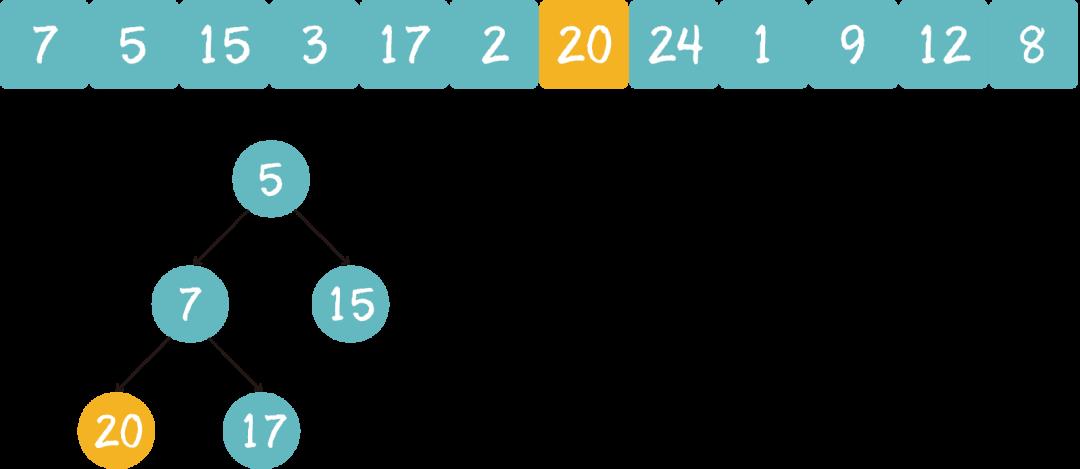
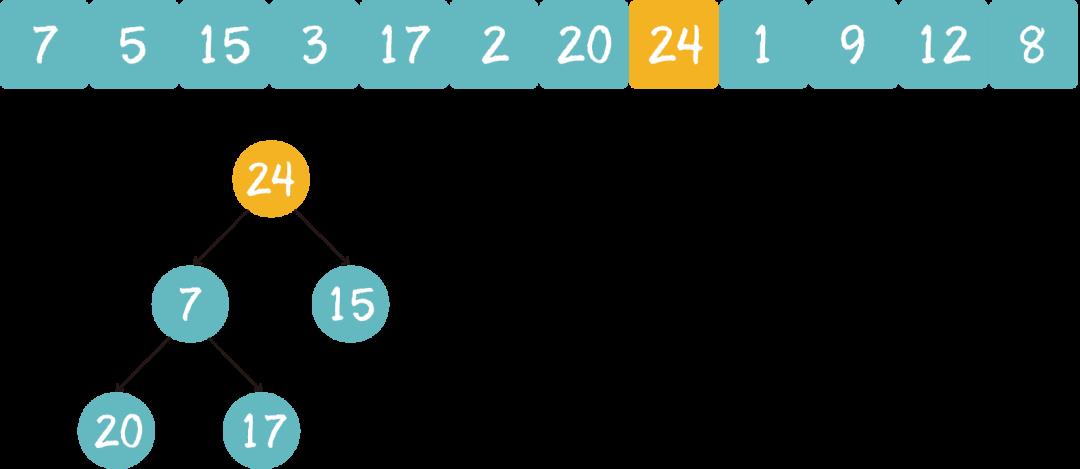
遍历到元素24，由于 24>5，24取代堆顶位置，并调整堆。

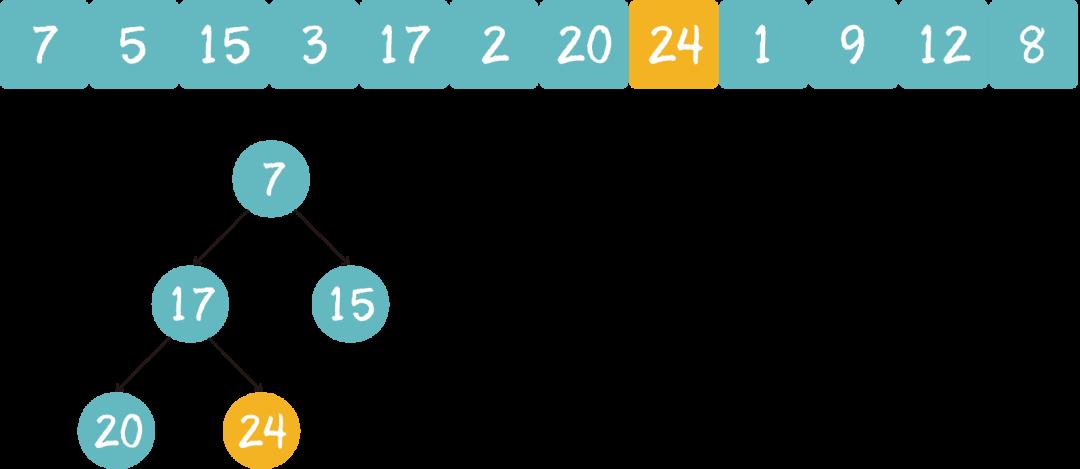
以此类推，我们一个一个遍历元素，当遍历到最后一个元素8的时候，最小堆的情况如下：

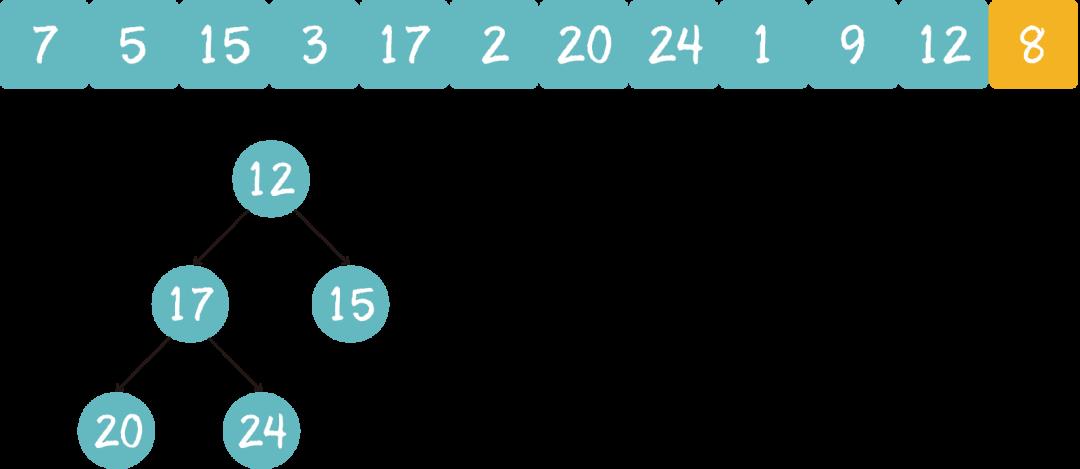
3. 此时的堆顶，就是堆中的最小值，也就是数组中的第k大元素。

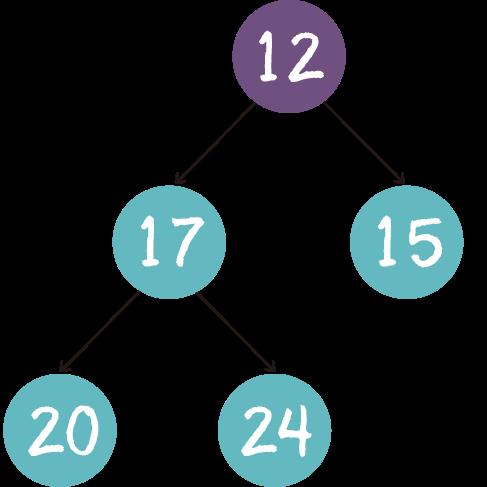
这个方法的时间复杂度是多少呢？

构建堆的时间复杂度是 O（k）
遍历剩余数组的时间复杂度是O（n-k）
每次调整堆的时间复杂度是 O（logk）

其中2和3是嵌套关系，1和2,3是并列关系，所以总的最坏时间复杂度是O（（n-k）logk + k）。当k远小于n的情况下，也可以近似地认为是O（nlogk）。

这个方法的空间复杂度是多少呢？

刚才我们在详细步骤中把二叉堆单独拿出来演示，是为了便于理解。但如果允许改变原数组的话，我们可以把数组的前k个元素“原地交换”来构建成二叉堆，这样就免去了开辟额外的存储空间。

因此，这个方法的空间复杂度是O（1）。

明白了，最小堆法还真是个巧妙的解决方法！怎么用代码来实现呢？

代码很简单，让我们来看一看：

public class KthLargestNumber {    /**     * 寻找第k大的元素     * @param array  待调整的堆     * @param k  第几大     */    public static int findKthLargestNumber(int[] array, int k) {        //1.用前k个元素构建最小堆        buildHeap(array, k);        //2.继续遍历数组，和堆顶比较        for (int i = k; i < array.length; i++) {            if (array[i] > array[0]) {                array[0] = array[i];
                downAdjust(array, 0, k);            }        }        //3.返回堆顶元素        return array[0];    }
    /**     * 构建堆     * @param array  待调整的堆     * @param length  堆的有效大小     */    private static void buildHeap(int[] array, int length) {        // 从最后一个非叶子结点开始，依次下沉调整        for (int i = (length - 2) / 2; i >= 0; i--) {            downAdjust(array, i, length);        }    }
    /**     * 下沉调整     * @param array     待调整的堆     * @param index    要下沉的结点     * @param length    堆的有效大小     */    private static void downAdjust(int[] array, int index, int length) {        // temp保存父结点值，用于最后的赋值        int temp = array[index];        int childIndex = (2 * index) + 1;
        while (childIndex < length) {            // 如果有右孩子，且右孩子小于左孩子的值，则定位到右孩子            if (((childIndex + 1) < length) &&                    (array[childIndex + 1] < array[childIndex])) {                childIndex++;            }            // 如果父结点小于任何一个孩子的值，直接跳出            if (temp <= array[childIndex]) {
                break;            }            //无需真正交换，单向赋值即可            array[index] = array[childIndex];            index = childIndex;            childIndex = (2 * childIndex) + 1;        }
        array[index] = temp;    }
    public static void main(String[] args) {        int[] array = new int[] { 7, 5, 15, 3, 17, 2, 20, 24, 1, 9, 12, 8 };        System.out.println(findKthLargestNumber(array, 5));    }}

原来如此，这下彻底明白啦！

要寻找数组的第k大元素，其实还有一种方法，这种方法就是分治法

方法4：分治法

大家都了解快速排序，快速排序利用分治法，每一次把数组分成较大和较小的两部分。

我们在寻找第k大元素的时候，也可以利用这个思路，以某个元素a为基准，把大于a的元素都交换到数组左边，小于a的元素都交换到数组右边。

比如我们选择以元素7作为基准，把数组分成了左侧较大，右侧较小的两个区域，交换结果如下：