[蓝桥杯]格子刷漆

Posted 2021-06-29 @书生

问题描述：

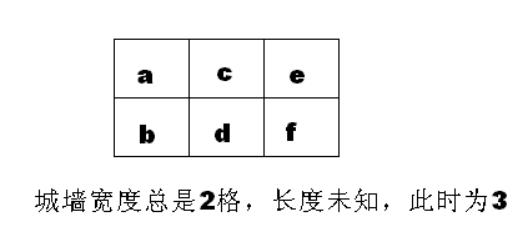
　　X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形（如下图所示），现需要把这些格子刷上保护漆。
 

　　你可以从任意一个格子刷起，刷完一格，可以移动到和它相邻的格子（对角相邻也算数），但不能移动到较远的格子（因为油漆未干不能踩！）
　　比如：a d b c e f 就是合格的刷漆顺序。
　　c e f d a b 是另一种合适的方案。
　　当已知 N 时，求总的方案数。当N较大时，结果会迅速增大，请把结果对 1000000007 (十亿零七) 取模。

链接：http://lx.lanqiao.cn/problem.page?gpid=T38

思路：

本题主要是寻找遍历的方案数量，我们可以采用回溯的方式进行，但是如果N比较大的时候，回溯算法所花费的时间较长，所以本体我们不适用回溯算法，而是使用动态规划。

而使用动态规划，状态定义其实是不容易想到的：

dp1[n] : 表示n列刷漆的方案数(从一个顶点出发，终点任意的刷漆方案数)

dp2[n]: 表示n列刷漆时，起点和终点全在第n列的方案数(单保存了从一个顶点出发)

 以N=2为例，了解状态定义：

以顶点a作为起点：

dp1[2] =6(图1，2，3，4，5，6)  dp2[2]=2 (图3,6)

状态转移：

1. 先刷完第i列再去刷前i-1列

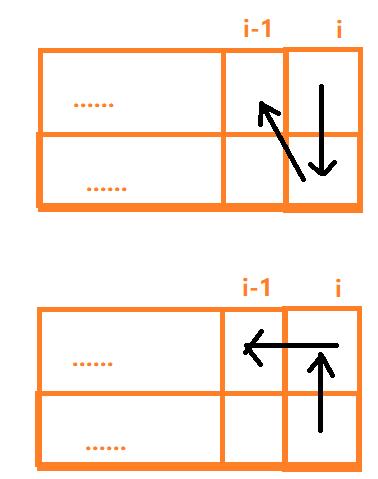
如果采用这种刷漆方法，那么方案数就是dp1[i-1]*2

2.终点和起点全部在第i列的情况

在计算此类方案数的时候，我们需要借助dp2，如果使用dp1必定会踩未干的油漆，导致错误

如果采用这种刷漆方法，那么方案数就是dp2[i-1]*2

3.先刷完第i-1列和第i列，再去刷前i-2列

前两种情况都比较容易思考到，而这种情况是比较难以想到的

如果采用这种刷漆方法，那么方案数就是dp1[i-2]*4

我们通过图解分析出了上面的三种情况，但是仔细观察上面的三种情况都是通过以顶点作为出发点进行实现的，如果我们不适用顶点作为出发点呢

我们从蓝色列开始刷漆的话，分为了左右两个部分，无论我们是先刷完左侧还是先刷完右侧，先刷完的那部分必须能够回到蓝色列，后刷的那部分没有要求

我们可以先刷左侧，再刷右侧 方案数 4*(dp2[i] +dp1[n-i])

               先刷右侧，再刷左侧 方案数 4*(dp2[n-1-i] + dp1[i-1])        

综上:

从顶点出发:

1. 先刷完第i列再去刷前i-1列

dp1[i-1]*2

2.终点和起点全部在第i列的情况

dp2[i-1]*2

3.先刷完第i-1列和第i列，再去刷前i-2列

dp1[i-2]*4

则:dp[i] =dp1[i-1]*2 + dp2[i-1]*2 + dp1[i-2]*4

从非顶点出发

先刷左侧，再刷右侧 方案数 4*(dp2[i] +dp1[n-i])

先刷右侧，再刷左侧 方案数 4*(dp2[n-1-i] + dp1[i-1])     

 

二种总和就是全部方案数：

代码:

#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#include<map>
using namespace std;



#define mod 1000000007;


int main()
{
	int N;
	while(cin>>N)
	{
		if(N==1)
		  {
		  	cout<<2<<endl;
		  	continue;
		  }
		vector<long long> dp1(N+1,0);
		vector<long long> dp2(N+1,0);
		//dp1表示从一点出发，终点是任意的 
		//dp2表示从一点出发，终点与起点是同一列的
		dp2[1]=1;
		dp2[2]=2;

		dp1[1]=1;
		dp1[2]=6;
		for(int i=3;i<=N;++i)
		{
			dp2[i]=(2*dp2[i-1])%mod;
			dp1[i]=(2*dp1[i-1]+4*dp1[i-2]+dp2[i])%mod;
		} 
        //dp[N]只记录了从一个顶点出发的情况，实际中可从四个顶点出发，故乘以4
		long long sum=4*dp1[N]%mod;
		for(int i=2;i<N;i++){
		sum=(sum+4*(dp2[i]*dp1[N-i]+dp2[N-i+1]*dp1[i-1]))%mod;
	}
	cout<<sum<<endl;
	}
	return 0;
}

 参考博客：https://blog.csdn.net/xyf0209/article/details/106810808

 注：如果本篇博客有任何错误和建议，欢迎伙伴们留言，你快说句话啊！